
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 44. Выужденные колебания. Диифференц ур-е и его решение. Резонанс и его условия.Содержание книги
Поиск на нашем сайте
Вынужденные колебания – это колебания, которые происходят под действием внешней периодически изменяющейся силы. Работа вынужденной силы возмещает потерю энергии на трении.
Решением такого Д/У является сумма двух слагаемых,первое из которых характеризует свободные затухающие колебания,а второе – вынужденные колебания.
Со временем первое слагаемое исчезнет и останется только вынужденные колебания с частотой вынужденной силы.
Резонансом называется явление резкого возрастания амплитуды вынужденных колебаний при совпадении частоты вынуждающей силы под действием которой происходит колебания к частоте собственных колебаний колебательной системы. При резонансе амплитуда достигает максимальное значение, а значит частота вынуждающей силы, при которой наступает резонанс получила название резонансной частоты. Резонансная частота: называется амплитудно-резонансной кривой. В зависимости от коэффициента затухания вид кривой меняется. С явлением резонанса приходится считаться при конструировании машин и различного рода сооружений. Собственная частота этих устройств ни в коем случае не должна быть близка к частоте возможных внешних воздействий.
Вопрос 45. Сложение гармонических колебаний,направленных вдоль одной прямой. Биения. Сложение взаимно перпендикулярных колебаний. Поляризованные колебания Выделим два характерных случая:1) Если разность начальных фаз Рассмотрим сложение взаимно перпендикулярных колебаний на примере механических колебаний. Допустим, что материальная точка может совершать колебания как вдоль оси Оx, так и вдоль перпендикулярной к ней оси Оy. Если возбудить оба колебания, материальная точка будет двигаться по некоторой, вообще говоря, криволинейной траектории, форма которой зависит от разности фаз обоих колебаний. Выберем начало отсчета времени так, чтобы начальная фаза первого колебания была равна 0. Тогда уравнения колебаний запишутся следующим образом: исключить из уравнений время. Из первого уравнения (1) следует, что поэтому Уравнение (4) это уравнение эллипса, оси которого повернуты относительно координатных осей Ox и Oy. Ориентация эллипса и величина его полуосей зависят довольно сложным образом от амплитуд A и B и разности фаз Определим форму траектории для некоторых частных случаев.1. Разность фаз равна нулю. В этом случае уравнение (4) примет вид:
Результирующее движение является гармоническим колебанием 2. Разность фаз равна
Движения, описываемые формулами (5) и (6) называют линейно поляризованными колебаниями.
3. При разности фаз равной ±p/2 уравнение (6.5.4) переходит в следующее Вопрос 46. Образование вол в упругой среде. Продольные и поперечные волны. Уравнение плоской волны. Фазовая скорость. Принцип суперпозиции. Стоячие волны. Если частицу упругой среды привести в колебательную систему то вследствии упругой связи она вовлечет в это колебательное движение соседнюю частицу. Эти соседние частицы в свою очередь воздействуют на соседние с ними и так далее. и колебания таким образом начнут распространяться в среде. Процесс распространения колебательного движения в среде называется волновым движением или волной. Волны делятся на: 1)продольные; 2)поперечные. Если каждая частица среды колебаний направлена перпендикулярно распространению волны – это поперечные волны. Если каждая частица среды колебаний распространяется в направлении волны то такая волна называется продольной. В поперечных волнах частица среды в направление распространения волны не перемещается. Колебания каждой последующей точки среды запаздывает по фазе относительно колебаний предыдущей точки. Гребни и впадины перемещаются вдоль направления волны. Скорость с которой в среде распространяются одинаковые фазы колебаний называется фазовой скоростью Уравнение стоячей волны можно получить сложением уравнения падающей волны Это уравнение стоячей волны определяет смещение любой точки волны.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 308; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.107.223 (0.006 с.) |

 - при наличии затухания. График зависимости амплитуды вынужденных колебаний от частоты вынужденной силы
- при наличии затухания. График зависимости амплитуды вынужденных колебаний от частоты вынужденной силы направления; сложение взаимно перпендикулярных колебаний.. Рассмотрим первый случай – сложение двух гармонических колебаний одинакового направления и частоты. Для сложения колебаний удобно применять метод векторных диаграмм. Суть этого метода в том, что гармоническое колебание представляется при помощи вектора, длина которого равна амплитуде колебания, а направление вектора образует с осью OX угол, равный фазе колебания. Амплитуда и начальная фаза результирующего колебания определяются при помощи векторного сложения. Допустим, что требуется сложить два гармонических колебания:
направления; сложение взаимно перпендикулярных колебаний.. Рассмотрим первый случай – сложение двух гармонических колебаний одинакового направления и частоты. Для сложения колебаний удобно применять метод векторных диаграмм. Суть этого метода в том, что гармоническое колебание представляется при помощи вектора, длина которого равна амплитуде колебания, а направление вектора образует с осью OX угол, равный фазе колебания. Амплитуда и начальная фаза результирующего колебания определяются при помощи векторного сложения. Допустим, что требуется сложить два гармонических колебания: 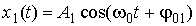 и
и 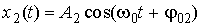 . Сложим соответствующие им векторы
. Сложим соответствующие им векторы  и
и  для момента времени t. Проекция результирующего вектора
для момента времени t. Проекция результирующего вектора  на ось О x равна сумме проекций складываемых векторов
на ось О x равна сумме проекций складываемых векторов 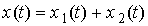 . Вектор
. Вектор 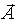 представляет собойвекторное изображение результирующего колебания. Этот вектор в плоскости диаграммы вращается с той же частотой
представляет собойвекторное изображение результирующего колебания. Этот вектор в плоскости диаграммы вращается с той же частотой 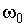 , с которой колеблются складываемые осциллирующие функции x 1(t) и x 2(t). Результирующая амплитуда
, с которой колеблются складываемые осциллирующие функции x 1(t) и x 2(t). Результирующая амплитуда 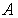 и начальная фаза
и начальная фаза  находятся геометрическим построением для момента времени t =0:
находятся геометрическим построением для момента времени t =0:
 .
.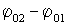 обоих колебаний равна 0 или 2pn, где n=1,2,…. то колебания находятся в фазе и амплитуда результирующего колебания равна сумме амплитуд складываемых колебаний,
обоих колебаний равна 0 или 2pn, где n=1,2,…. то колебания находятся в фазе и амплитуда результирующего колебания равна сумме амплитуд складываемых колебаний,  ; 2) Если разность фаз равно нечетному числу
; 2) Если разность фаз равно нечетному числу  , то
, то  (при
(при  наблюдается полное гашение колебаний).Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами, называются биениями. сложение взаимно перпендикулярных колебаний.
наблюдается полное гашение колебаний).Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами, называются биениями. сложение взаимно перпендикулярных колебаний. и
и  .(1)
.(1) – разность начальных фаз обоих колебаний. Выражения представляют собой заданное в параметрической форме уравнение траектории, по которой движется тело, участвующее в обоих колебаниях. Чтобы получить уравнение траектории в обычном виде, нужно
– разность начальных фаз обоих колебаний. Выражения представляют собой заданное в параметрической форме уравнение траектории, по которой движется тело, участвующее в обоих колебаниях. Чтобы получить уравнение траектории в обычном виде, нужно (2)
(2) (3). Представим далее косинус во втором уравнении (1) по формуле для косинуса суммы, подставляя при этом вместо
(3). Представим далее косинус во втором уравнении (1) по формуле для косинуса суммы, подставляя при этом вместо  и
и  их значения из соотношений (2) и (3). В результате
их значения из соотношений (2) и (3). В результате  (4)
(4)

 (5)
(5) вдоль этой прямой с частотой
вдоль этой прямой с частотой 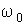 и амплитудой равной
и амплитудой равной 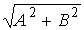 .
. . В этом случае уравнение (4) примет вид:
. В этом случае уравнение (4) примет вид: 
 Откуда получается, что результирующее движение представляет собой гармоническое колебание вдоль прямой:
Откуда получается, что результирующее движение представляет собой гармоническое колебание вдоль прямой:  (6)
(6)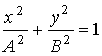 , т.е. в уравнение эллипса, приведенного к координатным осям, причем полуоси эллипса равны соответствующим амплитудам колебаний A и B. В этом случае говорят об эллиптически поляризованных колебаниях. При равенстве амплитуд (A=B) эллипс превращается в окружность. Колебания, описываемые уравнением при (A=B) называются поляризованными по кругу или циркулярно поляризованными. Случаи разности фаз +p/2 и -p/2 отличаются направлением движения по эллипсу или по окружности. В первом случае тело движется по часовой стрелке, во втором – против часовой стрелки.
, т.е. в уравнение эллипса, приведенного к координатным осям, причем полуоси эллипса равны соответствующим амплитудам колебаний A и B. В этом случае говорят об эллиптически поляризованных колебаниях. При равенстве амплитуд (A=B) эллипс превращается в окружность. Колебания, описываемые уравнением при (A=B) называются поляризованными по кругу или циркулярно поляризованными. Случаи разности фаз +p/2 и -p/2 отличаются направлением движения по эллипсу или по окружности. В первом случае тело движется по часовой стрелке, во втором – против часовой стрелки. . Поверхности образованные точками с одинаковыми фазами называются поверхностями одинаковых фаз или волновыми поверхностями. Если поверхности одинаковых фаз представляют собой плоскости параллельные друг другу то это плоские волны. Уравнение плоской волны:
. Поверхности образованные точками с одинаковыми фазами называются поверхностями одинаковых фаз или волновыми поверхностями. Если поверхности одинаковых фаз представляют собой плоскости параллельные друг другу то это плоские волны. Уравнение плоской волны:  - общее уравнение плоской бегущей волны, оно указывает смещение точки среды в момент времени t у которых координата х.
- общее уравнение плоской бегущей волны, оно указывает смещение точки среды в момент времени t у которых координата х.  - волновое число,тогда
- волновое число,тогда 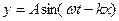 .Физический смысл волнового числа: Волновое число показывает сколько одинаковых волн укладывается на отрезке длиной 2пи метра. Если в среде распространяются одновременно несколько волн, то колебания частиц среды оказываются геометрической суммой колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности. Следовательно, волны просто накладываются одна на другую, не возмущая друг друга. Это утверждение называется принципом суперпозиции волн. Принцип суперпозиции утверждает, что движение, вызванное распространением сразу нескольких волн, есть снова некоторый волновой процесс. Таким процессом, например, является звучание оркестра. Оно возникает от одновременного возбуждения звуковых колебаний воздуха отдельными музыкальными инструментами. Замечательно, что при наложении волн могут возникать особые явления. Их называют эффектами сложения или, как еще говорят, суперпозиции волн. Стоя́чая волна́ — колебания в распределённых колебательных системах с характерным расположением чередующихся максимумов (пучностей) и минимумов (узлов) амплитуды. Практически такая волна возникает при отражениях от преград и неоднородностей в результате наложения отражённой волны на падающую. При этом крайне важное значение имеет частота, фаза и коэффициент затухания волны в месте отражения.
.Физический смысл волнового числа: Волновое число показывает сколько одинаковых волн укладывается на отрезке длиной 2пи метра. Если в среде распространяются одновременно несколько волн, то колебания частиц среды оказываются геометрической суммой колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности. Следовательно, волны просто накладываются одна на другую, не возмущая друг друга. Это утверждение называется принципом суперпозиции волн. Принцип суперпозиции утверждает, что движение, вызванное распространением сразу нескольких волн, есть снова некоторый волновой процесс. Таким процессом, например, является звучание оркестра. Оно возникает от одновременного возбуждения звуковых колебаний воздуха отдельными музыкальными инструментами. Замечательно, что при наложении волн могут возникать особые явления. Их называют эффектами сложения или, как еще говорят, суперпозиции волн. Стоя́чая волна́ — колебания в распределённых колебательных системах с характерным расположением чередующихся максимумов (пучностей) и минимумов (узлов) амплитуды. Практически такая волна возникает при отражениях от преград и неоднородностей в результате наложения отражённой волны на падающую. При этом крайне важное значение имеет частота, фаза и коэффициент затухания волны в месте отражения. 
 и уравнения отраженной волны
и уравнения отраженной волны  .
.



