
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 38. Уравнение ван-дер-ваальса и сопоставление его с опытом. Критическое состояние. Связь между критическими параметрами. Внутренняя энергия реального газа.Содержание книги
Поиск на нашем сайте
Используя модель голландского ученого Ван-дер-Ваальс предложил уравнение состояния для 1 моля реального газа которое носи его имя.
Это уравнение лучше описывает состояние газа чем уравнение Клайперона. а = (27· R2 ·Т2к)/(64 ·Pк); b = (27· R ·Тк)/(8 ·Pк). Внутренняя энергия реального газа складывается из кинетической энергии теплового движения его молекул (определяет внутреннюю энергию идеального газа, равную CVT) и потенциальной энергии межмолекулярного взаимодействия. Потенциальная энергия реального газа обусловлена только силами притяжения между молекулами. Наличие сил притяжения приводит к возникновению внутреннего давления на газ p'=a/V 2m. Работа, которая затрачивается для преодоления сил притяжения, действующих между молекулами газа, как известно из механики, идет на увеличение потенциальной энергии системы, т. е. d A=p'dVm=d П, или dП=(a/V2m)dVm, откуда П =-a/Vm (постоянная интегрирования принята равной нулю). Знак минус означает, что молекулярные силы, создающие внутреннее давление р', являются силами притяжения. Учитывая оба слагаемых, получим, что внутренняя энергия моля реального газа Um = CVT-a/Vm -растет с повышением температуры и увеличением объема. Если газ расширяется без теплообмена с окружающей средой (адиабатический процесс, т. е. d Q = 0) и не совершает внешней работы (расширение газа в вакуум, т. е. dA=0), то на основании первого начала термодинамики (dQ=(U2-U1 )+dA) получим, что U 1 =U2. Следовательно, при адиабатическом расширении без совершения внешней работы внутренняя энергия газа не изменяется. Равенство формально справедливо как для идеального, так и для реального газов, но физически для обоих случаев совершенно различно. Для идеального газа равенство U 1 =U 2означает равенство температур (Т 1 =Т 2 ), т. е. при адиабатическом расширении идеального газа в вакуум его температура не изменяется. Для реального газа из равенства, учитывая, что для моля газа U 1 =CVT 1 -a/V1, U 2 =CVT 2 -a/V 2. Так как V 2 >V 1, то Т 1 >Т 2, т. е. реальный газ при адиабатическом расширении в вакуум охлаждается. При адиабатическом сжатии реальный газ нагревается.
Вопрос 39. Эффект джоуля томсона. Температура инверсии. Сжатие газов.
Вопрос 40. Колебания и характеризующие их величины. Собственные колебания. Свободными (собственными) колебаниями называются колебания, которые происходят в отсутствии переменных внешних воздействий на колебательную систему и возникают вследствие какого-либо начального отклонения этой системы от состояния устойчивого равновесия; колебания, которые совершаются за счёт первоначально сообщённой энергии при последующем отсутствии внешних воздействий на колебательную систему. Вынужденные колебания – это колебания которые происходят под действием внешней периодически изменяющийся силы. Гармонические колебания – колебания, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса. Уравнение гармонических колебаний колебательной величины s: s=Acos(ω0t+φ) или s=Asin(ω0t+φ), где A – амплитуда колебаний, ω0 – круговая (циклическая) частота, φ – начальная фаза колебаний в момент времени t=0, (ω0t+φ) – фаза колебаний в момент времени t. Период гармонического колебания – промежуток времени T, в течение которого фаза колебания получает приращение 2π, т.е. ω0(t+T)+φ=(ω0t+φ)+2π. T=2π/ω0. Период колебаний - наименьший промежуток времени, по истечении которого система, совершающая колебания, снова возвращается в то же состояние, в котором она находилась в начальный произвольно выбранный момент. T=t/N=1/v=2π/ω. Частота колебаний – число полных колебаний, совершаемых в единицу времени. ν=1/T=N/t= ω/2π. Циклическая частота ω(рад/с) – число колебаний за 2π с. ω= 2πv= 2π/T. Амплитуда колебаний – это максимальное значение колеблющейся величины. Фаза колебаний – это значение колеблющейся величины в произвольный момент времени (ω0t+φ). Проекции скорости и ускорения колебательной точки:
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 568; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.218.234 (0.008 с.) |


 - поправка на силы взаимодействия. b-поправка на собственное размножение молекул.
- поправка на силы взаимодействия. b-поправка на собственное размножение молекул. . Для исследования поведения реального газа рассмотрим изотермы Ван-дер-Ваальса — кривые зависимости р от V m при заданных Т, определяемые уравнением Ван-дер-Ваальса для моля газа. Эти кривые рассматриваются для четырех различных температур; имеют довольно своеобразный характер. При высоких температурах (T > T к) изотерма реального газа отличается от изотермы идеального газа только некоторым искажением ее формы, оставаясь монотонно спадающей кривой. При некоторой температуре T к на изотерме имеется лишь одна точка перегиба К.
. Для исследования поведения реального газа рассмотрим изотермы Ван-дер-Ваальса — кривые зависимости р от V m при заданных Т, определяемые уравнением Ван-дер-Ваальса для моля газа. Эти кривые рассматриваются для четырех различных температур; имеют довольно своеобразный характер. При высоких температурах (T > T к) изотерма реального газа отличается от изотермы идеального газа только некоторым искажением ее формы, оставаясь монотонно спадающей кривой. При некоторой температуре T к на изотерме имеется лишь одна точка перегиба К. Эта изотерма называется критической, соответствующая ей температура T к — критической температурой; точка перегиба К называется критической точкой; в этой точке касательная к ней параллельна оси абсцисс. Соответствующие этой точке объем V к, и давление р к называются также критическими. Состояние с критическими параметрами (p к, V к, T к) называется критическим состоянием. При низких температурах (Т < T к) изотермы имеют волнообразный участок, сначала монотонно опускаясь вниз, затем монотонно поднимаясь вверх и снова монотонно опускаясь.Для пояснения характера изотерм преобразуем уравнение Ван-дер-Ваальса к виду
Эта изотерма называется критической, соответствующая ей температура T к — критической температурой; точка перегиба К называется критической точкой; в этой точке касательная к ней параллельна оси абсцисс. Соответствующие этой точке объем V к, и давление р к называются также критическими. Состояние с критическими параметрами (p к, V к, T к) называется критическим состоянием. При низких температурах (Т < T к) изотермы имеют волнообразный участок, сначала монотонно опускаясь вниз, затем монотонно поднимаясь вверх и снова монотонно опускаясь.Для пояснения характера изотерм преобразуем уравнение Ван-дер-Ваальса к виду  ЭтоУравнение при заданных р и Т является уравнением третьей степени относительно V m; следовательно, оно может иметь либо три вещественных корня, либо один вещественный и два мнимых, причем физический смысл имеют лишь вещественные положительные корни. Поэтому первому случаю соответствуют изотермы при низких температурах (три значения объема газа V 1, V 2 и V 3 отвечают (символ «m» для простоты опускаем) одному значению давления р 1), второму случаю — изотермы при высоких температурах.
ЭтоУравнение при заданных р и Т является уравнением третьей степени относительно V m; следовательно, оно может иметь либо три вещественных корня, либо один вещественный и два мнимых, причем физический смысл имеют лишь вещественные положительные корни. Поэтому первому случаю соответствуют изотермы при низких температурах (три значения объема газа V 1, V 2 и V 3 отвечают (символ «m» для простоты опускаем) одному значению давления р 1), второму случаю — изотермы при высоких температурах. 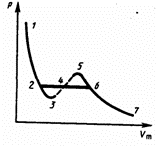 Рассматривая различные участки изотермы при T < Т к, видим, что на участках 1 — 3 и 5 — 7 при уменьшении объема V m давление р возрастает, что естественно. На участке 3—5 сжатие вещества приводит к уменьшению давления; практика же показывает, что такие состояния в природе не осуществляются. Наличие участка 3—5 означает, что при постепенном изменении объема вещество не может оставаться все время в виде однородной среды; в некоторый момент должно наступить скачкообразное изменение состояния и распад вещества на две фазы. Таким образом, истинная изотерма будет иметь вид ломаной линии 7 — 6—2—1. Часть 6–7 отвечает газообразному состоянию, а часть 2 – 1 — жидкому. В состояниях, соответствующих горизонтальному участку изотермы 6—2, наблюдается равновесие жидкой и газообразной фаз вещества. Вещество в газообразном состоянии при температуре ниже критической называется паром, а пар, находящийся в равновесии со своей жидкостью, называется насыщенным. Критическими параметрами газа называются значения его макропараметров (давления, объёма и температуры) в критической точке, т.е. в таком состоянии, когда жидкая и газообразная фазы вещества неразличимы.Связь между критическими параметрами и постоянными уравнения Ван-дер-Ваальса: Тк = 8·а/(27·R·b); Pк = a/(27·b2);
Рассматривая различные участки изотермы при T < Т к, видим, что на участках 1 — 3 и 5 — 7 при уменьшении объема V m давление р возрастает, что естественно. На участке 3—5 сжатие вещества приводит к уменьшению давления; практика же показывает, что такие состояния в природе не осуществляются. Наличие участка 3—5 означает, что при постепенном изменении объема вещество не может оставаться все время в виде однородной среды; в некоторый момент должно наступить скачкообразное изменение состояния и распад вещества на две фазы. Таким образом, истинная изотерма будет иметь вид ломаной линии 7 — 6—2—1. Часть 6–7 отвечает газообразному состоянию, а часть 2 – 1 — жидкому. В состояниях, соответствующих горизонтальному участку изотермы 6—2, наблюдается равновесие жидкой и газообразной фаз вещества. Вещество в газообразном состоянии при температуре ниже критической называется паром, а пар, находящийся в равновесии со своей жидкостью, называется насыщенным. Критическими параметрами газа называются значения его макропараметров (давления, объёма и температуры) в критической точке, т.е. в таком состоянии, когда жидкая и газообразная фазы вещества неразличимы.Связь между критическими параметрами и постоянными уравнения Ван-дер-Ваальса: Тк = 8·а/(27·R·b); Pк = a/(27·b2); В теплоизолированной трубке с пористой перегородкой находится два поршня, которые могут перемещаться без трения. Пусть сначала слева от перегородки газ под поршнем 1 находится под давлением р1, занимает объем V1 при температуре Т1, а справа газ отсутствует (поршень 2 придвинут к перегородке). После прохождения газа через пористую перегородку в правой части газ характеризуется параметрами р2, V2, Т2. Давления р1 и р2 поддерживаются постоянными (р1>р2). Так как расширение газа происходит без теплообмена с окружающей средой (адиабатически), то на основании первого начала термодинамики dQ=(U2-U1)+dA=0. Внешняя работа, совершаемая газом, состоит из положительной работы при движении поршня 2 (A2=p2V2) и отрицательной при движении поршня 1 (A1=p1V1), т.е. dA=A2-А1, получим U1+p1V1=U2+p2V2. Таким образом, в опыте Джоуля — Томсона сохраняется (остается неизменной) величина U+pV. Она является функцией состояния и называется энтальпией. Изменение температуры реального газа в результате его адиабатического расширения — медленного прохождения газа под действием перепада давления сквозь дроссель(например, пористую перегородку), называется эффектом Джоуля — Томсона. Эффект Джоуля — Томсона принято называть положительным, если газ в процессе дросселирования охлаждается (DT<0), и отрицательным, если газ нагревается (DT>0). В зависимости от условий дросселирования для одного и того же газа эффект Джоуля — Томсона может быть как положительным, так и отрицательным. Температура, при которой (для данного давления) происходит изменение знака эффекта Джоуля — Томсона, называется температурой инверсии
В теплоизолированной трубке с пористой перегородкой находится два поршня, которые могут перемещаться без трения. Пусть сначала слева от перегородки газ под поршнем 1 находится под давлением р1, занимает объем V1 при температуре Т1, а справа газ отсутствует (поршень 2 придвинут к перегородке). После прохождения газа через пористую перегородку в правой части газ характеризуется параметрами р2, V2, Т2. Давления р1 и р2 поддерживаются постоянными (р1>р2). Так как расширение газа происходит без теплообмена с окружающей средой (адиабатически), то на основании первого начала термодинамики dQ=(U2-U1)+dA=0. Внешняя работа, совершаемая газом, состоит из положительной работы при движении поршня 2 (A2=p2V2) и отрицательной при движении поршня 1 (A1=p1V1), т.е. dA=A2-А1, получим U1+p1V1=U2+p2V2. Таким образом, в опыте Джоуля — Томсона сохраняется (остается неизменной) величина U+pV. Она является функцией состояния и называется энтальпией. Изменение температуры реального газа в результате его адиабатического расширения — медленного прохождения газа под действием перепада давления сквозь дроссель(например, пористую перегородку), называется эффектом Джоуля — Томсона. Эффект Джоуля — Томсона принято называть положительным, если газ в процессе дросселирования охлаждается (DT<0), и отрицательным, если газ нагревается (DT>0). В зависимости от условий дросселирования для одного и того же газа эффект Джоуля — Томсона может быть как положительным, так и отрицательным. Температура, при которой (для данного давления) происходит изменение знака эффекта Джоуля — Томсона, называется температурой инверсии 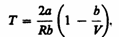 .Эффект Джоуля — Томсона обусловлен отклонением газа от идеальности. В самом деле, для моля идеального газа Vm = RT, поэтому выражение примет вид CVT1+RT1=CVT2 + RT2, откуда следует, что T1=T2. Превращение любого газа в жидкость — сжижение газа — возможно лишь при температуре ниже критической. При ранних попытках сжижения газов оказалось, что некоторые газы (Сl2, СО2, NН3) легко сжижались изотермическим сжатием, а целый ряд газов (О2, n2, Н2, Не) сжижению не поддавался. Впоследствии удалось получить жидкий кислород, азот и водород (их критические температуры равны соответственно 154,4, 126,1 и 33 К), а в 1908 г. нидерландский физик Г. Камерлинг-Оннес (1853—1926) добился сжижения гелия, имеющего самую низкую критическую температуру (5,3 К). Для сжижения газов чаще применяются два промышленных метода, в основе которых используется либо эффект Джоуля — Томсона, либо охлаждение газа при совершении им работы. Второй метод сжижения газов основан на охлаждении газа при совершении им работы. Сжатый газ, поступая в поршневую машину (детандер), расширяется и совершает при этом работу по передвижению поршня. Так как работа совершается за счет внутренней энергии газа, то его температура при этом понижается.
.Эффект Джоуля — Томсона обусловлен отклонением газа от идеальности. В самом деле, для моля идеального газа Vm = RT, поэтому выражение примет вид CVT1+RT1=CVT2 + RT2, откуда следует, что T1=T2. Превращение любого газа в жидкость — сжижение газа — возможно лишь при температуре ниже критической. При ранних попытках сжижения газов оказалось, что некоторые газы (Сl2, СО2, NН3) легко сжижались изотермическим сжатием, а целый ряд газов (О2, n2, Н2, Не) сжижению не поддавался. Впоследствии удалось получить жидкий кислород, азот и водород (их критические температуры равны соответственно 154,4, 126,1 и 33 К), а в 1908 г. нидерландский физик Г. Камерлинг-Оннес (1853—1926) добился сжижения гелия, имеющего самую низкую критическую температуру (5,3 К). Для сжижения газов чаще применяются два промышленных метода, в основе которых используется либо эффект Джоуля — Томсона, либо охлаждение газа при совершении им работы. Второй метод сжижения газов основан на охлаждении газа при совершении им работы. Сжатый газ, поступая в поршневую машину (детандер), расширяется и совершает при этом работу по передвижению поршня. Так как работа совершается за счет внутренней энергии газа, то его температура при этом понижается. . Свободные колебания в замкнутой консервативной системе называются собственными колебаниями(отсутствие силы сопротивления и трения). Наиболее простым случаем является случай, когда возвращаемая сила пропорциональна отклонению от положения равновесия
. Свободные колебания в замкнутой консервативной системе называются собственными колебаниями(отсутствие силы сопротивления и трения). Наиболее простым случаем является случай, когда возвращаемая сила пропорциональна отклонению от положения равновесия  , где к- коэффициент квази.
, где к- коэффициент квази.


