
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Нелинейные волновые взаимодействияСодержание книги
Поиск на нашем сайте
§18. ГЕНЕРАЦИЯ ОПТИЧЕСКИХ ГАРМОНИК
В настоящее время широкое применение в технике и в научных исследованиях нашли процессы генерации оптических гармоник, преобразование частоты вверх и параметрическая генерация света. В этом параграфе изложена генерация второй гармоники для одномерного случая. Детальное освещение данного вопроса можно найти в монографии [14]. Итак, пусть взаимодействующие монохроматические волны движутся в одном направлении так, что для каждой волны электрическое поле есть функция одной координаты:
где “штрих” – производная по z; “ точка ” – производная по времени. Общее выражение для монохроматических взаимодействующих полей представляется суммой
Для слаболинейных сред можно предполагать медленное изменение амплитуды на длине волны
Здесь
Из (18.3) и (18.4) для прозрачной среды, где
Эти соотношения в теории параметрического усиления (первые интегралы системы (18.3)), которые на языке квантовой физики означают, что изменение интенсивности трехволнового взаимодействия происходит за счет преобразования одного кванта Аналогичная укороченная система уравнений выводится для процесса генерации второй гармоники
где
Перейдем к приближению заданного поля. В ряде случаев преобразование во вторую гармонику невелико:
которое имеет решение в виде двух слагаемых – свободная волна (решение однородного уравнения) и вынужденная. Таким образом, электрическое поле для второй гармоники примет вид
где
Отсюда видно, что амплитуда вынужденной волны (18.10) имеет сложную резонансную зависимость (см. гл. III). На длине В этом случае интенсивность второй гармоники
где
Видно, что при
где
где
§19. ПРОСТРАНСТВЕННЫЙ СИНХРОНИЗМ
Укороченная система уравнений (18.6) и (18.7) имеет точное решение [7]. Из (18.14) видно, что условие
представляет собой особый случай, когда приближение заданного поля будет несправедливо. Это условие означает, что взаимодействующие волны полностью согласованы по фазе, то есть осуществляется пространственный синхронизм, или фазовое согласование. Синхронные согласованные взаимодействия приводят к значительным преобразованиям. Действительно, при условии (19.1) для прозрачной среды укороченная система уравнений принимает вид
где
Введем новые обозначения
Подставляя (19.3) в (19.2), получим уравнения для амплитуд
и для разности фаз
Из последнего уравнения видно, что
Подставляя (19.6) во второе уравнение системы (19.4) и интегрируя последнее, приходим к известному результату
С учетом (19.6) получим
Таким образом, в условиях пространственного синхронизма происходит полное преобразование основного когерентного излучения во вторую гармонику.
§20. РЕЗОНАНСНАЯ ГЕНЕРАЦИЯ ТРЕТЬЕЙ ГАРМОНИКИ
Подобная ситуация создается в случае генерации третьей гармоники. В приближении заданного поля уравнение для третьей гармоники, аналогичное (18.8), представлено в виде
где
где
Отметим, что резонансы
§21. МЕТОДЫ СОЗДАНИЯ ФАЗОВОГО СОГЛАСОВАНИЯ
Условие пространственного синхронизма можно создать несколькими способами. При генерации второй гармоники используют двоякопреломляющие одноосные кристаллы. Одноосный кристалл может быть двух типов: положительный (показатель преломления обыкновенной волны меньше, чем необыкновенной) и отрицательный (показатель преломления обыкновенной волны больше, чем необыкновенной). Для отрицательного кристалла основная волна, поляризованная как обыкновенный луч (то есть плоскость поляризации волны перпендикулярна оси кристалла), синхронизируется со второй гармоникой ( Для положительного кристалла ситуация прямо противоположная: условие пространственной синхронизации выполняется для основной необыкновенной волны и обыкновенной волны второй гармоники. Фазовая синхронизация достигается также путем взаимодействия двух основных волн – обыкновенной и необыкновенной – с одной обыкновенной волной второй гармоники (положительный кристалл) или с одной необыкновенной волной (отрицательный кристалл). Возможны и другие методы создания синхронных взаимодействий. Наиболее выгодным оказывается случай, когда условие При генерации третьей гармоники синхронизация осуществляется иным путем. Необходимо выполнить условие:
(21.1) На этом пути удалось продвинуться в область вакуумного ультрафиолета (
22. ПАРАМЕТРИЧЕСКИЕ ВЗАИМОДЕЙСТВИЯ
Генерация оптических гармоник есть частный случай эффекта смешения частот. В приближении заданного поля легко получить амплитуду поля на суммарной частоте. Для этого предположим, что две волны на частотах
где
Сравнивая (22.1) с (18.8), убедимся, что решение (22.1) будет иметь вид, аналогичный (18.9)
где амплитуда вынужденной волны
что полностью определяет электродинамику малых преобразований эффектов смешивания частот. Эффективность преобразования резко возрастает при условии фазового согласования: Рассмотрим процесс параметрического преобразования частоты вверх, несколько отличающийся от эффекта смешения. Пусть частота
где
Для принятых граничных условий решение уравнений (22.5) выглядит таким образом:
Откуда видно, что волна с частотой Далее обратимся к параметрическому усилению и генерации. Из соотношений Мэнли-Роу (18.5) следует, что фотон наибольшей частоты распадается на два фотона меньшей частоты. Таким образом, слабый сигнал на меньшей частоте может быть усилен за счет энергии волны высокой частоты – волны накачки. Возникающая волна разностной частоты – холостая волна – также будет усиливаться. Если организована обратная связь, например, сигнал повторно пропускается через кристалл в нужной фазе (резонатор), то усилитель превращается в генератор, причем самовозбуждение генератора может произойти с затравкой из шумов, когда усиление за один проход превысит соответствующие потери. Из системы (18.3) следует, что для заданной амплитуды волны накачки
где
где
Общее решение (22.9) при
и аналогичное выражение для
и для холостой волны
В предельном случае (
Отклонение от условий фазового синхронизма (
откуда следует, что существует порог для усиления
Если учесть потери, то в случае их равенства и при
Где
§23. ВЫНУЖДЕННОЕ РАССЕЯНИЕ МАНДЕЛЬШТАМА-БРИЛЛЮЭНА (ВРМБ)
Примером нелинейного взаимодействия волн - электромагнитной и звуковой – является эффект ВРМБ. Известно, что при малых интенсивностях света происходит процесс рассеяния на флуктуациях плотности среды. Элементарный акт рассеяния электромагнитной волны на акустических колебаниях состоит из поглощения фотона, падающего на среду, и из одновременного испуская фотона рассеянного излучения и акустического фонона (стоксово рассеяние). Из законов сохранения энергии и импульса
(23.1)
где
где Аналогичный сдвиг происходит при поглощении падающего фотона и акустического фонона и последующего рождения рассеянного фотона (антистоксово рассеяние). Таким образом, относительно несмещенной частоты рассеянного излучения (рэлеевское рассеяние) возникают две компоненты – дублет Мандельштама-Бриллюэна, а сам эффект носит название – спонтанное Мандельштама-Бриллюэна рассеяние. Заметим, что если аналогичное рассеяние излучения происходит с поглощением или испусканием оптического фонона, то эффект носит название – спонтанное комбинационное (рамановское) рассеяние. При спонтанном рассеянии флуктуации плотности в среде не зависят от проходящей через нее световой волны, что характерно для достаточно малых интенсивностей. Однако положение резко меняется при мощном когерентном излучении. Интерференция мощных световых волн – падающей и рассеянной – вызывает заметный эффект электрострикции, который приводит к усилению звуковых волн, а последние, в свою очередь, влияют на рассеяние излучения. Весь процесс становится нелинейным, а эффект называют – вынужденное рассеяние Мандельштама-Бриллюэна (ВРМБ) Кратко изложим основные результаты использования теории ВРМБ в жидкости. Движение вязкой жидкости описывается уравнением Навье-Стокса:
где
Индекс “0” означает равновесное состояние. Эта сила вызывает изменение плотности среды, с учетом которого волновое уравнение для электромагнитного поля записывается в форме
где
где
Уравнения (23.6) и (23.7) образуют замкнутую систему для электрического поля и давления при акустических колебаниях среды с учетом поглощения. Будем искать решение для падающей и рассеянной световых волн в виде
а звуковую волну запишем так
Предположим, что падающая волна фиксирована по фазе и амплитуде, а для стоксовой и звуковой волн считаем
где введены обозначения
здесь
В общем случае при Вышеприведенный анализ показывает, что рассматриваемая задача взаимодействия световой и звуковой волн в некотором смысле аналогична задаче параметрического усиления. Поэтому должен существовать порог генерации стоксовой и звуковой волн. Последующий анализ можно выполнить по той же методике, что изложена в § 21. Из дидактических соображений приведем этот анализ через укороченную систему уравнений. Покажем это на примере рассеяния назад, когда угол
Допустим, что звуковая волна и волна накачки движутся в отрицательном направлении, тогда связь волновых векторов и частот можно представить в виде
Амплитуды
где введены коэффициенты поглощения. Пусть
подставляя (23.16) в (23.15), получим систему алгебраических уравнений для нахождения
где
причем считаем также, что поле слабое (
возникает усиление, тогда как звуковая волна по-прежнему сильно поглощается.
ПРИЛОЖЕНИЕ
|
||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 300; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.73.117 (0.014 с.) |

 . Положим, что все волны имеют одинаковую поляризацию, причем поле перпендикулярно направлению распространения. Это условие легко выполняется в изотропных средах и кубических кристаллах, однако оно не столь существенно и принято лишь с целью упрощения формул. В одномерном случае уравнение для поля запишется в виде
. Положим, что все волны имеют одинаковую поляризацию, причем поле перпендикулярно направлению распространения. Это условие легко выполняется в изотропных средах и кубических кристаллах, однако оно не столь существенно и принято лишь с целью упрощения формул. В одномерном случае уравнение для поля запишется в виде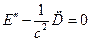 , (18.1)
, (18.1) (18.2)
(18.2) . Если анализ ограничить лишь тремя волнами, для которых
. Если анализ ограничить лишь тремя волнами, для которых 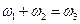 , то из (18.1) и (18.2) можно получить укороченную систему уравнений
, то из (18.1) и (18.2) можно получить укороченную систему уравнений ;
; ;
; . (18.3)
. (18.3) , причем (18.3) справедливо и для поглощающей среды. Для плоской волны
, причем (18.3) справедливо и для поглощающей среды. Для плоской волны  , а вектор Пойнтинга
, а вектор Пойнтинга (18.4)
(18.4) , выводятся соотношения:
, выводятся соотношения: ;
; ;
;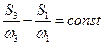 .
. в два
в два  и
и  . Из общей системы (18.3) также следует, что
. Из общей системы (18.3) также следует, что  , то есть это соответствует закону сохранения энергии взаимодействующих полей.
, то есть это соответствует закону сохранения энергии взаимодействующих полей. ; (18.6)
; (18.6) , (18.7)
, (18.7) ;
;  ;
;  .
. . Тогда можно считать поле основной волны заданным, равным входному
. Тогда можно считать поле основной волны заданным, равным входному  . Однако не обязательно считать функцию
. Однако не обязательно считать функцию 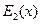 медленно меняющейся. Если оставить и вторые производные, то (18.6) можно заменить уравнением
медленно меняющейся. Если оставить и вторые производные, то (18.6) можно заменить уравнением , (18.8)
, (18.8)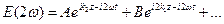 , (18.9)
, (18.9) (18.10)
(18.10)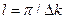 происходит рассогласование фаз свободной и вынужденной волны. Эту длину называют когерентной. Для нулевых граничных условий с (
происходит рассогласование фаз свободной и вынужденной волны. Эту длину называют когерентной. Для нулевых граничных условий с ( при
при  ) получим
) получим 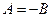 .
. , (18.11)
, (18.11)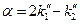 ,
, 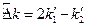 . В прозрачной среде
. В прозрачной среде 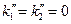 , таким образом, приходим к широко известному в нелинейной оптике результату:
, таким образом, приходим к широко известному в нелинейной оптике результату: . (18.12)
. (18.12) преобразование достигает максимума и равно
преобразование достигает максимума и равно  . Если
. Если  , то можно исходить непосредственно их укороченного уравнения (18.6) или из (18.12) с учетом (18.9). Тогда получим
, то можно исходить непосредственно их укороченного уравнения (18.6) или из (18.12) с учетом (18.9). Тогда получим , (18.13)
, (18.13) . Обычно для определения мощности второй гармоники используют формулу, которую в приближении заданного поля основного излучения записывают с учетом (18.4) в следующем виде
. Обычно для определения мощности второй гармоники используют формулу, которую в приближении заданного поля основного излучения записывают с учетом (18.4) в следующем виде , (18.14)
, (18.14) – длина волны основного излучения;
– длина волны основного излучения;  ,
,  - длина образца,
- длина образца,  и
и 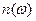 - показатели преломления волн частоты
- показатели преломления волн частоты 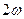 и
и 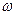 ,
,  .
. (19.1)
(19.1) ;
;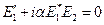 , (19.2)
, (19.2) , причем
, причем 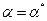 ;
;  ;
;  ;
;  .
. ,
,  . (19.3)
. (19.3) ;
; (19.4)
(19.4)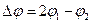 :
: . (19.5)
. (19.5) есть его решение (причем при
есть его решение (причем при  эта разность фаз устойчива). Тогда система (14.4) имеет первый интеграл
эта разность фаз устойчива). Тогда система (14.4) имеет первый интеграл . (19.6)
. (19.6) . (19.7)
. (19.7) . (19.8)
. (19.8) , (20.1)
, (20.1) , и которое имеет решение в виде двух слагаемых:
, и которое имеет решение в виде двух слагаемых: , (20.2)
, (20.2) . (20.3)
. (20.3)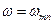 или
или  не дают существенного выигрыша в преобразовании основной волны в третью гармонику. Однако в отличие от генерации второй гармоники резонанс
не дают существенного выигрыша в преобразовании основной волны в третью гармонику. Однако в отличие от генерации второй гармоники резонанс  приводит к резкому увеличению
приводит к резкому увеличению  , как это видно из формулы (17.16). Эта особенность влечет за собой своеобразный эффект просветления: двухфотонное поглощение компенсируется преобразованием третьей гармоники в основную волну. Детально эти вопросы изложены в работе [17]. В последние годы эффект генерации третьей гармоники при двухфотонном резонансе нашел применение в создании источников когерентного излучения в ультрафиолетовом диапазоне [15].
, как это видно из формулы (17.16). Эта особенность влечет за собой своеобразный эффект просветления: двухфотонное поглощение компенсируется преобразованием третьей гармоники в основную волну. Детально эти вопросы изложены в работе [17]. В последние годы эффект генерации третьей гармоники при двухфотонном резонансе нашел применение в создании источников когерентного излучения в ультрафиолетовом диапазоне [15]. ) необыкновенной волны (плоскость поляризации лежит в главном сечении, то есть в плоскости, образованной волновым вектором и осью кристалла) путем изменения угла между волновым вектором основной волны и осью кристалла.
) необыкновенной волны (плоскость поляризации лежит в главном сечении, то есть в плоскости, образованной волновым вектором и осью кристалла) путем изменения угла между волновым вектором основной волны и осью кристалла. выполняется в направлении, перпендикулярном к оси кристалла (поверхности волновых векторов обыкновенной и необыкновенной волны в этом случае касаются). Это расширяет интервал углов для фазового согласования [14].
выполняется в направлении, перпендикулярном к оси кристалла (поверхности волновых векторов обыкновенной и необыкновенной волны в этом случае касаются). Это расширяет интервал углов для фазового согласования [14]. или
или  . В парах металлов это достигается путем добавлении буферного газа. Выбирая подходящий буферный газ и используя его плотность в качестве регулируемой переменной, можно выполнить пространственный синхронизм в следующей форме:
. В парах металлов это достигается путем добавлении буферного газа. Выбирая подходящий буферный газ и используя его плотность в качестве регулируемой переменной, можно выполнить пространственный синхронизм в следующей форме: .
.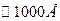 ), и появилась надежда создать источники когерентного излучения в мягком рентгеновском диапазоне (
), и появилась надежда создать источники когерентного излучения в мягком рентгеновском диапазоне ( ).
). и
и  фиксированы по амплитуде, тогда из уравнений Максвелла методом, рассмотренным в §18, для третьей волны частоты
фиксированы по амплитуде, тогда из уравнений Максвелла методом, рассмотренным в §18, для третьей волны частоты  получим
получим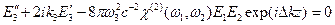 , (22.1)
, (22.1) . (22.2)
. (22.2) , (22.3)
, (22.3) (22.4)
(22.4) . В этом случае необходимо исходить из анализа укороченной системы уравнений (18.3).
. В этом случае необходимо исходить из анализа укороченной системы уравнений (18.3). генерируется путем сложения двух частот
генерируется путем сложения двух частот 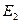 сводится к тривиальному:
сводится к тривиальному:  , а два других (дополнительно дифференцируя каждое и подставляя одно в другое) примут вид
, а два других (дополнительно дифференцируя каждое и подставляя одно в другое) примут вид
 (22.5)
(22.5) . (22.6)
. (22.6)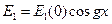 ; (22.7)
; (22.7) .
.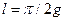 .
. поле сигнала и холостой волны определяется из уравнений
поле сигнала и холостой волны определяется из уравнений
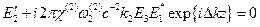 (22.8)
(22.8) . Дифференцируя еще раз каждое из уравнений и подставляя одно в другое, приходим к системе независимых уравнений второго порядка
. Дифференцируя еще раз каждое из уравнений и подставляя одно в другое, приходим к системе независимых уравнений второго порядка ;
; , (22.9)
, (22.9) . (22.10)
. (22.10) имеет вид
имеет вид , (22.11)
, (22.11) имеем
имеем  , то есть экспоненциальный рост мощности. Для параметрического усиления при взятых выше граничных условиях существуют выражения для сигнала
, то есть экспоненциальный рост мощности. Для параметрического усиления при взятых выше граничных условиях существуют выражения для сигнала . (22.12)
. (22.12) . (22.13)
. (22.13)
 (22.14)
(22.14) ) приводит к уменьшению эффективности параметрического усиления. Характеристическое уравнение для каждого из (22.9) имеет вид
) приводит к уменьшению эффективности параметрического усиления. Характеристическое уравнение для каждого из (22.9) имеет вид , (22.15)
, (22.15) . (22.16)
. (22.16)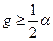 , (22.17)
, (22.17)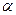 – коэффициент поглощения [7].
– коэффициент поглощения [7].
 ,
, ;
;  ;
;  - векторы и частоты фотонов и фонона, следует, что смещение частоты
- векторы и частоты фотонов и фонона, следует, что смещение частоты  составит величину:
составит величину: , (23.2)
, (23.2) - показатель преломления среды;
- показатель преломления среды; 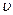 и
и  - фазовые скорости звука в среде и света в вакууме;
- фазовые скорости звука в среде и света в вакууме;  - угол между векторами
- угол между векторами  и
и  (угол рассеяния).
(угол рассеяния). , (23.3)
, (23.3) и
и  – плотность и скорость жидкости;
– плотность и скорость жидкости;  - давление;
- давление;  и
и  - сдвиговый и объемный коэффициенты вязкости;
- сдвиговый и объемный коэффициенты вязкости;  - внешняя сила, действующая на единицу объема жидкости (в переменном электрическом поле) [2]:
- внешняя сила, действующая на единицу объема жидкости (в переменном электрическом поле) [2]: (23.4)
(23.4)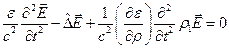 , (23.5)
, (23.5) есть отклонение от равновесной плотности. Полагая, что
есть отклонение от равновесной плотности. Полагая, что  , можно провести линеаризацию уравнения (23.3). Учитывая также уравнение непрерывности и связь между давлением и плотностью (
, можно провести линеаризацию уравнения (23.3). Учитывая также уравнение непрерывности и связь между давлением и плотностью (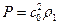 ,
,  - скорость звука), получим
- скорость звука), получим (23.6)
(23.6)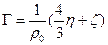 ;
;  . Чтобы учесть поглощение световой волны, введем в уравнение (23.5) дополнительное слагаемое с проводимостью, и представим уравнение в виде
. Чтобы учесть поглощение световой волны, введем в уравнение (23.5) дополнительное слагаемое с проводимостью, и представим уравнение в виде . (23.7)
. (23.7) (23.8)
(23.8) (23.9)
(23.9) и
и  постоянными. Тогда после подстановки (23.8) и (23.9) в (23.6) и (23.7) получим систему однородных алгебраических уравнений для нахождения
постоянными. Тогда после подстановки (23.8) и (23.9) в (23.6) и (23.7) получим систему однородных алгебраических уравнений для нахождения  , (23.10)
, (23.10) ;
;  , (23.11)
, (23.11) - показатель преломления среды. Если
- показатель преломления среды. Если  , то получаем известные законы дисперсии для акустических колебаний и электромагнитных волн:
, то получаем известные законы дисперсии для акустических колебаний и электромагнитных волн: ,
, 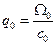 ;
; ,
,  . (23.12)
. (23.12) уравнение (23.10) представляет собой определение новых возбуждений в среде, которые невозможно разделить лишь на звуковую и электромагнитную ветви.
уравнение (23.10) представляет собой определение новых возбуждений в среде, которые невозможно разделить лишь на звуковую и электромагнитную ветви. . За положительное направление возьмем направление стоксовой компоненты и будем искать решение уравнений (23.6) и (23.7) в виде
. За положительное направление возьмем направление стоксовой компоненты и будем искать решение уравнений (23.6) и (23.7) в виде
 (23.13)
(23.13)
 (23.14)
(23.14) ,
, 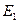 и
и  представляют собой функции координаты
представляют собой функции координаты 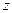 и времени
и времени  . Рассмотрим случай, когда они мало меняются на расстояниях порядка длин волн (звука и света) и за времена порядка периодов колебаний в волнах. Подставим в (23.13) в уравнения (23.6) и (23.7) и сохраним лишь первые производные по переменным. Получим систему уравнений
. Рассмотрим случай, когда они мало меняются на расстояниях порядка длин волн (звука и света) и за времена порядка периодов колебаний в волнах. Подставим в (23.13) в уравнения (23.6) и (23.7) и сохраним лишь первые производные по переменным. Получим систему уравнений
 (23.15)
(23.15) . Решение системы уравнений ищем в виде
. Решение системы уравнений ищем в виде
 (23.16)
(23.16) и
и  , условие разрешимости которой дает следующее дисперсионное уравнение:
, условие разрешимости которой дает следующее дисперсионное уравнение: , (23.17)
, (23.17)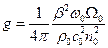 . Обычно коэффициент поглощения звука относительно превосходит коэффициент поглощения света. В стационарном режиме (
. Обычно коэффициент поглощения звука относительно превосходит коэффициент поглощения света. В стационарном режиме (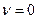 ) при условии, что
) при условии, что 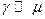 , уравнение (23.17) легко решается и дает два корня
, уравнение (23.17) легко решается и дает два корня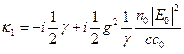 ,
, , (23.18)
, (23.18) ). Из (23.18) следует, что поглощение стоксовой компоненты ослабляется, и при условии
). Из (23.18) следует, что поглощение стоксовой компоненты ослабляется, и при условии (23.19)
(23.19)


