
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Колебание маятника при наличии тренияСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Поскольку сила трения при малых скоростях пропорциональна скорости, а скорость
Преобразуем (2.16) к виду
где При малых колебаниях уравнение (2.17) превращается в уравнение
Уравнение (2.18) описывает два вида колебаний: затухающие колебания при при
где при
Аналитического решение уравнения (2.17) не известно, поэтому его решают с помощью численных методов, предварительно сведя уравнение (2.17) к следующей системе дифференциальных уравнений
Наличие трения в колебательном движении приводит, в частности, к тому, что в зависимости от соотношения Входные параметры модели: Вынужденные колебания Если на маятник воздействует внешняя сила
где
Движение, описываемое уравнением (2.20), состоит из двух этапов. На первом оно складывается из двух колебательных движений: затухающих собственных колебаний с частотой
(2.21)
Исследование переходного процесса установления стационарных вынужденных колебаний, резонанса, биений, (рис. 2.5, 2.6, 2.7) возникающих при
Рис. 2.5. Установление стационарных вынужденных колебаний маятника при наличии трения
Рис. 2.6. Биения в системе с близкими частотами собственных колебаний и с вынуждающей силой
Рис. 2.7. Возрастание амплитуды колебаний при прохождения через резонанс Для численного решения уравнения (2.19), последнее первоначально сводится к системе уравнений
а затем приближенно решается одним из разностных методов. Входными параметрами модели являются Параметрические колебания Колебательные движения маятника, когда на него внешние силы непосредственно не действуют, но внутри системы происходят некоторые события, приводящие к зависимости от времени параметров, входящих в уравнение движения называются параметрическими. Простейшим примером является раскачивание качелей усилиями того человека, который стоит на качелях. Приседая и отталкиваясь можно сильно разогнать качели. Указанные приседания сводятся к периодическому изменению центра тяжести системы, или, что почти равносильно, длины нити подвеса. Поскольку длина нити подвеса определяет частоту колебаний, то математической моделью является уравнение
где
где
Одно из принципиальных явлений, связанное с этими колебаниями – появление так называемого параметрического резонанса при некоторых соотношениях частот
Рис. 2.8. Фазовая диаграмма с зонами параметрического резонанса Рассмотренные выше уравнения, особенно линейные, описывают ряд процессов в механике твердых тел, газов, в электродинамике и т.д. Например, уравнение
2.6. Моделирование явлений и процессов в приближении сплошной среды. Абстрактное понятие «сплошная среда» широчайшим образом используется в науке. Во многих ситуациях жидкости, газы, твердые тела, плазму можно рассматривать как «сплошные», отвлекаясь от их молекулярного и атомарного устройства. Например, при распространении волн в жидкости или газе реальная дискретность этих сред практически не сказывается на свойствах волн, если длина волны многобольше характерного межмолекулярного расстояния. При изучении процесса распространения тепла или диффузии чаще оперируют такими характеристиками как теплоемкость, теплопроводность, скорость диффузии, которые можно обсуждать и практически использовать в технике без выяснения их микроскопической природы. В приближении сплошной среды свойства объекта описываются математически с помощью непрерывных функций от координат и времени: Существующие задачи можно разделить на два класса: статические и динамические. В первом случае значения величин, характеризующих сплошную среду, не зависят от времени, и требуется найти их пространственное распределение. Примеры задач: как распределено в пространстве значение электрического поля, созданного неподвижным точечным зарядом? как распределены электрическое поле в конденсаторе? поле постоянного магнита? скорости в стационарно движущемся по трубе потоке жидкости? Еще сложнее решение динамических задач. Если электрическое поле создается движущимися зарядами, то определить, как оно меняется во времени в каждой точке пространства – очень непростая задача. Не менее трудно определить эволюцию скорости в разных местах в жидкости, если в некотором месте пульсирует давление; изменения значений температуры в разных точках некоторого тела, которое подогревают изнутри или извне от источников тепла, интенсивность которых изменяется со временем. Если поле создается одним точечным зарядом Если поле создано не одним, а несколькими зарядами, то напряженность и потенциал в каждой точке можно найти из принципа суперпозиции:
где Зная потенциал в каждой точке поля, т.е. функцию
В реальных конструкциях поле создается достаточно причудливо расположенными в пространстве заряженными телами самых разных форм: пластины, плоские и изогнутые; штыри; правильные и деформированные сфероиды и т.д. Важно иметь наглядную картину поля, изображенного некоторым условным образом. Существуют два классических способа для наглядного изображения поля: поверхностями (или линиями) равного потенциала и силовыми линиями поля.
Для любого электростатического поля множество точек, потенциал в которых одинаков,образует замкнутую поверхность – эквипотенциальную поверхность. Для одного точечного заряда это сфера; в общем случае эта поверхность может быть очень сложной. Линии равного потенциала являются сечениями поверхности равного потенциала той плоскостью, в которой строится изображение. Силовые линии – линии, касательные к которым в каждой точке задают направление вектора напряженности поля. Силовые линии никогда не пересекаются между собой. Они начинаются на положительных зарядах и либо заканчиваются на отрицательных, либо уходят «на бесконечность». По соглашению число силовых линий, исходящих из точечного заряда, пропорционально величине этого заряда; коэффициент пропорциональности выбирается таким, чтобы изображение было легко читаемым. Ниже описывается практический метод построения картины поверхностей равного потенциала для системы, состоящей из нескольких точечных зарядов произвольной величины и знака, любым способом расположенных в пространстве. Введем некоторую систему координат, начало которой удобнее расположить в «пустой» точке, т.e. ни на одном из зарядов. Пусть в этой системе координаты зарядов имеют значения Рассмотрим вначале построение линий равного потенциала (изолиний), образованных сечением поверхности равного потенциала некоторой плоскостью; пусть, для определенности, это будет плоскость Выберем по осям
Ограничимся прямоугольной областью в плоскости
Фиксируем некоторое значение потенциала
Если такая пара узлов найдена, то координату точки, в которой
Найдя в данной горизонтали все такие точки, переходим к следующей горизонтали, пока не пройдем их все. После этого следует аналогичный поиск нужных точек на вертикальных линиях сетки. Формулы, аналогичные (2.24), имеют вид:
После прохождения всех горизонтальных и вертикальных линий сетки находятся все те точки на этих линиях, в которых потенциал равен Если между двумя ближайшими узлами выполняется записанное выше неравенство – означает ли это, что между ними действительно лежит однаточка, в которой
Рис. 2.9. Приближенное нахождение точки, в которой
Рис. 2.10. Формальное нахождение точки, в которой Для получения изолиний следует брать достаточно малые program isoliniya; uses crt, graph; const n=100;{ k=5; l=9;} k=7; l=9; q:array[1..k] of real={(1,-2,2,-3,1)} (1,1,1,1,-1,-1,-1); x:array[1..k] of real={(0.3,0.2,0.7,0.5,0.5)}(0.2,0.8,0.2,0.8,0.2,0.5,0.8); y:array[1..k] of real={(0.75,0.5,0.2,0.9,0.5)}(0.2,0.8,0.8,0.2,0.5,0.5,0.5); p:array[1..l] of real={(-4,-3,-2,-1,0,1,2,3,4)} (-4,-3,-2,-1,0,1,2,3,4); var { x,y,q:array[1..k] of real;} { p:array[1..l] of real; } fi:array[0..n,0..n] of real; i,j,m,adapter,regim:integer; a,b,r,pp:real; begin clrscr; { for i:=1 to k do begin write('x[',i,']='); readln(x[i]); write('y[',i,']='); readln(y[i]); write('q[',i,']='); readln(q[i]); end; } for i:=0 to n do for j:=0 to n do for m:=1 to k do begin r:=sqrt(sqr((i/n)-x[m])+sqr((j/n)-y[m])); if r>=1e-6 then fi[i,j]:=fi[i,j]+(q[m]/r) else fi[i,j]:=1e+8; end; { for i:=1 to l do begin write('p[',i,']='); readln(p[i]); end; } adapter:=detect; initgraph(adapter,regim,'d:\lang\bp\bgi'); for i:=1 to k do begin a:=x[i]*getmaxx; b:=(1-y[i])*getmaxy; circle(round(a),round(b),4); floodfill(round(a),round(b),getcolor);
end; for m:=1 to l do begin pp:=p[m]; setcolor(m); for i:=0 to n do for j:=0 to n-1 do if (fi[i,j]-pp)*(fi[i,j+1]-pp)<0 then begin a:=(j+(pp-fi[i,j])/(fi[i,j+1]-fi[i,j]))/n; circle(round((i/n)*getmaxx), round((1-a)*getmaxy),1); end; for j:=0 to n do for i:=0 to n-1 do if (fi[i,j]-pp)*(fi[i+1,j]-pp)<0 then begin a:=(i+(pp-fi[i,j])/(fi[i+1,j]-fi[i,j]))/n; circle(round(a*getmaxx), round((1-(j/n))*getmaxy),1); end; end; repeat until keypressed; readln; closegraph; end. Для построения силовых линий поля выберем некоторую точку с координатами (
по правилу суперпозиции
где Проведем в точке (
В результате получаем координаты точки Построение картины силовых линий, дающих представление о поле – дело неформальное, требующее понимания физической сущности. Два семейства взаимно перпендикулярных линий – равного потенциала и силовых – дают наглядную и исчерпывающую характеристику силового поля [3]. Учитывая трудности визуализации трехмерных изображений, целесообразно на практике вначале ограничиться рассмотрением ситуаций, когда все заряды лежат в одной плоскости; тогда силовая линия, начинающаяся из любой точки данной плоскости, из этой плоскости не выйдет, и получится легко воспринимаемая картина. 2.7. Моделирование процесса теплопроводности. Если один из концов длинного стержня поместить в костер, то, если стержень сделан не из горючего или легко плавящегося материала, другой конец через некоторое время тоже нагреется; как быстро и насколько – зависит от материала, размеров стержня и других факторов. Процесс теплопроводности – один из процессов тепломассопереноса. Другими процессами такого рода являются – диффузия, процессы гидро- и аэродинамики (процессы движения жидкостей и газов). Рассмотрим линейный стержень, боковая поверхность которого не проводит тепла (теплоизолирована). Если в начальный момент времени стержень неравномерно нагрет, то в нем будет происходить перераспределение тепла; при отсутствии внутренних источников тепла его температура выровняется. Поскольку стержень линеен и однороден, то распределение температуры в пространстве характеризуется одной координатой Получим уравнение, описывающее процесс изменения температуры в стержне. Зафиксируем некоторую точку
Рис. 2.11. Участок линейного стержня Количества тепла, проходящего через поперечное сечение стержня в точке Вводя коэффициент пропорциональности
Значение Количество тепла, проходящего через сечение в точке
с условием, что производная Ограничиваясь первым порядком приращения
На основании последнего соотношения следует, что
Если через сечение
Пусть за то же время температура участка изменилась на
Представляя массу в виде
где Уравнение (2.26) – основное уравнение теплопроводности для однородного стержня. Уравнение выражает закон сохранения энергии в данный момент времени в данной точке. Далее приводится вывод уравнения теплопроводности в трехмерном случае. Рассмотрим некоторое тело
Рис. 2.12. Иллюстрация к выводу уравнения теплопроводности в трехмерном случае Закон сохранения энергии выполняется для любой части тела
Применяя к правой части теорему Остроградского – Гаусса, получаем
Поскольку это соотношение должно выполняться для любой части тела
где Уравнения (2.26), (2.27) описывают процесс изменения температуры тела во времени и пространстве. Для отслеживания данного процесса нужно знать распределение температуры в теле в начальный момент времени:
где
Дифференциальное уравнение (2.26) при начальном условии (2.28) и краевых условиях (2.29) имеет единственное решение. Рассмотрим методы численного интегрирования уравнений в частных производных на примере решения уравнения теплопроводности. Разобьем отрезок решения Аппроксимация первой производной в точке
Для крайних точек такая аппроксимация невозможна, поэтому простейший способ – ограничиться односторонними разностями:
Формулы (2.30) и (2.31) дают простейшие аппроксимации. Используя большое количество узлов, можно получить аппроксимации более высокого порядка, но часто бывает достаточно описанных выше. Аппроксимация вторых производных имеет вид
В качестве методов численного интегрирования используются те же методы, что и для решения обыкновенных дифференциальных уравнений: Эйлера, Рунге – Кутта. При интегрировании уравнений по времени двигаются по отдельным слоям, и в каждом слое определяют значение искомой функции на пространственной сетке. Если для интегрирования по времени используется метод Эйлера или другой одношаговый метод, то для работы со следующим временным слоем используются значения искомой функции из предыдущего слоя, для более сложных -из нескольких предыдущих слоев. Далее индексы, соответствующие временной сетке, пишутся надстрочно (вверху), а пространственной – подстрочно (внизу). Таким образом, для одномерного уравнения запись
где
Разностная схема (2.33) устойчива, если выполняется неравенство
Схема (2.33) с точки зрения быстродействия малоэффективна, но с точки зрения объема памяти вполне удовлетворительна, так как, получив значения
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 888; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.152.123 (0.016 с.) |

 , то уравнение свободных колебаний маятника с учетом трения имеет вид:
, то уравнение свободных колебаний маятника с учетом трения имеет вид: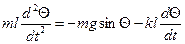 . (2.16)
. (2.16) , (2.17)
, (2.17) ,
, 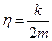 .
.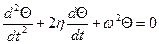 . (2.18)
. (2.18) и затухание колебаний при
и затухание колебаний при  . Уравнение (2.18) позволяет найти аналитическое решение:
. Уравнение (2.18) позволяет найти аналитическое решение: ,
, ,
,  – амплитуда,
– амплитуда,  – начальная фаза (
– начальная фаза ( и
и  );
); ,
, также выражаются через
также выражаются через 
 и
и  появляются разные режимы движения: затухающие колебания и затухание без колебаний. Одна из задач исследования – найти на фазовой плоскости
появляются разные режимы движения: затухающие колебания и затухание без колебаний. Одна из задач исследования – найти на фазовой плоскости  линию, разделяющую два режима, в зависимости от начального отклонения маятника [3, 4].
линию, разделяющую два режима, в зависимости от начального отклонения маятника [3, 4]. – начальная угловая скорость,
– начальная угловая скорость,  , то уравнение движение получается из (2.16) добавлением
, то уравнение движение получается из (2.16) добавлением 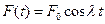 , где
, где  – частота вынужденной силы. В этом случае уравнение движение маятника имеет вид:
– частота вынужденной силы. В этом случае уравнение движение маятника имеет вид: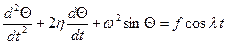 , (2.19)
, (2.19) . При малой амплитуде движения (2.19) примет вид
. При малой амплитуде движения (2.19) примет вид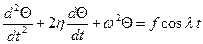 (2.20)
(2.20)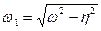 (при
(при  ) и вынужденных колебаний с частотой
) и вынужденных колебаний с частотой  , остаются лишь вынужденные периодические колебания, амплитуда которых зависит от соотношения частот
, остаются лишь вынужденные периодические колебания, амплитуда которых зависит от соотношения частот  и резко возрастает при
и резко возрастает при 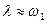 – явление резонанса. Аналитическое решение уравнения (2.20) имеет вид
– явление резонанса. Аналитическое решение уравнения (2.20) имеет вид .
. и
и  могут как проводится простым табулированием формулы (2.21) так и с помощью численного моделирования уравнения (2.20).
могут как проводится простым табулированием формулы (2.21) так и с помощью численного моделирования уравнения (2.20).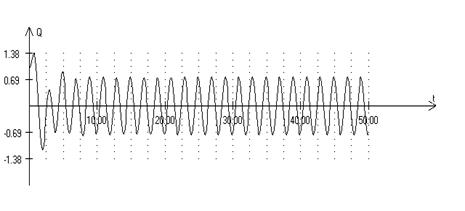



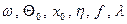 .
.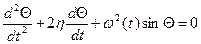 ,
, – заданная функция, определяющая закон изменения частоты. В случае гармонического изменения
– заданная функция, определяющая закон изменения частоты. В случае гармонического изменения 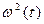 определяется по формуле
определяется по формуле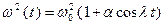 , (2.22)
, (2.22)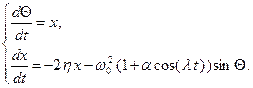
 , а именно
, а именно  ,
, 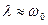 ,
,  ,
,  ,
,  и при определенных значениях величины
и при определенных значениях величины  в системе возникают нарастающие колебания. На рис. 2.8 схематически изображена фазовая диаграмма системы в переменных
в системе возникают нарастающие колебания. На рис. 2.8 схематически изображена фазовая диаграмма системы в переменных  и
и 
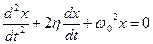 описывает следующие системы: математический маятник; пружинный маятник; «физический» маятник – тело, свободно вращающееся около горизонтальной оси; крутильный маятник наручных часов – симметричное тело, совершающее колебания около вертикальной оси под действием спиральной пружины; ток в колебательном контуре; акустический резонатор Гельмгольца, в котором происходит колебания воздуха в колбе с широким горлышком; колебания магнитной стрелки компаса.
описывает следующие системы: математический маятник; пружинный маятник; «физический» маятник – тело, свободно вращающееся около горизонтальной оси; крутильный маятник наручных часов – симметричное тело, совершающее колебания около вертикальной оси под действием спиральной пружины; ток в колебательном контуре; акустический резонатор Гельмгольца, в котором происходит колебания воздуха в колбе с широким горлышком; колебания магнитной стрелки компаса.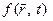 . За каждым «свойством» закрепляется такая функция, и их взаимосвязанный вид дает полное описание среды.
. За каждым «свойством» закрепляется такая функция, и их взаимосвязанный вид дает полное описание среды. ,то величина напряженности поля зависит от расстояния
,то величина напряженности поля зависит от расстояния 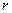 от
от  . Поле существует независимо от пробного заряда
. Поле существует независимо от пробного заряда  и может рассматриваться как сплошная среда. Существуют две взаимосвязанные характеристики электрического поля: напряженность
и может рассматриваться как сплошная среда. Существуют две взаимосвязанные характеристики электрического поля: напряженность  и потенциал
и потенциал 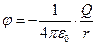 .
. ,
,  ,
, и
и  создаются в этой точке
создаются в этой точке  -м зарядом.
-м зарядом. , можно найти напряженность в каждой точке чисто математическим путем на основании того, что проекция вектора напряженности на любое направление есть скорость изменения потенциала в этом направлении:
, можно найти напряженность в каждой точке чисто математическим путем на основании того, что проекция вектора напряженности на любое направление есть скорость изменения потенциала в этом направлении: ,
,  ,
, 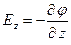 . (2.23)
. (2.23)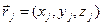 ,
,  , где
, где  –число зарядов.
–число зарядов. . Воспользуемся методом сеток.
. Воспользуемся методом сеток.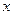 ,
,  некоторые шаги
некоторые шаги  ,
,  и покроем плоскость сеткой, образованной прямыми, параллельными осям
и покроем плоскость сеткой, образованной прямыми, параллельными осям  , следующий по оси
, следующий по оси 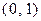 , влево –
, влево –  ; по оси
; по оси  , вниз
, вниз  и т.д. Значения потенциала, создаваемого системой зарядов
и т.д. Значения потенциала, создаваемого системой зарядов  в узле
в узле  , согласно принципу суперпозиции, имеет вид (здесь и ниже
, согласно принципу суперпозиции, имеет вид (здесь и ниже  – столбца сетки):
– столбца сетки): .
.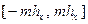 по оси
по оси  по оси
по оси  узлов. Вычислим значения потенциала в каждом из них по указанным формулам. В результате получим матрицу значений потенциала.
узлов. Вычислим значения потенциала в каждом из них по указанным формулам. В результате получим матрицу значений потенциала. и построим изолинию, соответствующую этому значению. Для этого проходим, к примеру, по
и построим изолинию, соответствующую этому значению. Для этого проходим, к примеру, по  .
. , найдем приближенно с помощью линейной интерполяции:
, найдем приближенно с помощью линейной интерполяции: ,
,  . (2.24)
. (2.24)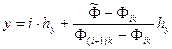 ,
,  . (2.25)
. (2.25) ? Да, если потенциал между этими узлами меняется монотонно. Если же узлы столь редки (т.е.
? Да, если потенциал между этими узлами меняется монотонно. Если же узлы столь редки (т.е. 
 , с помощью линейной интерполяции
, с помощью линейной интерполяции
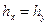 ),а затем с вдвое меньшими значениями; если картины близки, то построение на этом завершается. Даже если все заряды лежат в одной плоскости, поле существует, конечно, и вне этой плоскости. Один из способов наглядного построения изображения поля – найти изолинии, соответствующие некоторому фиксированному набору значений
),а затем с вдвое меньшими значениями; если картины близки, то построение на этом завершается. Даже если все заряды лежат в одной плоскости, поле существует, конечно, и вне этой плоскости. Один из способов наглядного построения изображения поля – найти изолинии, соответствующие некоторому фиксированному набору значений  ,
,  ,
,  ) и найдем в ней напряженность поля
) и найдем в ней напряженность поля
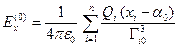 ,
, 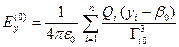 ,
,  ,
, .
. , и возьмем вдоль нее небольшой отрезок длины
, и возьмем вдоль нее небольшой отрезок длины  , начинающийся в
, начинающийся в  ,
,  ,
, 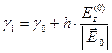 .
. лежащей на касательной к силовой линии (вместо точки
лежащей на касательной к силовой линии (вместо точки 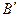 вблизи силовой линии и т.д. Ломанная
вблизи силовой линии и т.д. Ломанная  приблизительно передает силовую линию. Построение целесообразно начать вблизи какого-нибудь положительного заряда (если он есть) и закончить тогда, когда силовая линия подойдет вплотную к отрицательному заряду или уйдет «на бесконечность».
приблизительно передает силовую линию. Построение целесообразно начать вблизи какого-нибудь положительного заряда (если он есть) и закончить тогда, когда силовая линия подойдет вплотную к отрицательному заряду или уйдет «на бесконечность». ) зависит от времени
) зависит от времени  –
–  .
.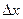 . Искомое уравнение есть уравнение теплового баланса: изменение количества тепла в выбранном участке стержня за счет притока и (или) оттока его через сечения приведет к нагреванию или охлаждению этого участка в соответствии с его теплоемкостью.
. Искомое уравнение есть уравнение теплового баланса: изменение количества тепла в выбранном участке стержня за счет притока и (или) оттока его через сечения приведет к нагреванию или охлаждению этого участка в соответствии с его теплоемкостью.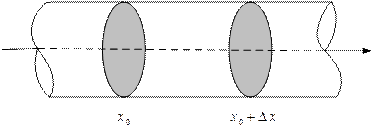
 , пропорционально площади поперечного сечения
, пропорционально площади поперечного сечения  , градиенту температуры
, градиенту температуры 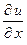 и промежутку времени
и промежутку времени 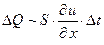 . Пропорциональность градиенту температуры следует из экспериментального факта: поток тепла
. Пропорциональность градиенту температуры следует из экспериментального факта: поток тепла  через некоторый участок стержня длиной
через некоторый участок стержня длиной  ) на его концах и чем меньше расстояние
) на его концах и чем меньше расстояние  при
при  .
. .
. .
. , определяется формулой:
, определяется формулой: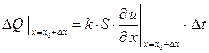
 .
. .
. и
и  прошло разное количества тепла, то та его часть, которая пошла на нагревание (или, в зависимости от знака, на охлаждение) этого участка стержня определяется формулой
прошло разное количества тепла, то та его часть, которая пошла на нагревание (или, в зависимости от знака, на охлаждение) этого участка стержня определяется формулой .
. . Тогда величина
. Тогда величина  , где
, где  – масса,
– масса,  – удельная теплоемкость. Приравнивая два выражения для
– удельная теплоемкость. Приравнивая два выражения для 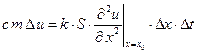 .
.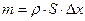 , поделив обе части уравнения на
, поделив обе части уравнения на  , получим
, получим , или
, или  , (2.26)
, (2.26) – коэффициент температуропроводности.
– коэффициент температуропроводности. , ограниченное поверхностью
, ограниченное поверхностью  (рис. 2.12).
(рис. 2.12).
 определяется как
определяется как  , где
, где  – объемная плотность энергии. Поток энергии через границу тела
– объемная плотность энергии. Поток энергии через границу тела 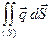 ,
,  – поток энергии. Закон сохранения энергии примет вид
– поток энергии. Закон сохранения энергии примет вид .
. .
. и в любой момент времени
и в любой момент времени  , (2.27)
, (2.27)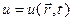 – температура в точке
– температура в точке 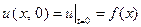 , (2.28)
, (2.28) – заданная функция. Кроме того, в местах, где возможен теплообмен с окружающей средой, надо знать условия этого обмена. Для стержня с теплоизолированной боковой поверхностью такими местами являются концы. Если один конец имеет координату
– заданная функция. Кроме того, в местах, где возможен теплообмен с окружающей средой, надо знать условия этого обмена. Для стержня с теплоизолированной боковой поверхностью такими местами являются концы. Если один конец имеет координату 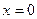 , а другой –
, а другой – 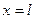 , то простейший вариант краевых условий – постоянная температура на каждом конце стержня:
, то простейший вариант краевых условий – постоянная температура на каждом конце стержня: ,
, 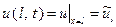 . (2.29)
. (2.29) на
на  равных частей с узлами в точках
равных частей с узлами в точках  ,…,
,…, 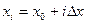 ,…,
,…,  . Искомую функцию
. Искомую функцию 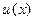 будем аппроксимировать ее значениями в узлах сетки.
будем аппроксимировать ее значениями в узлах сетки. имеет вид
имеет вид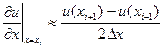 . (2.30)
. (2.30)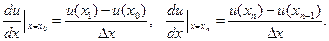 (2.31)
(2.31) ,
, (2.32)
(2.32) .
. означает значение функции
означает значение функции  в
в 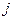 -м временном слое и в
-м временном слое и в  для внутренних узлов пространственной сетки на основе метода Эйлера находится из равенства
для внутренних узлов пространственной сетки на основе метода Эйлера находится из равенства , (2.33)
, (2.33) -шаг по координате,
-шаг по координате, 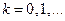 ,
, 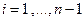 ,
, функция
функция  предполагается заданной и определяет значение температуры при
предполагается заданной и определяет значение температуры при 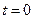 . Что касается значений
. Что касается значений  и
и  (на концах стержня), то они зависят от типа краевого условия; для случая, когда концы стержня поддерживаютсяпри постоянной температуре
(на концах стержня), то они зависят от типа краевого условия; для случая, когда концы стержня поддерживаютсяпри постоянной температуре ,
,  , где
, где 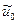 ,
,  - заданные числа.
- заданные числа.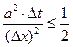 .
. на нек
на нек 


