
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы компьютерного моделированияСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Элементы компьютерного моделирования
Рекомендовано редакционно-издательским советом ГОУ ВПО «Таганрогский государственный педагогический институт» в качестве учебного пособия для студентов высших учебных заведений, обучающихся по специализации «Математика и информатика»
В авторской редакции
Таганрог Издательский центр Таганрогского государственного педагогического института УДК 517.91: 518.1 ББК 74.580.212+74.202.12 Р 93
Печатается по решению редакционно-издательского совета ГОУ ВПО «Таганрогский государственный педагогический институт»
Рецензенты: д-р техн. наук, проф. Я.Е. Ромм, д-р техн. наук, проф. В.И. Финаев
Буланов С.Г. Элементы компьютерного моделирования: –: Учеб. пособие / В авторской редакции. Таганрог: Изд-во Таганрог. гос. пед. ин-та, 2011. – 154 c.
Рассматривается схема компьютерного моделирования реальных процессов и явлений из различных областей науки. Конструируются математические модели преимущественно в виде систем дифференциальных уравнений, описывающие существенные характеристики изучаемого объекта. Представлены коды программ на языках Pascal и Delphi, динамически иллюстрирующие протекающие процессы, графически отображающие интересующиеся зависимости и находящие числовые значения параметров моделей. Для студентов вузов обучающихся по специальности математика и информатика, может быть полезно для преподавателей и лиц, занимающихся проблемами компьютерного моделирования.
УДК 517.91: 518.1 ББК 74.580.212+74.202.12
Содержание Введение ………………………………...………...………………... 4 Глава 1. Основные понятия о моделировании систем ……..……. 7 1.1. Моделирование как метод научного познания....………… 7 1.2. Классификация видов моделирования систем …………..... 9 Глава 2. Моделирование физических процессов ………...…...... 15 2.1. Свободное падение тела с учетом сопротивления среды.. 15 2.2. Движение тела с переменной массой: взлет ракеты …….. 20 2.3. Движение тела, брошенного под углом к горизонту ….… 24 2.4. Движение небесных тел. Законы Кеплера. Движение заряженных частиц ……………………………………………….…… 32
2.5. Колебания математического маятника ……………...…… 36 2.6. Моделирование явлений и процессов в приближении сплошной среды ………………………………………………...... 42 2.7. Моделирование процесса теплопроводности ……........…. 48 Глава 3. Моделирование в экологии …………………...….……. 56 3.1. Моделирование внутривидовой конкуренции ……..……. 56 3.2. Логистическая модель межвидовой конкуренции ………. 66 3.3. Динамика численности популяций хищника и жертвы.... 71 Глава 4. Математические модели в экономике …………….…... 76 4.1. Классификация экономико-математических методов и моделей ………………………………………………………………. 76 4.2. Балансовый метод. Схема межпродуктового баланса …... 78 4.3. Коэффициенты прямых и полных материальных затрат.. 84 4.4. Межотраслевые балансовые модели в анализе экономических показателей …………………………………………………. 86 4.5. Динамическая межотраслевая балансовая модель ………. 90 Глава 5. Математические модели в медицине и биологии ……. 97 5.1. Математическая модель лазер-индуцированного тромбообразования в микрососудах живых организмов …………………. 97 5.2. Исследование модели лазер-индуцированного тромбообразования ………………………………………..………………….. 101 5.3. Модель ростовых пульсаций в биологии …………..…… 107 5.4. Математические модели в иммунологии ………….……. 114 Библиографический список ……………………………….……. 127 Приложение 1 …………………………………………………… 128 Приложение 2 ………………………………………………..….. 130 Приложение 3 ……………………………………………..…….. 136 Введение
Компьютерное моделирование является мощным инструментом современной науки. В сочетании с классическими методами исследования компьютерное моделирование позволяет за короткое время получать надежные результаты. В основе компьютерного моделирования лежат математические модели, отражающие фундаментальные законы природы. Такими моделями являются, в основном, модели физических явлений. Если фундаментальные законы, которым подчиняется явление, известны мало, то конструируются имитационные модели, воспроизводящие элементарные явления процесса с сохранением их логической структуры и последовательности протекания во времени, что позволяет по исходным данным получить сведения о состояниях процесса в определенные моменты времени и дают возможность оценить характеристики системы.
Одним из наиболее трудных этапов моделирования реальных процессов является построение вербальной модели явления и перевод этой модели, создаваемой на основе представлений и законов какой-либо конкретной области знания, на математический язык. Именно этот этап моделирования играет важнейшую роль, определяя в принципиальном плане успех или неудачу всего исследования. Научить строить математические модели несложных процессов и явлений с дальнейшим их компьютерным и программным исследованием является главной задачей данного учебного пособия. Пособие состоит из введения, пяти глав и приложения, включающего примерные задания для практического решения, тестовые задания, темы курсовых и выпускных квалификационных работ. В первой главе приводятся основные определения, цели и схема компьютерного моделирования, описываются разновидности моделирования систем. Во второй и последующих главах строятся математические модели, отражающие процессы из различных областей современной науки. Конкретно вторая глава посвящена моделированию физических процессов. В ней рассмотрены такие классические задачи как движение тела в поле силы тяжести, движение тела, брошенного под углом к горизонту, движение тела с переменной массой, колебательные движения и др. Простейшие варианты этих моделей допускают точное аналитическое решение. Качественное исследование более сложных вариантов моделей, не допускающих точного аналитического решения, требует привлечения методов качественной теории дифференциальных уравнений. Каждая задача начинается с описания изучаемого процесса. Далее проводится его математическое описание вплоть до получения системы дифференциальных уравнений, моделирующей изучаемый процесс. Для некоторых задач приводятся программные модели, позволяющие визуализировать на экране компьютера протекающий процесс, находить приближенные значения неизвестных величин, графически отображать получаемые зависимости. В третьей главе рассматриваются задачи классической экологии. В первом разделе представлены модели внутривидовой конкуренции с непрерывным и дискретным периодом размножения. Описаны и графически проиллюстрированы возможные исходы развития популяций в зависимости от входных параметров моделей, подтверждающиеся результатами работы программ. Во втором разделе приводится логистическая модель внутривидовой конкуренции для двух популяций и схемы анализа исхода процесса на основе компьютерного моделирования системы дифференциальных уравнений, описывающих модель, и с помощью специальных диаграмм, на которых отображаются все возможные сочетания численности обоих видов. Правильное использование предложенных схем позволяет ответить на основной вопрос при исследовании межвидовой конкуренции, – при каких условиях увеличивается или уменьшается численность каждого вида. Третий раздел содержит решение классической задачи «хищник-жертва». Четвертая глава посвящена анализу статических и динамических балансовых моделей, которые применяются при экономико-математическом моделировании экономических систем и процессов. В первом разделе представлена классификация экономико-математических методов и моделей. Во втором и третьем разделах описан балансовый метод и схема межпродуктового баланса. Приводится экономико-математическая модель межотраслевого баланса – модель Леонтьева, на основе которой можно найти величины валовой и конечной продукции отраслей народного хозяйства.
В четвертом разделе приводится схема применение балансового метода в различных сферах. Представлена схема использования межотраслевого балансового метода для анализа таких экономических показателей, как труд, фонды и цены. Пятый раздел посвящен динамическим моделям, которые отражают не состояние, а процесс развития экономики, устанавливая взаимосвязь между предыдущим и последующим этапами развития. Пятая глава посвящена изучению математических моделей биологических систем. Первые два раздела содержат построение и исследование модели лазер-индуцированного тромбообразования в микрососудах живых организмов. Поведение и свойства таких систем определяются в равной мере физическими и биологическими факторами, поэтому их рассмотрение позволяет продемонстрировать применение общих принципов математического моделирования к объектам достаточно сложной природы. Третий раздел содержит изложение математической теории ростовых пульсаций в биологических объектах, которая наглядно демонстрирует эффективность учета физических факторов и концепций в процессе формирования определенных свойств биологических систем. Последний раздел этой главы посвящен построению и анализу математической модели иммунного ответа живого организма на вирусную инфекцию. Сложность изучаемой системы приводит к тому, что даже при наличии достаточно широкого спектра экспериментальных данных построение модели проводится в рамках интуитивного подхода на основе правдоподобных предположений. Качественный анализ модели позволяет оценить ее адекватность изучаемому явлению и обсудить возможность использования теоретических предсказаний в клинической практике.
Глава 1. Основные понятия о моделировании систем
1.1. Моделирование как метод научного познания. В настоящее время методы моделирования используются во многих областях человеческой деятельности – в механике, физике, экономике, экологии, теории автоматического регулирования, при управлении технологическими процессами, в задачах космической, аэро- и гидро- навигации, а также в ряде других областей науки и техники.
Особенно существенное применение эти методы нашли в сфере управления различными системами, где основными являются процессы принятия решений на основе получаемой информации. Введем следующие определения. Гипотеза – определенное предсказание, основывающееся на небольшом количестве опытных данных, наблюдений, догадок. Аналогия – суждение о каком либо частном сходстве двух объектов. Гипотезы и аналогии, отражающие реальный, объективно существующий мир, должны обладать наглядностью и сводиться к удобным для исследования логическим схемам. Моделью называются логические схемы, упрощающие рассуждения и логические построения и позволяющие проводить эксперименты, уточняющие природу явлений. Другими словами, модель – это объект заместитель объекта оригинала, обеспечивающий изучение некоторых свойств оригинала. Моделированием называется замещение одного объекта другим с целью получения информации о важнейших свойствах объекта оригинала с помощью объекта модели. Если результаты моделирования подтверждаются и могут служить основой для прогнозирования процессов, протекающих в исследуемых объектах, то говорят, что модель адекватна объекту. При этом адекватность модели зависит от цели моделирования и принятых критериев. Основные цели моделирования: 1) понять, как устроен конкретный объект, какова его структура, основные свойства, законы развития и взаимодействия с окружающим миром (понимание); 2) научиться управлять объектом (или процессом) и определить наилучшие способы управления при заданных целях и критериях (управление); 3) прогнозировать прямые и косвенные последствия реализации заданных способов и форм воздействия на объект (прогнозирование). Схема процесса компьютерного математического моделирования имеет вид:
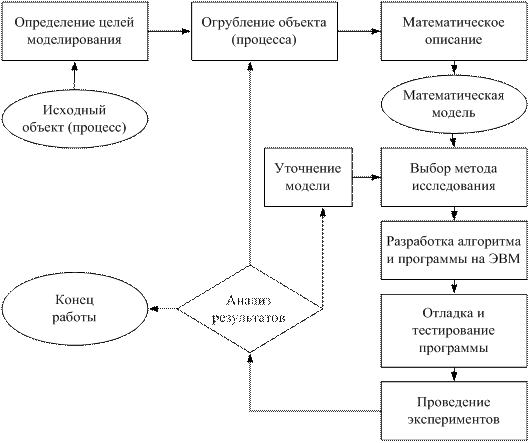
Рис. 1.1. Схема компьютерного моделирования Первый этап – определение целей моделирования, о которых было сказано выше. Вторым этапом является разделение входных параметров по степени важности влияния их изменений на выходные. Следующий этап – поиск математического описания. На этом этапе необходимо перейти от абстрактной формулировки модели к математической – в виде уравнения, системы уравнений, системы неравенств, дифференциального уравнения или систем дифференциальных уравнений. Когда математическая модель сформулирована, выбирается метод ее исследования. Обычно, для решения одной и той же задачи существует несколько конкретных методов, различающихся эффективностью, устойчивостью. Разработка алгоритма и составление программы для ЭВМ – это трудно формализуемый процесс. В настоящее время при компьютерном математическом моделировании наиболее распространенными являются приемы процедурно-ориентированного (структурного) программирования. После составления программы решается с ее помощью простейшая тестовая задача (желательно, с заранее известным ответом) с целью устранения грубых ошибок. В общем случае тестирование может продолжаться долго и закончиться тогда, когда пользователь по своим профессиональным признакам сочтет программу верной.
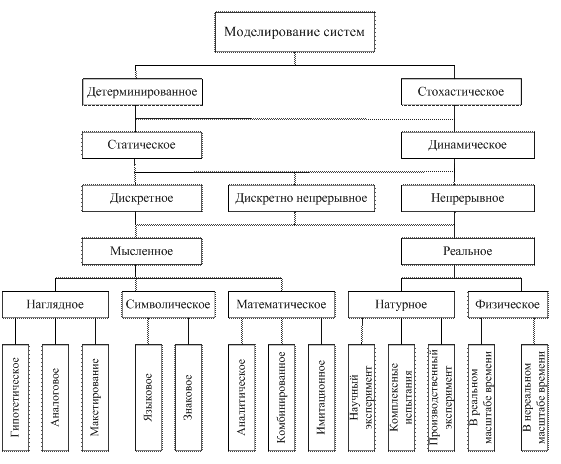
Затем следует численный эксперимент, и выясняется, соответствует ли модель реальному объекту (процессу). Модель адекватна реальному процессу, если некоторые характеристики процесса, полученные на ЭВМ, совпадают с экспериментальными, с заданной степенью точности. В случае несоответствия модели реальному процессу необходимо возвратиться к одному из предыдущих этапов. 1.2. Классификация видов моделирования систем. В зависимости от характера изучаемых процессов все виды моделирования могут быть разделены на детерминированные и стохастические, статические и динамические, дискретные, непрерывные и дискретно-непрерывные (рис. 1.2). Детерминированное моделированиеотображает процессы, в которых предполагается отсутствие всяких случайных воздействий. Стохастические моделированиеотображает вероятностные процессы и события. В этом случае анализируется ряд реализаций случайного процесса и оцениваются средние характеристики, т.е. набор однородных реализаций. Статическое моделированиеслужит для описания поведения объекта, в какой либо момент времени, динамическое моделированиеотражает поведение объекта во времени. Дискретное моделированиеслужит для описания процессов, которые предполагаются дискретными, соответственно непрерывное моделирование отражает непрерывные процессы в системах, а дискретно непрерывное моделированиеиспользуется для случаев, когда хотят выделить наличие как дискретных, так и непрерывных процессов [1, 2]. В зависимости от формы представления объекта можно выделить мысленное и реальное моделирование.
Рис. 1.2. Виды моделирования Мысленное моделирование часто является единственным способом моделирования объектов, которые либо практически не реализуемы в заданном интервале времени, либо существуют вне условий, возможных для их физического создания. Например, на базе мысленного моделирования могут быть проанализированы многие ситуации микромира, которые не поддаются физическому эксперименту. Мысленное моделирование может быть реализовано в виде наглядного, символического и математического. При наглядном моделировании на базе представлений человека о реальных объектах создаются различные наглядные модели, отображающие явления и процессы, протекающие в объекте. В основу гипотетического моделирования исследователем закладывается некоторая гипотеза о закономерностях протекания процесса в реальном объекте, которая отражает уровень знаний исследователя об объекте и базируется на причинно-следственных связях между входом и выходом изучаемого объекта. Гипотетическое моделирование используется, когда знаний об объекте недостаточно для построения формальных моделей. Аналоговое моделирование основывается на применении аналогий различных уровней. Наивысшим уровнем является полная аналогия, имеющая место только для достаточно простых объектов. С усложнением объекта используют аналогии последующих уровней, когда аналоговая модель отображает несколько либо только одну сторону функционирования объекта. Существенное место при мысленном наглядном моделировании занимает макетирование.Мысленный макет может применяться в случаях, когда протекающие в реальном объекте процессы не поддаются физическому моделированию, либо может предшествовать проведению других видов моделирования [1]. В основе языкового моделирования лежит тезариус – словарь, который очищен от неоднозначности, т.е. в нем каждому слову может соответствовать лишь единственное понятие. Тезариус образуется из набора входящих понятий, причем этот набор должен быть фиксированным. Символическое моделирование представляет собой искусственный процесс создания логического объекта, который замещает реальный и выражает основные свойства его отношений с помощью определенной системы знаков или символов. Для исследования характеристик процесса функционирования любой системы математическими методами, включая и машинные, должна быть проведена формализация этого процесса, т. е. построена математическая модель. Под математическим моделированием понимается процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью, и исследование этой модели, позволяющее получать существенные характеристики рассматриваемого реального объекта. Вид математической модели зависит как от природы реального объекта, так и от задач исследования объекта и требуемой достоверности и точности решения этой задачи. Для аналитического моделирования характерно то, что процессы функционирования элементов системы записываются в виде функциональных соотношений (алгебраических, дифференциальных, конечно-разностных) или логических условий. Аналитическая модель может быть исследована следующими методами: а) аналитическим, когда стремятся получить в общем виде явные зависимости для искомых характеристик; б) численным, когда, не умея решать уравнения в общем виде, стремятся получить числовые результаты при конкретных начальных данных; в) качественным, когда, не имея решения в явном виде, можно найти некоторые свойства решения (например, оценить устойчивость решения). При имитационном моделировании реализующий модель алгоритм воспроизводит процесс функционирования системы во времени, причем имитируются элементарные явления, составляющие процесс, с сохранением их логической структуры и последовательности протекания во времени, что позволяет по исходным данным получить сведения о состояниях процесса в определенные моменты времени, дающие возможность оценить характеристики системы. Основным преимуществом имитационного моделирования по сравнению с аналитическим является возможность решения более сложных задач. Имитационные модели позволяют достаточно просто учитывать такие факторы, как наличие дискретных и непрерывных элементов, нелинейные характеристики элементов системы, многочисленные случайные воздействия, которые часто создают трудности при аналитических исследованиях. Комбинированное моделирование позволяет объединить достоинства аналитического и имитационного моделирования при анализе и синтезе систем. При построении комбинированных моделей проводится предварительная декомпозиция процесса функционирования объекта на составляющие подпроцессы, и для тех из них, где это возможно, используются аналитические модели, а для остальных подпроцессов строятся имитационные модели. При реальном моделировании используется возможность исследования различных характеристик либо на реальном объекте целиком, либо на его части. Такие исследования могут проводиться как на объектах, работающих в нормальных режимах, так и при организации специальных режимов для оценки интересующих исследователя характеристик. Реальное моделирование является наиболее адекватным, но при этом его возможности с учетом особенностей реальных объектов ограничены. Натурным моделированием называют проведение исследования на реальном объекте с последующей обработкой результатов эксперимента на основе теории подобия. При функционировании объекта в соответствии с поставленной целью удается выявить закономерности протекания реального процесса. Такие разновидности натурного эксперимента, как производственный эксперимент и комплексные испытания,обладают высокой степенью достоверности. С развитием техники и проникновением в глубь процессов, протекающих в реальных системах, возрастает техническая оснащенность научного эксперимента. Он характеризуется широким использованием средств автоматизации, применением весьма разнообразных средств обработки информации, возможностью вмешательства человека в процесс проведения эксперимента. В соответствии с этим появилось новое научное направление – автоматизация научных экспериментов. Другим видом реального моделирования является физическое,отличающееся от натурного тем, что исследование проводится на установках, которые сохраняют природу явлений и обладают физическим подобием. В процессе физического моделирования задаются некоторые характеристики внешней среды и исследуется поведение либо реального объекта, либо его модели при заданных или создаваемых искусственно воздействиях внешней среды. Физическое моделирование может протекать в реальном и нереальном (псевдореальном) масштабах времени,а также может рассматриваться без учета времени. В последнем случае изучению подлежат так называемые «замороженные» процессы, которые фиксируются в некоторый момент времени. Наибольшие сложность и интерес с точки зрения верности получаемых результатов представляет физическое моделирование в реальном масштабе времени. С точки зрения математического описания объекта и в зависимости от его характера модели можно разделить на модели аналоговые (непрерывные), цифровые (дискретные) и аналого-цифровые (комбинированные). Под аналоговой моделью понимается подобная модель, которая описывается уравнениями, связывающими непрерывные величины. Под цифровой понимают модель, которая описывается уравнениями, связывающими дискретные величины, представленные в цифровом виде. Под аналого-цифровой понимается модель, которая может быть описана уравнениями, связывающими непрерывные и дискретные величины. Особое место в моделировании занимает кибернетическое моделирование, в котором отсутствует непосредственное подобие физических процессов, происходящих в моделях. В этом случае стремятся отобразить лишь некоторую функцию и рассматривают реальный объект как «черный ящик», имеющий ряд входов и выходов, и моделируются некоторые связи между выходами и входами. Чаще всего при использовании кибернетических моделей проводят анализ поведенческой стороны объекта при различных воздействиях внешней среды. В основе кибернетических моделей лежит отражение некоторых информационных процессов управления, что позволяет оценить поведение реального объекта.
Вопросы для самоконтроля
1. Что такое модель? Приведите примеры моделей, отражающие реальные физические процессы? 2. Что называется моделированием? Математическим моделированием? Компьютерным моделированием? 3. В чем отличие компьютерного моделирования от математического моделирования? 4. Что такое гипотеза? В чем отличие гипотезы от аналогии? 5. Какие основные цели моделирования? 6. Что вы понимаете под математическим описанием изучаемого объекта, процесса? 7. Как определить метод исследования математической модели? 8. Как на основе результатов численного эксперимента определить, адекватна ли модель реальному процессу? 9. Что вы понимаете под уточнением модели? 10. Какое моделирование называется детерминированным? Чем оно отличается от стохастического? 11. Что вы понимаете под дискретным моделированием? Приведите примеры дискретных моделей? 12. Какое моделирование называется мысленным? 13. Какое моделирование называется математическим? 14. Какое моделирование называется имитационным? В чем преимущество имитационного моделирования по сравнению с аналитическим? 15. Что такое натурное моделирование? Какие разновидности натурного эксперимента вы знаете? Вынужденные колебания Если на маятник воздействует внешняя сила
где
Движение, описываемое уравнением (2.20), состоит из двух этапов. На первом оно складывается из двух колебательных движений: затухающих собственных колебаний с частотой
(2.21)
Исследование переходного процесса установления стационарных вынужденных колебаний, резонанса, биений, (рис. 2.5, 2.6, 2.7) возникающих при
Рис. 2.5. Установление стационарных вынужденных колебаний маятника при наличии трения
Рис. 2.6. Биения в системе с близкими частотами собственных колебаний и с вынуждающей силой
Рис. 2.7. Возрастание амплитуды колебаний при прохождения через резонанс Для численного решения уравнения (2.19), последнее первоначально сводится к системе уравнений
а затем приближенно решается одним из разностных методов. Входными параметрами модели являются Параметрические колебания Колебательные движения маятника, когда на него внешние силы непосредственно не действуют, но внутри системы происходят некоторые события, приводящие к зависимости от времени параметров, входящих в уравнение движения называются параметрическими. Простейшим примером является раскачивание качелей усилиями того человека, который стоит на качелях. Приседая и отталкиваясь можно сильно разогнать качели. Указанные приседания сводятся к периодическому изменению центра тяжести системы, или, что почти равносильно, длины нити подвеса. Поскольку длина нити подвеса определяет частоту колебаний, то математической моделью является уравнение
где
где
Одно из принципиальных явлений, связанное с этими колебаниями – появление так называемого параметрического резонанса при некоторых соотношениях частот
Рис. 2.8. Фазовая диаграмма с зонами параметрического резонанса Рассмотренные выше уравнения, особенно линейные, описывают ряд процессов в механике твердых тел, газов, в электродинамике и т.д. Например, уравнение 2.6. Моделирование явлений и процессов в приближении сплошной среды. Абстрактное понятие «сплошная среда» широчайшим образом используется в науке. Во многих ситуациях жидкости, газы, твердые тела, плазму можно рассматривать как «сплошные», отвлекаясь от их молекулярного и атомарного устройства. Например, при распространении волн в жидкости или газе реальная дискретность этих сред практически не сказывается на свойствах волн, если длина волны многобольше характерного межмолекулярного расстояния. При изучении процесса распространения тепла или диффузии чаще оперируют такими характеристиками как теплоемкость, теплопроводность, скорость диффузии, которые можно обсуждать и практически использовать в технике без выяснения их микроскопической природы. В приближении сплошной среды свойства объекта описываются математически с помощью непрерывных функций от координат и времени: Существующие задачи можно разделить на два класса: статические и динамические. В первом случае значения величин, характеризующих сплошную среду, не зависят от времени, и требуется найти их пространственное распределение. Примеры задач: как распределено в пространстве значение электрического поля, созданного неподвижным точечным зарядом? как распределены электрическое поле в конденсаторе? поле постоянного магнита? скорости в стационарно движущемся по трубе потоке жидкости? Еще сложнее решение динамических задач. Если электрическое поле создается движущимися зарядами, то определить, как оно меняется во времени в каждой точке пространства – очень непростая задача. Не менее трудно определить эволюцию скорости в разных местах в жидкости, если в некотором месте пульсирует давление; изменения значений температуры в разных точках некоторого тела, которое подогревают изнутри или извне от источников тепла, интенсивность которых изменяется со временем. Если поле создается одним точечным зарядом Если поле создано не одним, а несколькими зарядами, то напряженность и потенциал в каждой точке можно найти из принципа суперпозиции:
где Зная потенциал в каждой точке поля, т.е. функцию
В реальных конструкциях поле создается достаточно причудливо расположенными в пространстве заряженными телами самых разных форм: пластины, плоские и изогнутые; штыри; правильные и деформированные сфероиды и т.д. Важно иметь наглядную картину поля, изображенного некоторым условным образом. Существуют два классических способа для наглядного изображения поля: поверхностями (или линиями) равного потенциала и силовыми линиями поля. Для любого электростатического поля множество точек, потенциал в которых одинаков,образует замкнутую поверхность – эквипотенциальную поверхность. Для одного точечного заряда это сфера; в общем случае эта поверхность может быть очень сложной. Линии равного потенциала являются сечениями поверхности равного потенциала той плоскостью, в которой строится изображение. Силовые линии – линии, касательные к которым в каждой точке задают направление вектора напряженности поля. Силовые линии никогда не пересекаются между собой. Они начинаются на положительных зарядах и либо заканчиваются на отрицательных, либо уходят «на бесконечность». По соглашению число силовых линий, исходящих из точечного заряда, пропорционально величине этого заряда; коэфф
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 704; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.229.80 (0.02 с.) |

 , то уравнение движение получается из (2.16) добавлением
, то уравнение движение получается из (2.16) добавлением 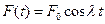 , где
, где  – частота вынужденной силы. В этом случае уравнение движение маятника имеет вид:
– частота вынужденной силы. В этом случае уравнение движение маятника имеет вид: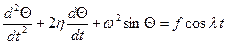 , (2.19)
, (2.19) . При малой амплитуде движения (2.19) примет вид
. При малой амплитуде движения (2.19) примет вид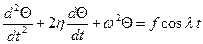 (2.20)
(2.20)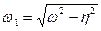 (при
(при  ) и вынужденных колебаний с частотой
) и вынужденных колебаний с частотой  , остаются лишь вынужденные периодические колебания, амплитуда которых зависит от соотношения частот
, остаются лишь вынужденные периодические колебания, амплитуда которых зависит от соотношения частот  и резко возрастает при
и резко возрастает при 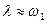 – явление резонанса. Аналитическое решение уравнения (2.20) имеет вид
– явление резонанса. Аналитическое решение уравнения (2.20) имеет вид .
. и
и  – произвольные постоянные, находятся из начальных условий.
– произвольные постоянные, находятся из начальных условий. и
и  могут как проводится простым табулированием формулы (2.21) так и с помощью численного моделирования уравнения (2.20).
могут как проводится простым табулированием формулы (2.21) так и с помощью численного моделирования уравнения (2.20).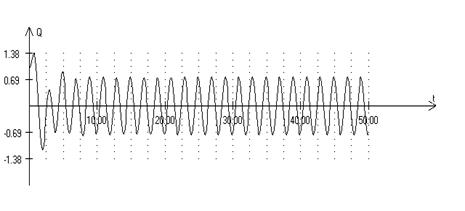



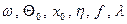 .
.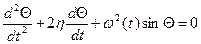 ,
, – заданная функция, определяющая закон изменения частоты. В случае гармонического изменения
– заданная функция, определяющая закон изменения частоты. В случае гармонического изменения 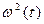 определяется по формуле
определяется по формуле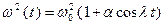 , (2.22)
, (2.22)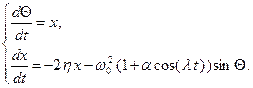
 , а именно
, а именно  ,
, 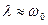 ,
,  ,
,  ,
, 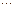 и при определенных значениях величины
и при определенных значениях величины  в системе возникают нарастающие колебания. На рис. 2.8 схематически изображена фазовая диаграмма системы в переменных
в системе возникают нарастающие колебания. На рис. 2.8 схематически изображена фазовая диаграмма системы в переменных  и
и 
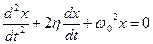 описывает следующие системы: математический маятник; пружинный маятник; «физический» маятник – тело, свободно вращающееся около горизонтальной оси; крутильный маятник наручных часов – симметричное тело, совершающее колебания около вертикальной оси под действием спиральной пружины; ток в колебательном контуре; акустический резонатор Гельмгольца, в котором происходит колебания воздуха в колбе с широким горлышком; колебания магнитной стрелки компаса.
описывает следующие системы: математический маятник; пружинный маятник; «физический» маятник – тело, свободно вращающееся около горизонтальной оси; крутильный маятник наручных часов – симметричное тело, совершающее колебания около вертикальной оси под действием спиральной пружины; ток в колебательном контуре; акустический резонатор Гельмгольца, в котором происходит колебания воздуха в колбе с широким горлышком; колебания магнитной стрелки компаса.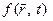 . За каждым «свойством» закрепляется такая функция, и их взаимосвязанный вид дает полное описание среды.
. За каждым «свойством» закрепляется такая функция, и их взаимосвязанный вид дает полное описание среды. ,то величина напряженности поля зависит от расстояния
,то величина напряженности поля зависит от расстояния 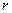 от
от  . Поле существует независимо от пробного заряда
. Поле существует независимо от пробного заряда  и может рассматриваться как сплошная среда. Существуют две взаимосвязанные характеристики электрического поля: напряженность
и может рассматриваться как сплошная среда. Существуют две взаимосвязанные характеристики электрического поля: напряженность  и потенциал
и потенциал  . Для поля точечного заряда
. Для поля точечного заряда 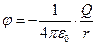 .
. ,
,  ,
, и
и  создаются в этой точке
создаются в этой точке  -м зарядом.
-м зарядом. , можно найти напряженность в каждой точке чисто математическим путем на основании того, что проекция вектора напряженности на любое направление есть скорость изменения потенциала в этом направлении:
, можно найти напряженность в каждой точке чисто математическим путем на основании того, что проекция вектора напряженности на любое направление есть скорость изменения потенциала в этом направлении: ,
,  ,
, 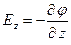 . (2.23)
. (2.23)


