
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 4. Математические модели в экономикеСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
4.1. Классификация экономико-математических методов и моделей. Экономико-математическое моделирование заключается в описании социально-экономических систем и процессов в виде экономико-математических моделей. Экономико-математические методы следует понимать как инструмент, а экономико-математические модели – как продукт процесса экономико-математического моделирования. Классификация экономико-математических методов сводится к классификации научных дисциплин, входящих в их состав. Хотя общепринятая классификация этих дисциплин до конца не выработана, в составе экономико-математических методов можно выделить следующие разделы: 1. Экономическая кибернетика: системный анализ экономики, теория экономической информации и теория управляющих систем; 2. Математическая статистика: экономические приложения данной дисциплины – выборочный метод, дисперсионный анализ, корреляционный анализ, регрессионный анализ, многомерный статистический анализ, факторный анализ, теория индексов и др.; 3. Математическая экономия и изучающая те же вопросы с количественной стороны эконометрия:теория экономического роста, теория производственных функций, межотраслевые балансы, национальные счета, анализ спроса и потребления, региональный и пространственный анализ, глобальное моделирование и др.; 4. Методы принятия оптимальных решений, в том числе исследование операций в экономике: программирование, включая методы ветвей и границ, сетевые методы планирования и управления, программно-целевые методы планирования и управления, теория и методы управления запасами, теория массового обслуживания, теория игр и др.; 5. Методы и дисциплины, специфичные отдельно как для централизованно планируемой экономики, так и для рыночной (конкурентной) экономики. К первым относится теория оптимального функционирования экономики, оптимальное планирование, теория оптимального ценообразования, модели материально-технического снабжения и др. Ко вторым – методы, позволяющие разработать модели свободной конкуренции, модели капиталистического цикла, модели монополии, модели индикативного планирования, модели теории фирмы и т.д. 6. Методы экспериментального изучения экономических явлений. К ним относятся математические методы анализа и планирования экономических экспериментов, методы машинной имитации, деловые игры. Сюда также относят методы экспертных оценок, разработанные для оценки явлений, не поддающихся непосредственному измерению. Существует более 10 основных признаков классификации экономических моделей. Рассмотрим основные из них. По общему целевому назначению экономико-математические модели делятся на теоретико-аналитические, используемые при изучении общих свойств и закономерностей экономических процессов, и прикладные, применяемые в решении конкретных экономических задач анализа, прогнозирования и управления. По степени агрегирования объектов моделирования модели разделяются на макроэкономические и микроэкономические. К первым относят модели, отражающие функционирование экономики как единого целого, микроэкономические модели связаны с такими звеньями экономики как предприятия и фирмы. По цели создания и применения, выделяют балансовые модели, выражающие требование соответствия наличия ресурсов и их использования; трендовые модели, в которых развитие моделируемой экономической системы отражается через длительную тенденцию ее основных показателей; оптимизационные модели, предназначенные для выбора наилучшего варианта из определенного числа вариантов производства, распределения или потребления; имитационные модели, предназначенные для использования в процессе машинной имитации изучаемых систем или процессов. По типу информации, используемой в модели, экономико-математические модели делятся на аналитические, построенные на априорной информации, и идентифицируемые, построенные на апостериорной информации. По учету фактора времени модели подразделяются на статические, в которых все зависимости отнесены к одному моменту времени, и динамические, описывающие экономические системы в развитии. По учету фактора неопределенности модели разделяют на детерминированные, если в них результаты на выходе однозначно определяются управляющими воздействиями, и стохастические (вероятностные), если при задании на входе модели определенной совокупности значений на ее выходе могут получаться различные результаты в зависимости от действия случайного фактора. По характеристике математических объектов, включенных в модель – по типу математического аппарата, используемого в модели. По этому признаку могут быть выделены матричные модели, модели линейного и нелинейного программирования, корреляционно-регрессионные модели, модели теории массового обслуживания, модели сетевого планирования и управления, модели теории игр и т.д. По типу подхода к изучаемым социально-экономическим системам выделяют дескриптивные и нормативные модели. При дескриптивном (описательном) подходе получаются модели, предназначенные для описания и объяснения фактически наблюдаемых явлений или для прогноза этих явлений; в качестве примера дескриптивных моделей можно привести названные ранее балансовые и трендовые модели. При нормативном подходе интересуются не тем, каким образом устроена и развивается экономическая система, а как она должна быть устроена и как должна действовать в смысле определенных критериев. Примером нормативной модели является нормативная модель уровня жизни. 4.2. Балансовый метод. Схема межпродуктового баланса. В основе создания балансовых моделей лежит метод взаимного сопоставления имеющихся материальных, трудовых и финансовых ресурсов и потребностей в них. Если описывать экономическую систему в целом, то под балансовой моделью понимается система уравнений, каждое из которых выражает требование баланса между производимым отдельными экономическими объектами количеством продукции и совокупной потребностью в этой продукции. При таком подходе рассматриваемая система состоит из экономических объектов, каждый из которых выпускает некоторый продукт, часть его потребляется другими объектами системы, а другая часть выводится за пределы системы в качестве ее конечного продукта. Если вместо понятия продукт ввести более общее понятие ресурс, то под балансовой моделью понимают систему уравнений, которые удовлетворяют требованиям соответствия наличия ресурса и его использования. Основные виды балансовых моделей: 1. Частные материальные, трудовые и финансовые балансы для народного хозяйства и отдельных отраслей; 2. Межотраслевые балансы; 3. Матричные техпромфинпланы предприятий и фирм. Балансовый метод и создаваемые на его основе балансовые модели служат основным инструментом поддержания пропорций в народном хозяйстве. Балансовые модели на базе отчетных балансов характеризуют сложившиеся пропорции, в них ресурсная часть всегда равна расходной. Для выявления диспропорций используются балансовые модели, в которых фактические ресурсы сопоставлялись бы не с их фактическим потреблением, а с потребностью в них. Балансовые модели не содержат какого-либо механизма сравнения отдельных вариантов экономических решений и не предусматривают взаимозаменяемости разных ресурсов, что не позволяет сделать выбор оптимального варианта развития экономической системы. Этим определяется ограниченность балансовых моделей и балансового метода в целом [7, 8]. Основу информационного обеспечения балансовых моделей в экономике составляет матрица коэффициентов затрат ресурсов по конкретным направлениям их использования. Например, в модели межотраслевого баланса такую роль играет так называемая технологическая матрица – таблица межотраслевого баланса, составленная из коэффициентов (нормативов) прямых затрат на производство единицы продукции в натуральном выражении. По многим причинам исходные данные реальных хозяйственных объектов не могут быть использованы в балансовых моделях непосредственно, поэтому подготовка информации для ввода в модель является весьма серьезной проблемой. При построении модели межотраслевого баланса используется специфическое понятие чистой (или технологической) отрасли, т.е. условной отрасли, объединяющей все производство данного продукта независимо от ведомственной (административной) подчиненности и форм собственности предприятий и фирм. Переход от хозяйственных отраслей к чистым отраслям требует специального преобразования реальных данных хозяйственных объектов, например, агрегирования отраслей, исключения внутриотраслевого оборота и др. В этих условиях понятия «межпродуктовый баланс» и «межотраслевой баланс» практически идентичны, отличие заключается лишь в единицах измерения элементов баланса. В матричных моделях балансовый метод получает строгое математическое выражение. Матричную структуру имеют межотраслевой и межрайонный балансы производства и распределения продукции в народном хозяйстве, модели развития отраслей, межотраслевые балансы производства и распределения продукции отдельных регионов, модели промфинпланов предприятий и фирм. Несмотря на специфику этих моделей, их объединяет не только общий формальный (матричный) принцип построения и единство системы расчетов, но и аналогичность ряда экономических характеристик. Схема межотраслевого баланса (МОБ) производства и распределения совокупного общественного продукта в стоимостном выражении приведена в таблице 4.1. В основу этой схемы положено разделение совокупного продукта на две части: промежуточный и конечный продукты; все народное хозяйство представлено в виде совокупности Первый квадрант МОБ – это таблица межотраслевых материальных связей. Показатели, помещенные на пересечениях строк и столбцов, представляют собой величины межотраслевых потоков продукции и в общем виде обозначаются Во втором квадранте представлена конечная продукция всех отраслей материального производства, при этом под конечной понимается продукция, выходящая из сферы производства в область конечного использования (на потребление и накопление). В таблице 4.1 этот раздел представлен в виде одного столбца величин Третий квадрант МОБ характеризует национальный доход, со стороны его стоимостного состава как сумму чистой продукции и амортизации; чистая продукция понимается при этом как сумма оплаты труда и чистого дохода отраслей. Сумму амортизации ( Четвертый квадрант баланса находится на пересечении столбцов второго квадранта (конечной продукции) и строк третьего квадранта (условно чистой продукции). Этим определяется содержание квадранта: он отражает конечное распределение и использование национального дохода. В результате перераспределения первоначально созданного национального дохода образуются конечные доходы населения, предприятий, государства. Данные четвертого квадранта важны для отражения в межотраслевой модели баланса доходов и расходов населения, источников финансирования капиталовложений, текущих затрат непроизводственной сферы, для анализа общей структуры конечных доходов по группам потребителей.
Таблица 4.1. Схема межотраслевого баланса В целом межотраслевой баланс в рамках единой модели объединяет балансы отраслей материального производства, баланс совокупного общественного продукта, балансы национального дохода, финансовый, баланс доходов и расходов населения. Если обозначить валовой продукт некоторой отрасли буквой Рассматривая схему баланса по столбцам получаем что итог материальных затрат любой потребляющей отрасли и ее условно чистой продукции равен валовой продукции этой отрасли:
Рассматривая схему МОБ по строкам для каждой производящей отрасли, получаем, что валовая продукция
Формула (4.2) описывает систему из Суммируя по всем отраслям уравнения (4.1), получим
Аналогичное суммирование уравнения (4.2) дает
Левые части обоих равенств равны, так как представляют собой весь валовой общественный продукт. Первые слагаемые правых частей этих равенств также равны, их величина равна итогу первого квадранта. Следовательно, должно выполняться соотношение
Уравнение (4.3) показывает, что в межотраслевом балансе соблюдается важнейший принцип единства материального и стоимостного состава национального дохода. Рассмотрим схему получения технологической матрицы. Предполагается, что для производства единицы продукции в
Коэффициент прямых материальных затрат показывает, какое количество продукции С учетом формулы (4.4) система уравнений баланса (4.2) примет вид
В матрично-векторном обозначении система (4.5) имеет вид
Система уравнений (4.6) называется экономико-математической моделью межотраслевого баланса (моделью Леонтьева, моделью «затраты – выпуск»). С помощью этой модели можно выполнять три варианта расчетов: 1. Задав в модели величины валовой продукции каждой отрасли
2. Задав величины конечной продукции всех отраслей
3. Из соотношения (4.8) следует, что
где коэффициенты Коэффициенты полных материальных затрат можно применять, когда необходимо определить, как скажется на валовом выпуске некоторой отрасли предполагаемое изменение объемов конечной продукции всех отраслей
где 4.3. Коэффициенты прямых и полных материальных затрат. Коэффициенты прямых затрат по определению неотрицательны, следовательно, матрица Система уравнений межотраслевого баланса является отражением реальных экономических процессов, в которых содержательный смысл могут иметь лишь неотрицательные значения валовых выпусков – Неотрицательная матрица
Условие (4.10) означает, что существует положительный вектор конечной продукции Для того чтобы матрица коэффициентов прямых материальных затрат 1) для матрицы 2) матричный ряд 3) наибольшее по модулю собственное значение
строго меньше единицы; 4) все главные миноры матрицы Более простым, но только достаточным признаком продуктивности матрицы Существует ещё одно определение коэффициента полных материальных затрат исходя из того, что кроме прямых затрат существуют косвенные затраты той или иной продукции при производстве продукции данной отрасли. Рассмотрим пример формирования затрат электроэнергии на выпуск стального проката, при этом ограничимся технологической цепочкой «руда – чугун – сталь – прокат». Затраты электроэнергии при получении проката из стали будут называться прямыми затратами, те же затраты при получении стали из чугуна называются косвенными затратами 1-го порядка, а затраты электроэнергии при получении чугуна из руды называются косвенными затратами электроэнергии на выпуск стального проката 2-го порядка и т.д. Коэффициентом полных материальных затрат
Если ввести в рассмотрение матрицу коэффициентов полных материальных затрат
Исходя из содержательного смысла коэффициентов косвенных материальных затрат имеют место соотношения
С учетом последних соотношений формула (4.12) примет вид
Из второго уравнения продуктивности следует, что существует матрица
Сопоставляя соотношения (4.13), (4.14) получаем связь между двумя матрицами коэффициентов полных материальных затрат
или, в поэлементной записи:
В отличие от коэффициентов матрицы 4.4. Межотраслевые балансовые модели в анализе экономических показателей. Различные модификации рассмотренной выше модели межотраслевого баланса производства и распределения продукции в народном хозяйстве позволяют расширить круг показателей, охватываемых моделью. Рассмотрим применение межотраслевого балансового метода для анализа таких важных экономических показателей, как труд, фонды и цены. К числу важнейших аналитических возможностей данного метода относится определение прямых и полных затрат труда на единицу продукции и разработка на этой основе балансовых продуктово-трудовых моделей, исходной моделью при этом служит отчетный межпродуктовый баланс в натуральном выражении. В этом балансе по строкам представлено распределение каждого отдельного продукта на производство других продуктов и конечное потребление (первый и второй квадранты схемы межотраслевого баланса). Отдельной строкой дается распределение затрат живого труда в производстве всех видов продукции; предполагается, что трудовые затраты выражены в единицах труда одинаковой степени сложности. Обозначим затраты живого труда в производстве
Введем понятие полных затрат труда как суммы прямых затрат живого труда и затрат овеществленного труда, перенесенных на продукт через израсходованные средства производства. Если обозначить величину полных затрат труда на единицу продукции
или в матрично-векторных обозначениях
Из (4.16) с очевидностью следует соотношение для вектора коэффициентов полной трудоемкости
Обозначим через
На основе соотношений (4.9), (4.17) следует равенство
где Соотношение (4.19) представляет собой основное балансовое равенство в теории межотраслевого баланса труда. Экономическое содержание (4.19) заключается в том, что стоимость конечной продукции, оцененной по полным затратам труда, равна совокупным затратам живого труда. Сопоставляя потребительский эффект различных взаимозаменяемых продуктов с полными трудовыми затратами на их выпуск, можно судить о сравнительной эффективности их производства. С помощью показателей полной трудоемкости более полно и точно, чем при использовании существующих стоимостных показателей, выявляется структура затрат на выпуск различных видов продукции и прежде всего соотношение между затратами живого и овеществленного труда. На основе коэффициентов прямой и полной трудоемкости могут быть разработаны межотраслевые и межпродуктовые балансы затрат труда и использования трудовых ресурсов. Схематически эти балансы строятся по общему типу матричных моделей, однако все показатели в них (межотраслевые связи, конечный продукт, условно чистая продукция и др.) выражены в трудовых измерителях. Развитие основной модели межотраслевого баланса достигается также путем включения в нее показателей фондоемкости продукции. В простейшем случае модель дополняется отдельной строкой, в которой указаны в стоимостном выражении объемы производственных фондов
Коэффициент прямой фондоемкости показывает величину производственных фондов, непосредственно занятых в производстве данной отрасли, в расчете на единицу ее валовой продукции. В отличие от этого показателя коэффициент полной фондоемкости
В матричной форме (4.21) имеет вид
или Для более глубокого анализа необходимо дифференцировать фонды на основные и оборотные, а в пределах основных – на здания, сооружения, производственное оборудование, транспортные средства и т.д. Пусть в целом все производственные фонды разделены на
где Коэффициенты прямой фондоемкости также образуют матрицу размерности
Для каждой
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 отраслей, при этом каждая отрасль фигурирует в балансе как производящая и как потребляющая.
отраслей, при этом каждая отрасль фигурирует в балансе как производящая и как потребляющая. , где
, где  и
и 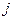 – соответственно номера отраслей производящих и потребляющих. Например, величина
– соответственно номера отраслей производящих и потребляющих. Например, величина  понимается как стоимость средств производства, произведенных в отрасли с номером 3 и потребленных в качестве материальных затрат в отрасли с номером 2. Таким образом, первый квадрант по форме представляет собой квадратную матрицу порядка
понимается как стоимость средств производства, произведенных в отрасли с номером 3 и потребленных в качестве материальных затрат в отрасли с номером 2. Таким образом, первый квадрант по форме представляет собой квадратную матрицу порядка  .
. ) и чистой продукции (
) и чистой продукции ( ) некоторой
) некоторой  .
.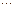








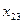

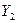


















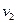







 , где
, где  ,
,  . (4.1)
. (4.1) ,
,  . (4.2)
. (4.2) .
. .
. . (4.3)
. (4.3) . Оно не зависит от объема производства в отрасли и является стабильной величиной во времени. Величины
. Оно не зависит от объема производства в отрасли и является стабильной величиной во времени. Величины  ,
,  . (4.4)
. (4.4) ,
,  . (4.5)
. (4.5)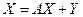 . (4.6)
. (4.6)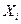 можно определить объемы конечной продукции каждой отрасли
можно определить объемы конечной продукции каждой отрасли  . (4.7)
. (4.7) . (4.8)
. (4.8) ,
,  , или
, или  , (4.9)
, (4.9) показывают, сколько нужно произвести продукции
показывают, сколько нужно произвести продукции  ,
, ,
,  – изменения величин валовой и конечной продукции соответственно.
– изменения величин валовой и конечной продукции соответственно. в целом неотрицательна:
в целом неотрицательна:  . Так как процесс воспроизводства нельзя осуществлять, если для собственного воспроизводства в отрасли затрачивается большее количество продукта, чем создается, то диагональные элементы матрицы
. Так как процесс воспроизводства нельзя осуществлять, если для собственного воспроизводства в отрасли затрачивается большее количество продукта, чем создается, то диагональные элементы матрицы  .
. ; Актуальным является вопрос, при каких условиях экономическая система способна обеспечить положительный конечный выпуск по всем отраслям. Ответ на него связан с понятием продуктивности матрицы коэффициентов прямых материальных затрат.
; Актуальным является вопрос, при каких условиях экономическая система способна обеспечить положительный конечный выпуск по всем отраслям. Ответ на него связан с понятием продуктивности матрицы коэффициентов прямых материальных затрат. , что
, что . (4.10)
. (4.10) для модели межотраслевого баланса (4.6).
для модели межотраслевого баланса (4.6). существует неотрицательная обратная матрица
существует неотрицательная обратная матрица  ;
; сходится, и его сумма равна обратной матрице
сходится, и его сумма равна обратной матрице  матрицы
матрицы  ,
, называется сумма прямых затрат и косвенных затрат продукции
называется сумма прямых затрат и косвенных затрат продукции  -гопорядка обозначить через
-гопорядка обозначить через  ,то имеет место формула
,то имеет место формула . (4.11)
. (4.11) и матрицы коэффициентов косвенных материальных затрат различных порядков
и матрицы коэффициентов косвенных материальных затрат различных порядков  , то поэлементную формулу (4.11) можно записать в виде
, то поэлементную формулу (4.11) можно записать в виде . (4.12)
. (4.12) ,
,  , …,
, …,  .
. . (4.13)
. (4.13) , являющаяся суммой сходящегося матричного ряда
, являющаяся суммой сходящегося матричного ряда . (4.14)
. (4.14) ,
,
 включают в себя кроме затрат также саму единицу конечной продукции, которая выходит за сферу производства.
включают в себя кроме затрат также саму единицу конечной продукции, которая выходит за сферу производства. , а объем производства этого продукта (валовой выпуск), как и раньше, через
, а объем производства этого продукта (валовой выпуск), как и раньше, через  ,
,  . (4.15)
. (4.15)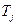 ,то произведения вида
,то произведения вида  отражают затраты овеществленного труда, перенесенного на «единицу
отражают затраты овеществленного труда, перенесенного на «единицу  ,
,  ,
, . (4.16)
. (4.16) или
или  . (4.17)
. (4.17) величину совокупности затрат живого труда по всем видам продукции, которая с учетом формулы (4.15) будет равна
величину совокупности затрат живого труда по всем видам продукции, которая с учетом формулы (4.15) будет равна . (4.18)
. (4.18) , (4.19)
, (4.19) и
и  – вектор-строки коэффициентов прямой и полной трудоемкости, а
– вектор-строки коэффициентов прямой и полной трудоемкости, а 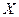 и
и  – вектор столбцы валовой и конечной продукции.
– вектор столбцы валовой и конечной продукции. , занятые в каждой
, занятые в каждой  ,
, 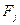 отражает объем фондов, необходимых во всех отраслях для выпуска единицы конечной продукции
отражает объем фондов, необходимых во всех отраслях для выпуска единицы конечной продукции 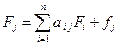 ,
,  , (4.22)
, (4.22)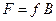 .
. групп. Тогда характеристика занятых в народном хозяйстве фондов задается матрицей показателей
групп. Тогда характеристика занятых в народном хозяйстве фондов задается матрицей показателей ,
, отражает объем фондов
отражает объем фондов  , элементы которой определяют величину производственных фондов
, элементы которой определяют величину производственных фондов  .
. , отражающие полную потребность в фондах
, отражающие полную потребность в фондах  ,
, 


