Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 3. Моделирование в экологииСодержание книги Поиск на нашем сайте
Введем следующие понятия. Особь – это отдельный индивидуум, отдельный организм. Популяция – это совокупность особей одного вида, существующих в одно и то же время и занимающих определенную территорию. Сообщество – это совокупность совместно сосуществующих популяций. В классической экологии рассматриваются взаимодействия следующих типов: • взаимодействие организма и окружающей среды; • взаимодействие особей внутри популяции; • взаимодействие между особями разных видов (между популяциями). Математические модели в экологии используются практически с момента возникновения этой науки. Они помогают установить некоторые закономерности и общие тенденции развития отдельных популяций, а также сообществ. Основными целями создания математических моделей в экологии являются следующие: 1. Выделить суть или объединить и выразить с помощью нескольких параметров важные разрозненные свойства большого числа уникальных наблюдений, чтобы облегчить экологу анализ рассматриваемого процесса или проблемы. 2. Описать каждое уникальное явление, и относительные свойства таких явлений. 3. Создать «идеальный объект» или идеализированное поведение, при сравнении с которым можно оценивать и измерять реальные объекты и процессы. При построении моделей в математической экологии используется опыт математического моделирования механических и физических систем, с учетом специфических особенностей биологических систем: • сложности внутреннего строения каждой особи; • зависимости условий жизнедеятельности организмов от многих факторов внешней среды; • незамкнутости экологических систем; • огромного диапазона внешних характеристик, при которых сохраняется жизнеспособность систем. 3.1. Моделирование внутривидовой конкуренции. Рассмотрим простейшую модель для вида с дискретным периодом размножения, в которой численность популяции в момент времени
решение которого имеет вид Конкуренцию можно определить как использование некоего ресурса (пищи, воды, света, пространства) каким либо организмом, который тем самым уменьшает доступность этого ресурса для других организмов. Если конкурирующие организмы принадлежат к одному виду, то взаимоотношения между ними называют внутривидовой конкуренцией; если же они относятся к разным видам, то их взаимоотношения называют межвидовой конкуренцией.
Рис. 3.1. Изменение скорости роста популяции На рис. 3.1 показана возможная зависимость скорости воспроизводства от численности популяции. Точка В преобразованном виде оно выглядит так:
Точка
где
Рис. 3.2. Изменение численности популяции согласно уравнению (3.2) при После несложного изменения в уравнении (3.2) может быть получена более общая модель, учитывающая интенсивность конкуренции. Простейшая из возможных зависимостей падения скорости роста популяции от ее численности, изображенная на рис. 3.1, является не законом природы, а всего лишь удобной гипотезой. Далеко не всегда реальная динамика численности популяции, определяемая внутривидовой конкуренцией, даже качественно согласуется с изображенной на рис. 3.2. Более общая гипотеза о законе падения скорости роста популяции в зависимости от ее численности приводит к следующему уравнению:
Общность данной модели в отличие от уравнения (3.2) обусловлена введением в модель параметра Ниже представлен код программы, моделирующей уравнение (3.3) при заданных значениях параметров. program con_disk; uses crt,graph; const u1=200; u2=600; v1=80; v2=380; a=0; b=20; h=1; k0=200; n_0=20; str_tt='t='; str_nn='n='; { r=2; bb=1; } { r=2; bb=1.4; } { r=2; bb=3.9; } { r=4; bb=3.6; } r=4; bb=4.4; var adapter,regim,i,k,tmax,nmax,d:integer; kt,kn,t,aa:extended; u_n,v_n,u1_n,v1_n:longint; x,y,x_1,x_2,y_1,y_2:longint; n0,n,n_max,t_max:extended; str_1,str_t,str_n:string; begin clrscr; adapter:=detect; initgraph(adapter,regim,'d:\lang\bp\bgi'); n0:=n_0; t:=a; n_max:=n0; aa:=(r-1)/k0; repeat t:=t+h; n:=(r*n0)/(1+exp(bb*ln(aa*n0))); if n>n_max then n_max:=n; if n<1 then n:=0; n0:=n; until t>=b-h; t_max:=b; tmax:=round(t_max); nmax:=round(n_max); if tmax mod 10<>0 then tmax:=round(t_max)+(10-(round(t_max) mod 10)); if nmax mod 10<>0 then nmax:=round(n_max)+(10-(round(n_max) mod 10)); kt:=10*(u2-u1)/(11*tmax); kn:=10*(v2-v1)/(11*nmax); setcolor(white); line(u1,v2,u1,v1); line(u1,v2,u2,v2); line(u1-5,v1+10,u1,v1); line(u1+5,v1+10,u1,v1); line(u2-10,v2-5,u2,v2); line(u2-10,v2+5,u2,v2); outtextxy(u1-20,v1,'N'); outtextxy(u1-10,v2,'O'); outtextxy(u2,v2+10,'t'); for i:=1 to 10 do begin y:=round(v2-(i*(v2-v1)/11)); x_1:=u1-5; x_2:=u1+5; line(x_1,y,x_2,y); str(i*nmax/10:3:0,str_1); outtextxy(u1-40,y,str_1); end; for i:=1 to 10 do begin x:=round(u1+(i*(u2-u1)/11)); y_1:=v2-5; y_2:=v2+5; line(x,y_1,x,y_2); str(i*tmax/10:2:0,str_1); outtextxy(x-10,v2+10,str_1); end; t:=a; n0:=n_0; k:=0; d:=0; u_n:=round(u1+kt*t); v_n:=round(v2-kn*n0); repeat t:=t+h; n:=(r*n0)/(1+exp(bb*ln(aa*n0))); if n<1 then n:=0; k:=k+1; if k=round(t_max/(20*h)) then begin setcolor(red); str(t:2:0,str_t); str(n:3:0,str_n); outtextxy(20,50+d,str_tt+str_t); outtextxy(90,50+d,str_nn+str_n); d:=d+20; k:=0; end; u1_n:=round(u1+kt*t); v1_n:=round(v2-kn*n); setcolor(blue); line(u_n,v_n,u1_n,v1_n); u_n:=u1_n; v_n:=v1_n; n0:=n; until t>=b; readln; closegraph; end. На рис. 3.3, а, б, в и г, построенных с помощью численного моделирования, показаны различные варианты динамики численности популяций, полученные с помощью уравнения (3.3) при разном сочетании параметров
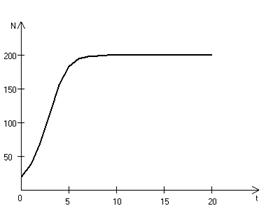
Рис. 3.3, а. Монотонное установление стационарной численности популяции при
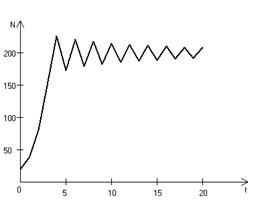
Рис. 3.3, б. Колебательное установление стационарной численности популяции при
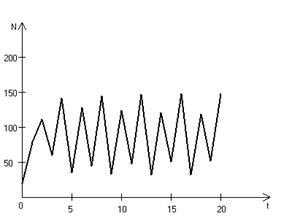
Рис. 3.3, в. Устойчивые предельные циклы изменения численности популяции при
Рис. 3.3, г. Случайные изменения численности популяции при Важной частью исследования, связанного с моделью (3.3), является построение на фазовой плоскости
Рис. 3.4. Схематическое изображение фазовой диаграммы динамики численности популяции с дискретным размножением Для этого надо зафиксировать значения Для уравнений (3.2), (3.3) имеет место, следующее замечание, справедливое для всех моделей в экологии. В отличие от физики, где «модель» часто является точно установленным законом природы, в экологии модель гораздо более условна. Её адекватность реальности проверяется лишь экспериментально. Поскольку экологи много раз наблюдали каждую из динамик, изображенных на рис. 3.3, можно сделать вывод о полезности соответствующей модели. Модели (3.2), (3.3), применимы к популяциям с дискретными периодами размножения. Однако в природе встречаются и популяции, где рождение и гибель организмов происходит непрерывно; для таких популяций модели, выраженные уравнениями из предыдущего пункта, непригодны. Рассмотрим популяцию с непрерывным размножением и построим модель изменения ее численности. Математическим аппаратом в этом случае являются дифференциальные уравнения. Скорость роста обозначается Без учета внутривидовой конкуренции получаем справедливо равенство
где Далее учтем внутривидовую конкуренцию (рис. 3.5).
Рис. 3.5. Зависимость скорости воспроизводства от численности популяции
Когда численность популяции близка к нулю, скорость роста определяется величиной Записав уравнение прямой АВ, получим
Уравнение (3.5) называется «логистическим». Одно из его достоинств – простота. Уравнение относится к одному из стандартных типов и допускает аналитическое решение:
В истории экологии логистическое уравнение сыграло значительную роль, оказав большое влияние на применение в экологии математических методов. С другой стороны, простота уравнения накладывает ограничения на область его применения, так как с его помощью можно описать немногие реальные популяции. Но, несмотря на все ограничения, логистическое уравнение используется как составная часть и в других моделях динамики численности популяций [3, 6]. Код программной модели, позволяющей находить численность популяции, изменяющейся согласно (3.5) имеет вид: program con_nepr; uses crt,graph; const u1=200; u2=630; v1=80; v2=380; a=0; b=3; h=0.001; k0=200; n0=25; str_tt='t='; str_nn='n='; r=3; var adapter,regim,i,k,tmax,nmax,d:integer; kt,kn,t:extended; u_n,v_n,u1_n,v1_n:longint; x,y,x_1,x_2,y_1,y_2:longint; n,n_max,t_max:extended; str_1,str_t,str_n:string; function nt(n:extended):extended; begin nt:=r*n*(k0-n)/k0; end; begin clrscr; adapter:=detect; initgraph(adapter,regim,'d:\lang\bp\bgi'); n:=n0; t:=a; n_max:=n0; repeat t:=t+h; n:=n+h*nt(n); if n>n_max then n_max:=n; if n<1 then n:=0; until t>=b-h; t_max:=b; tmax:=round(t_max); nmax:=round(n_max); if tmax mod 3<>0 then tmax:=round(t_max)+(3-(round(t_max) mod 3)); if nmax mod 10<>0 then nmax:=round(n_max)+(10-(round(n_max) mod 10)); kt:=3*(u2-u1)/(4*tmax); kn:=10*(v2-v1)/(11*nmax); setcolor(white); line(u1,v2,u1,v1); line(u1,v2,u2,v2); line(u1-5,v1+10,u1,v1); line(u1+5,v1+10,u1,v1); line(u2-10,v2-5,u2,v2); line(u2-10,v2+5,u2,v2); outtextxy(u1-20,v1,'N'); outtextxy(u1-10,v2,'O'); outtextxy(u2,v2+10,'t'); for i:=1 to 10 do begin y:=round(v2-(i*(v2-v1)/11)); x_1:=u1-5; x_2:=u1+5; line(x_1,y,x_2,y); str(i*nmax/10:3:0,str_1); outtextxy(u1-40,y,str_1); end; for i:=1 to 3 do begin x:=round(u1+(i*(u2-u1)/4)); y_1:=v2-5; y_2:=v2+5; line(x,y_1,x,y_2); str(i*tmax/3:2:0,str_1); outtextxy(x-10,v2+10,str_1); end; t:=a; n:=n0; k:=0; d:=0; u_n:=round(u1+kt*t); v_n:=round(v2-kn*n0); repeat t:=t+h; n:=n+h*nt(n); if n<1 then n:=0; k:=k+1; if k=round(t_max/(20*h)) then begin setcolor(red); str(t:5:2,str_t); str(n:3:0,str_n); outtextxy(10,50+d,str_tt+str_t); outtextxy(90,50+d,str_nn+str_n); d:=d+20; k:=0; end; u1_n:=round(u1+kt*t); v1_n:=round(v2-kn*n); setcolor(blue); line(u_n,v_n,u1_n,v1_n); u_n:=u1_n; v_n:=v1_n; until t>=b; readln; closegraph; end. На рис. 3.6 представлено изменение численности популяции в соответствии с формулами (3.5), (3.6).
Рис. 3.6. Динамика численности популяции при 3.2. Логистическая модель межвидовой конкуренции. Сущность межвидовой конкуренции заключается в том, что у особей одного вида уменьшается плодовитость, выживаемость и скорость роста в результате использования того же ресурса, что и особями другого вида, причем влиянию конкуренции в той или иной мере подвергаются особи обоих видов. Введем следующие обозначения: Учтем в логистическом уравнении (3.5) межвидовую конкуренцию следующим образом: предположим, что
Численное моделирование системы (3.7) реализует следующая программа:
program con_mesh; uses crt,graph; const u1=260; u2=630; v1=90; v2=370; a=0; b=3; h=0.001; k1=200; k2=180; n01=100; n02=25; str_tt='t='; str_nn1='n1='; str_nn2='n2='; r1=2; r2=4; a1=0.5; a2=0.65; var adapter,regim,i,k,tmax,nmax,d:integer; kt,kn,t:extended; x1_n1,y1_n1,x2_n1,y2_n1:longint; x1_n2,y1_n2,x2_n2,y2_n2:longint; x,y,x_1,x_2,y_1,y_2:longint; n1,n2,n0,n_max,t_max:extended; str_1,str_t,str_n1,str_n2:string; function n1t(n1,n2:extended):extended; begin n1t:=r1*n1*(k1-n1-(a1*n2))/k1; end; function n2t(n1,n2:extended):extended; begin n2t:=r2*n2*(k2-n2-(a2*n1))/k2; end; begin clrscr; adapter:=detect; initgraph(adapter,regim,'d:\lang\bp\bgi'); n1:=n01; n2:=n02; t:=a; if n1>n2 then n_max:=n1 else n_max:=n2; repeat t:=t+h; n0:=n1; n1:=n1+h*n1t(n1,n2); n2:=n2+h*n2t(n0,n2); if n1>n_max then n_max:=n1; if n2>n_max then n_max:=n2; if n1<1 then n1:=0; if n2<1 then n2:=0; until t>=b-h; t_max:=b; tmax:=round(t_max); nmax:=round(n_max); if tmax mod 3<>0 then tmax:=round(t_max)+(3-(round(t_max) mod 3)); if nmax mod 10<>0 then nmax:=round(n_max)+(10-(round(n_max) mod 10)); kt:=3*(u2-u1)/(4*tmax); kn:=10*(v2-v1)/(11*nmax); setcolor(white); line(u1,v2,u1,v1); line(u1,v2,u2,v2); line(u1-5,v1+10,u1,v1); line(u1+5,v1+10,u1,v1); line(u2-10,v2-5,u2,v2); line(u2-10,v2+5,u2,v2); outtextxy(u1-45,v1,'N1,N2'); outtextxy(u1-10,v2,'O'); outtextxy(u2,v2+10,'t'); for i:=1 to 10 do begin y:=round(v2-(i*(v2-v1)/11)); x_1:=u1-5; x_2:=u1+5; line(x_1,y,x_2,y); str(i*nmax/10:3:0,str_1); outtextxy(u1-40,y,str_1); end; for i:=1 to 3 do begin x:=round(u1+(i*(u2-u1)/4)); y_1:=v2-5; y_2:=v2+5; line(x,y_1,x,y_2); str(i*tmax/3:2:0,str_1); outtextxy(x-10,v2+10,str_1); end; t:=a; n1:=n01; n2:=n02; k:=0; d:=0; x1_n1:=round(u1+kt*t); y1_n1:=round(v2-kn*n1); x1_n2:=round(u1+kt*t); y1_n2:=round(v2-kn*n2); repeat t:=t+h; n0:=n1; n1:=n1+h*n1t(n1,n2); n2:=n2+h*n2t(n0,n2); if n1<1 then n1:=0; if n2<1 then n2:=0; k:=k+1; if k=round(t_max/(20*h)) then begin setcolor(red); str(t:5:2,str_t); str(n1:3:0,str_n1); str(n2:3:0,str_n2); outtextxy(10,50+d,str_tt+str_t); outtextxy(90,50+d,str_nn1+str_n1); outtextxy(160,50+d,str_nn2+str_n2); d:=d+20; k:=0; end; x2_n1:=round(u1+kt*t); y2_n1:=round(v2-kn*n1); setcolor(blue); line(x1_n1,y1_n1,x2_n1,y2_n1); x2_n2:=round(u1+kt*t); y2_n2:=round(v2-kn*n2); setcolor(green); line(x1_n2,y1_n2,x2_n2,y2_n2); x1_n1:=x2_n1; y1_n1:=y2_n1; x1_n2:=x2_n2; y1_n2:=y2_n2; until t>=b; readln; closegraph; end. Модель межвидовой конкуренции, выраженная системой (3.7), названа в честь ее авторов «моделью Лотки-Вольтерры». Если коэффициенты Устойчивое сосуществование достигается лишь при
Рис. 3.7. Устойчивое сосуществование популяций при Основной вопрос, который интересует исследователя межвидовой конкуренции – при каких условиях увеличивается или уменьшается численность каждого вида? Для ответа на этот вопрос надо построить диаграммы, где изображены все возможные сочетания численностей обоих видов. На таких диаграммах численность одного вида откладывают по горизонтальной оси, а другого – по вертикальной. При одних сочетаниях численностей будет отмечаться рост выбранной для наблюдения популяции, при других – уменьшение ее численности. Также для каждого из видов можно провести изоклины – линии, вдоль которых не наблюдается ни увеличения, ни уменьшения численности. Рассмотрим, как можно построить изоклину для первого вида. По определению, для этой линии
Рис. 3.8. Изоклины, полученные с помощью модели Лотки-Вольтерры Длины стрелок пропорциональны изменению численности, стрелки указывают направление изменения численности. Полученное уравнение изоклины является уравнением прямой в плоскости
Рис. 3.9. Результаты конкуренции, полученные с помощью модели Лотки-Вольтерры при различных параметрах Для решения поставленной выше задачи объединим в одной фазовой плоскости изоклины для обоих видов и будем одновременно исследовать динамику их численности. Изоклины относительно друг друга располагаются четырьмя различными способами, что дает различный исход конкуренции. На рисунке 3.9 а) в зоне I численность обеих популяций падает; в зоне II – численность первой популяции растет, второй – уменьшается; в зоне III – численность обеих популяций увеличивается.
3.3. Динамика численности популяций хищника и жертвы. Рассматривая динамику численности популяций хищника и жертвы, экологи прежде всего стремятся понять ее закономерности и разъяснить различия между типами динамик. В простейших моделях хищник и жертва рассматриваются безотносительно влияния на них других видов. Одна из самых первых и простых моделей была предложена, как и модель межвидовой конкуренции, Лоткой и Вольтеррой, и носит их имя. Модель состоит из двух компонентов: Предполагается, что в отсутствие хищника популяция жертвы растет экспоненциально. Чем больше численность той и другой популяции, тем чаще происходят встречи. Число встреченных и съеденных жертв будет зависеть от эффективности, с которой хищник находит и ловит жертву. Если обозначить через
В отсутствие пищи отдельные особи хищника голодают и гибнут. Предполагается, что численность хищника в отсутствие пищи будет уменьшаться экспоненциально:
Так как процессы рассматриваются вместе, уравнения объединяются в систему:
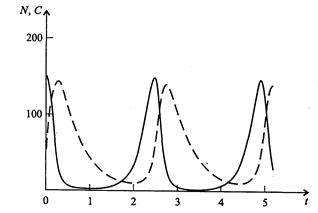
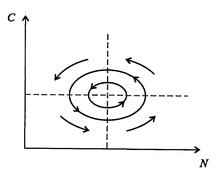
Ниже представлен код программы, на основе которой численно моделируется система (3.8) и графически иллюстрируется динамика изменения численности популяций. program model; uses crt,graph; const u1=260; u2=630; v1=90; v2=370; a=0; b=5; h=0.001; n_0=150; c_0=50; str_tt='t='; str_nn='n='; str_cc='c='; r=5; aa=0.1; q=2; f=0.6; var adapter,regim,i,k,tmax,ncmax,d:integer; kt,knc,t:extended; x1_n,y1_n,x2_n,y2_n:longint; x1_c,y1_c,x2_c,y2_c:longint; x,y,x_1,x_2,y_1,y_2:longint; n,c,n0,nc_max,t_max:extended; str_1,str_t,str_n,str_c:string; function nt(n,c:extended):extended; begin nt:=r*n-(aa*c*n); end; function ct(n,c:extended):extended; begin ct:=f*aa*c*n-(q*c); end; begin clrscr; adapter:=detect; initgraph(adapter,regim,'d:\lang\bp\bgi'); n:=n_0; c:=c_0; t:=a; if n>c then nc_max:=n else nc_max:=c; repeat t:=t+h; n0:=n; n:=n+h*nt(n,c); c:=c+h*ct(n0,c); if n>nc_max then nc_max:=n; if c>nc_max then nc_max:=c; if n<1 then n:=0; if c<1 then c:=0; until t>=b-h; t_max:=b; tmax:=round(t_max); ncmax:=round(nc_max); if tmax mod 5<>0 then tmax:=round(t_max)+(5-(round(t_max) mod 5)); if ncmax mod 10<>0 then ncmax:=round(nc_max)+(10-(round(nc_max) mod 10)); kt:=5*(u2-u1)/(6*tmax); knc:=10*(v2-v1)/(11*ncmax); setcolor(white); line(u1,v2,u1,v1); line(u1,v2,u2,v2); line(u1-5,v1+10,u1,v1); line(u1+5,v1+10,u1,v1); line(u2-10,v2-5,u2,v2); line(u2-10,v2+5,u2,v2); outtextxy(u1-35,v1,'N,C'); outtextxy(u1-10,v2,'O'); outtextxy(u2,v2+10,'t'); for i:=1 to 10 do begin y:=round(v2-(i*(v2-v1)/11)); x_1:=u1-5; x_2:=u1+5; line(x_1,y,x_2,y); str(i*ncmax/10:3:0,str_1); outtextxy(u1-40,y,str_1); end; for i:=1 to 5 do begin x:=round(u1+(i*(u2-u1)/6)); y_1:=v2-5; y_2:=v2+5; line(x,y_1,x,y_2); str(i*tmax/5:2:0,str_1); outtextxy(x-10,v2+10,str_1); end; t:=a; n:=n_0; c:=c_0; k:=0; d:=0; x1_n:=round(u1+kt*t); y1_n:=round(v2-knc*n); x1_c:=round(u1+kt*t); y1_c:=round(v2-knc*c); repeat t:=t+h; n0:=n; n:=n+h*nt(n,c); c:=c+h*ct(n,c); if n<1 then n:=0; if c<1 then c:=0; k:=k+1; if k=round(t_max/(20*h)) then begin setcolor(blue); str(t:5:2,str_t); str(n:3:0,str_n); str(c:3:0,str_c); outtextxy(10,50+d,str_tt+str_t); outtextxy(90,50+d,str_nn+str_n); outtextxy(160,50+d,str_cc+str_c); d:=d+20; k:=0; end; x2_n:=round(u1+kt*t); y2_n:=round(v2-knc*n); setcolor(green); line(x1_n,y1_n,x2_n,y2_n); x2_c:=round(u1+kt*t); y2_c:=round(v2-knc*c); setcolor(red); line(x1_c,y1_c,x2_c,y2_c); x1_n:=x2_n; y1_n:=y2_n; x1_c:=x2_c; y1_c:=y2_c; until t>=b; readln; closegraph; end. Свойства этой модели можно исследовать, построив изоклины. Для жертвы имеем Соответствующее уравнение изоклины для популяции хищника имеет вид Если поместить обе изоклины на одном рисунке, получим картину взаимодействия популяций (рис. 3.10). Как видно на рис. 3.10, численности популяций хищника и жертвы совершают периодические колебания: при увеличении численности хищников уменьшается численность популяции жертвы и наоборот. Такие колебания численности будут продолжаться в соответствии с моделью до тех пор, пока какое-либо внешнее воздействие не изменит численность популяций, после чего произойдет переход в новое устойчивое состояние (такая ситуация называется «нейтральные устойчивые циклы»).
Рис. 3.10. Фазовый портрет системы На рис. 3.11 представлена динамика численности популяций при следующих значениях входных параметров –
Рис. 3.11. Динамика численности популяции хищника и жертвы
Вопросы для самоконтроля
1. В чем отличие классической экологии от современной? 2. Какие проблемы рассматриваются в классической экологии? 3. Какие виды взаимодействия организмов принято рассматривать в классической экологии? 4. Какие основные цели построения математических моделей в экологии? 5. В чем отличие биологических систем от физических и механических? 6. Что понимается под конкуренцией в биологии? Внутривидовой конкуренции? Межвидовой конкуренции? Как учитывается конкуренция в представленных моделях? 7. Какие результаты могут быть получены с помощью модели роста численности популяции с дискретным размножением? 8. Как построить фазовую диаграмму динамики численности популяции с дискретным размножением? 9. Как выводится логистическое уравнение? Каково аналитическое решение этого уравнения? Как в нем учитывается внутривидовая конкуренция? 10. По какому принципу записывается модель межвидовой конкуренции? 11. Какие результаты могут быть получены с помощью модели межвидовой конкуренции? 12. Какие факторы необходимо учесть при разработке модели системы «хищник–жертва»? 13. Какие результаты могут быть получены с помощью модели «хищник–жертва»? 14. Какой вид будет иметь математическая модель межвидовой конкуренции для трех популяций? 15. Как изменится модель «хищник–жертва» есть учесть в ней случайные внешние воздействия, приводящие к изменению численности популяций?
|
||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 415; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.169 (0.013 с.) |

 равна
равна 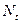 , и изменяется во времени пропорционально величине скорости воспроизводства
, и изменяется во времени пропорционально величине скорости воспроизводства  . Такими видами являются большая часть растений, некоторые виды насекомых. Коэффициент
. Такими видами являются большая часть растений, некоторые виды насекомых. Коэффициент 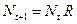 , (3.1)
, (3.1)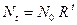 , где
, где 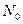 – начальная численность популяции. Эта модель описывает популяцию, в которой отсутствует конкуренция и в которой
– начальная численность популяции. Эта модель описывает популяцию, в которой отсутствует конкуренция и в которой 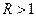 , то численность популяции будет бесконечно увеличиваться. В реальности в какой-то момент начинают работать механизмы сдерживания роста популяции. Следовательно, необходимо изменить уравнение (3.1) таким образом, чтобы чистая скорость воспроизводства зависела от внутривидовой конкуренции.
, то численность популяции будет бесконечно увеличиваться. В реальности в какой-то момент начинают работать механизмы сдерживания роста популяции. Следовательно, необходимо изменить уравнение (3.1) таким образом, чтобы чистая скорость воспроизводства зависела от внутривидовой конкуренции.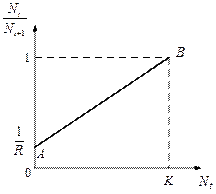
 отражает ситуацию, в которой численность популяции близка к нулю, конкуренция при этом практически отсутствует, и фактическую скорость воспроизводства вполне можно описывать параметром
отражает ситуацию, в которой численность популяции близка к нулю, конкуренция при этом практически отсутствует, и фактическую скорость воспроизводства вполне можно описывать параметром 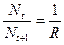 .
. отражает ситуацию, в которой численность популяции высока, и в значительной степени проявляется внутривидовая конкуренция. Фактическая скорость воспроизводства в результате конкуренции настолько снижена, что популяция в целом может не более чем восстанавливать в каждом поколении свою численность, потому что количество родившихся особей уравновешивается количеством погибших. Гипотезе, отраженной на рис. 3.1, соответствует уравнение
отражает ситуацию, в которой численность популяции высока, и в значительной степени проявляется внутривидовая конкуренция. Фактическая скорость воспроизводства в результате конкуренции настолько снижена, что популяция в целом может не более чем восстанавливать в каждом поколении свою численность, потому что количество родившихся особей уравновешивается количеством погибших. Гипотезе, отраженной на рис. 3.1, соответствует уравнение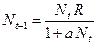 , (3.2)
, (3.2)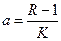 . Это уравнение представляет собой модель роста популяции, ограниченного внутривидовой конкуренцией. Суть этой модели в том, что константа
. Это уравнение представляет собой модель роста популяции, ограниченного внутривидовой конкуренцией. Суть этой модели в том, что константа 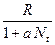 , которая уменьшается по мере роста численности популяции
, которая уменьшается по мере роста численности популяции 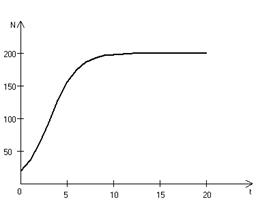
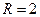 ,
, 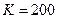 ,
, 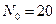
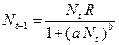 . (3.3)
. (3.3) , который определяет тип зависимости падения скорости роста популяции от ее численности. Набор величин
, который определяет тип зависимости падения скорости роста популяции от ее численности. Набор величин  ,
, 
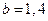 ,
, 
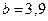 ,
, 
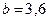 ,
, 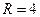
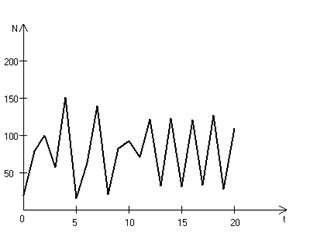
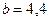 ,
, 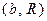 границ, которые разделяют монотонное затухание, затухающие колебания, устойчивые предельные циклы и случайные (хаотические) изменения, рис. 3.4.
границ, которые разделяют монотонное затухание, затухающие колебания, устойчивые предельные циклы и случайные (хаотические) изменения, рис. 3.4.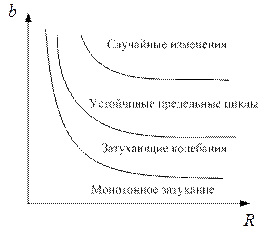
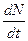 , средняя скорость увеличения численности в расчете на одну особь определяется величиной
, средняя скорость увеличения численности в расчете на одну особь определяется величиной 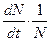 .
.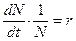 или
или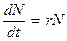 , (3.4)
, (3.4)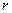 мгновенная удельная скорость роста численности, т.е. приращение численности за единицу времени в пересчете на одну особь. Согласно этой модели, вследствие того, что не учтена внутривидовая конкуренция, численность популяции при
мгновенная удельная скорость роста численности, т.е. приращение численности за единицу времени в пересчете на одну особь. Согласно этой модели, вследствие того, что не учтена внутривидовая конкуренция, численность популяции при 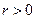 будет неограниченно возрастать, т.е. будет наблюдаться экспоненциальный рост.
будет неограниченно возрастать, т.е. будет наблюдаться экспоненциальный рост.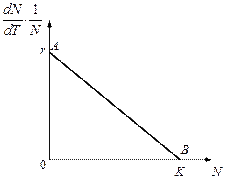
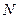 достигается значение
достигается значение 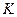 (предельная плотность насыщения), скорость роста популяции снижается до нуля (точка
(предельная плотность насыщения), скорость роста популяции снижается до нуля (точка 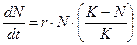 . (3.5)
. (3.5)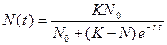 . (3.6)
. (3.6)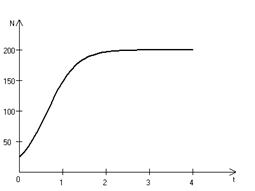
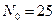 ,
, 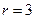
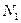 ,
, 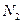 – численность первой и второй популяций,
– численность первой и второй популяций, 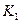 ,
, 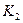 – предельные плотности насыщения,
– предельные плотности насыщения, 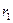 ,
, 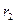 максимальные врожденные скорости роста популяций.
максимальные врожденные скорости роста популяций. особей вида 2 оказывают такое же воздействие на вид 1, как одна особь вида 1. Константу
особей вида 2 оказывают такое же воздействие на вид 1, как одна особь вида 1. Константу 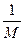 в этом случае называют коэффициентом конкуренции. Обозначим её
в этом случае называют коэффициентом конкуренции. Обозначим её 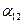 . Таким образом, чтобы отразить суммарное воздействие на вид 1, надо в логистическом уравнении в числителе дроби вместо
. Таким образом, чтобы отразить суммарное воздействие на вид 1, надо в логистическом уравнении в числителе дроби вместо 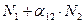 . Аналогично получается уравнение для исследования численности второй популяции. В результате получаем систему двух дифференциальных уравнений:
. Аналогично получается уравнение для исследования численности второй популяции. В результате получаем систему двух дифференциальных уравнений: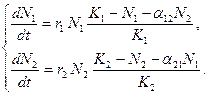 (3.7)
(3.7)
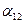 или
или 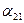 больше единицы, то влияние со стороны конкурирующей популяции на особей данного вида сильнее, чем со стороны особей своего вида.
больше единицы, то влияние со стороны конкурирующей популяции на особей данного вида сильнее, чем со стороны особей своего вида.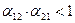 . Сплошная линия – численность первой популяции, штриховая – второй.
. Сплошная линия – численность первой популяции, штриховая – второй.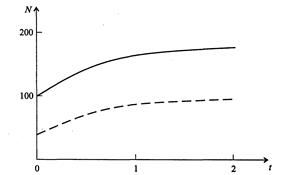
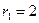 ,
, 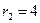 ,
, 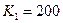 ,
, 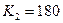 ,
, 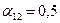 ,
, 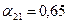 ,
, 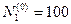 ,
, 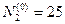
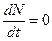 . Из первого уравнения системы (3.7) получаем
. Из первого уравнения системы (3.7) получаем 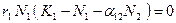 . Равенство выполняется, если один из множителей равен нулю:
. Равенство выполняется, если один из множителей равен нулю: 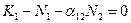 или
или 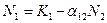 .
.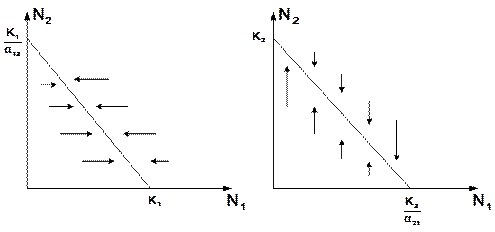
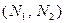 . Вверх и вправо от изоклины из-за высокой численности обеих популяций численность вида 1 снижается, в противоположных направлениях – повышается. Аналогично можно построить изоклину для вида 2. На рис. 3.9 построены соответствующие изоклины, и покачано изменение численности популяций.
. Вверх и вправо от изоклины из-за высокой численности обеих популяций численность вида 1 снижается, в противоположных направлениях – повышается. Аналогично можно построить изоклину для вида 2. На рис. 3.9 построены соответствующие изоклины, и покачано изменение численности популяций.
 – численность популяции хищника,
– численность популяции хищника, 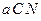 , и окончательно для численности жертвы получаем уравнение
, и окончательно для численности жертвы получаем уравнение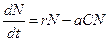 .
.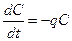 , (
, ( – смертность). Скорость рождения новых особей в данной модели зависит от двух обстоятельств: скорости потребления пищи
– смертность). Скорость рождения новых особей в данной модели зависит от двух обстоятельств: скорости потребления пищи 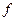 , с которой эта пища переходит в потомство хищника. Итак, для численности хищника окончательно получаем
, с которой эта пища переходит в потомство хищника. Итак, для численности хищника окончательно получаем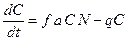 .
.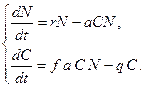 (3.8)
(3.8)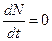 ,
, 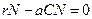 , или выражая
, или выражая 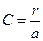 .
.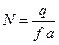 .
.
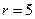 ,
, 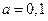 ,
, 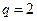 ,
, 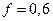 ,
, 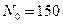 ,
, 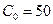 . Сплошная линия численность жертвы, штриховая – хищника.
. Сплошная линия численность жертвы, штриховая – хищника.