
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи для лабораторных работ по темам моделированиеСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Физических процессов и моделирование в экологии
Общие рекомендации 1. Целесообразно применять при моделировании стандартные методы интегрирования систем дифференциальных уравнений: Эйлера, Эйлера – Коши, Рунге – Кутта. 2. Результаты моделирования следует выводить на экран компьютера в виде а) таблиц зависимостей перемещения и скорости от времени, численности популяций от времени; б) графиков зависимостей перемещения и скорости от времени, численности популяций от времени; в) траекторий. Необходимы динамические иллюстрации движения тел (например, изображение движений по траекториям в некотором условном масштабе времени через равные промежутки). Уместны звуковые сигналы (одни – в критические моменты для моделируемого процесса, другие через заданный отрезок пройденного пути или через определенный интервал времени). 3. При выводе результатов в табличном виде следует учитывать, что соответствующий шаг по времени не имеет практически ничего общего с шагом интегрирования и определяется удобством и достаточной полнотой для восприятия результатов на экране. Экран, полностью заполненный числами, зрительно плохо воспринимается, поэтому выводимые числа следует форматировать так, чтобы незначащие цифры практически отсутствовали. 4. При выводе результатов в графической форме графики должны быть построены с указанием величин отложенных по осям, их размерности и масштаба. 5. Поскольку таблицы, графики и траектории на одном экране обычно не помещаются, удобно сделать меню, в котором пользователь выбирает желаемый в настоящий момент вид представления результатов. Задача 1 Изучить, как связана высота прыжка с площадью поперечного сечения парашюта, чтобы скорость приземления была безопасной (не больше Задача 2 Промоделировать падение тела с заданными характеристиками (массой, формой) в различных вязких средах. Изучить влияние вязкости среды на характер движения. Скорость движения должна быть столь невелика, чтобы квадрата составляющей силы сопротивления можно было пренебрегать. Задача 3 Промоделировать падение тела с заданными характеристиками (массой, формой), в различных плотных средах. Изучить влияние плотности среды на характер движения. Скорость движения должна быть достаточно большой, чтобы линейной составляющей силы сопротивления можно было пренебрегать (на большей части пути).
Задача 4 Промоделировать движение исследовательского зонда, «выстреленного» вертикально вверх с уровня земли. В верхней точке траектории над зондом раскрывается парашют, и он плавно спускается в точку старта. Задача 5 Глубинная бомба, установленная на взрыв через заданное время, сбрасывается со стоящего неподвижно противолодочного корабля. Исследовать связь между глубиной, на которой произойдет взрыв, и формой корпуса (сферической, полусферический, каплевидной). Задача 6 Глубинная бомба, установленная на взрыв на заданной глубине, сбрасывается со стоящего неподвижно противолодочного корабля. Исследовать связь между временем достижения заданной глубины и формой корпуса (сферической, полусферической, каплевидной). Задача 7 Провести исследование соотношения входных параметров Задача 8 Разработать и исследовать усовершенствованную модель взлета ракеты, приняв во внимание, что реальные космические ракеты обычно двух- и трехступенчатые и двигатели разных ступеней имеют разную силу тяги. Задача 9 Промоделировать движение исследовательского зонда, снабженного разгонным двигателем небольшой мощности, «выстреленного» вертикально вверх с уровня земли. В верхней точке траектории двигатель выключается, над зондом раскрывается парашют, и он плавно спускается в точку старта. Задача 10 Глубинная бомба-торпеда, снабженная разгонным двигателем, установленная на взрыв через заданное время, сбрасывается со стоящего неподвижно противолодочного корабля. Исследовать связь между глубиной, на которой произойдет взрыв, и формой корпуса (сферической, полусферической, каплевидной). Задача 11 Глубинная бомба-торпеда, снабженная разгонным двигателем, установленная на взрыв на заданной глубине, сбрасывается со стоящего неподвижно противолодочного корабля. Исследовать связь между временем достижения заданной глубины и формой корпуса (сферической, полусферической, каплевидной).
Задача 12 Торпеда, снабженная разгонным двигателем, нацеливается с подводной лодки на стоящий вертикально над ней надводный корабль. Исследовать связь между временем поражения цели и формой корпуса (сферической, полусферической, каплевидной). Задача 13 Построить траектории и найти временные зависимости горизонтальной и вертикальной составляющих скорости и перемещения для тела массой 1 кг, брошенного под углом 45 градусов к горизонту с начальной скоростью 10 м/с: 1) в воздухе; 2) в воде. Сравнить результаты с теми, которые получились бы без учета сопротивления среды (последние можно получить либо численно из той же модели, либо аналитически). Задача 14 Найти вид зависимости горизонтальной длины полета тела и максимальной высоты траектории от одного из коэффициентов сопротивления среды, фиксировав все остальные параметры. Представить эту зависимость графически. Задача 15 Разработать модель подводной охоты. На расстоянии Задача 16 Изучить характер эволюции популяции, описываемый моделью (3.3), при значении параметров Задача 17 Изучить характер эволюции популяции, описываемый моделью (3.3), при значении параметров Задача 18 Изучить характер эволюции популяции, описываемый моделью (3.3), при значении параметров Задача 19 Для модели (3.3) в фазовой плоскости Задача 20 Для модели (3.3) в фазовой плоскости Задача 21 Реализовать моделирование межвидовой конкуренции поформуле (3.7) при значениях параметров Задача 22 Реализовать моделирование межвидовой конкуренции поформуле (3.7) при значениях параметров Задача 23 Построить в фазовой плоскости Задача 24 Провести моделирование динамики численности популяций в системе «хищник — жертва» (модель (3.8)) при значениях параметров
Задача 25 Провести моделирование динамики численности популяций в системе «хищник — жертва» (модель (3.8)) при значениях параметров Задача 26 Провести моделирование динамики численности популяций в системе «хищник — жертва» (модель (3.8)) при значениях параметров Задача 27 Провести моделирование динамики численности популяций в системе «хищник — жертва» (модель (3.8)) при значениях параметров Задача 28 Провести моделирование динамики численности популяций в системе «хищник — жертва» (модель (3.8)) при значениях параметров Задача 29 Модель (3.8) предсказывает сопряженные колебания численности жертв и хищников. Исследовать зависимость запаздывания амплитуд колебаний численности хищников от амплитуд колебаний численности жертв в зависимости от значений параметра Задача 30 Модель (3.8) предсказывает сопряженные колебания численности жертв и хищников. Исследовать зависимость запаздывания амплитуд колебаний численности хищников от амплитуд колебаний численности жертв в зависимости от соотношения значений начальных численностей популяций
Приложение 3
Тестовые задания
Вариант №1
1. Цели моделирования определяются на этапе …. Варианты ответов: а) разработки математической модели; б) разработки концептуальной модели; в) разработки имитационной модели; г) постановки задачи.
2. Процесс описания объекта на искусственном языке называют … объекта. Варианты ответов: а) компиляцией; б) семантическим анализом; в) формализацией; г) синтаксическим анализом.
3. К моделированию нецелесообразно прибегать, когда…. Варианты ответов: а) создание объекта чрезвычайно дорого; б) не определены существенные свойства исследуемого объекта; в) исследование самого объекта приводит к его разрушению; г) процесс очень медленный.
4. Модель может быть построения для любого …. Варианты ответов:
а) объекта явления или процесса; б) только объекта или процесса; в) только объекта или явления; г) только объекта.
5. Примером неформализованного описания модели служит …. Варианты ответов: а) фотография объекта; б) инструкция пилота самолета; в) запись алгоритма в виде блок-схемы; г) уравнение 3-го закона Ньютона.
6. Верное соответствие для представленной таблицы моделирования
имеет вид: Варианты ответов: а) 1C 2D 3B 4A; б) 1D 2A 3B 4C; в) 1D 2C 3A 4B; г) 1C 2A 3B 4D.
7. Компьютерным моделированием называется …. Варианты ответов: а) процесс построения модели компьютерными средствами; б) построение модели на экране компьютера; в) процесс исследования объекта с помощью его компьютерной модели; г) решение конкретной задачи с помощью компьютера.
8. Математической моделью является …. Варианты ответов: а) модель автомобиля; б) сборник правил дорожного движения; в) номенклатура списка товаров на складе; г) формула закона всемирного тяготения.
9. Стохастической моделью является …. Варианты ответов: а) модель движения тела, брошенного под углом к горизонту; б) модель броуновского движения; в) модель таяния кусочка льда в стакане; г) модель обтекания газом крыла самолета.
10. Последовательность этапов моделирования имеет вид: Варианты ответов: а) объект, цель, модель, эксперимент, программа, анализ, тестирование; б) цель, модель, объект, алгоритм, программа, эксперимент, уточнение выбора объекта; в) цель, объект, модель, метод, алгоритм, программа, эксперимент, анализ, уточнение; г) объект, модель, цель, алгоритм, метод, программа, эксперимент.
11. Система дифференциальных уравнений, описывающая свободное падение тела с учетом сопротивления среды имеет вид: Варианты ответов: а) б) в) г)
12. Сила сопротивления зависит от …. Варианты ответов: а) размеров тела и плотности среды; б) формы тела и температуры среды; в) направления движения и массы тела; г) скорости и плотности тела.
13. Скорость ракеты при взлете определяется из уравнения …. Варианты ответов: а) б) в) г)
14. Первая космическая скорость равна …. Варианты ответов: а) б) в) г)
15. Максимальная высота подъема тела, брошенного под углом Варианты ответов: а) б) в) г)
16. Траектория движения тела, брошенного под углом Варианты ответов: а) б) в) г)
17. Вертикальная составляющая скорости тела, брошенного под углом
Варианты ответов: а) б) в) г)
18. Аналитическая запись третьего закона Кеплера имеет вид: Варианты ответов: а) б) в) г)
19. Количества тепла, проходящее через поперечное сечение стержня в точке Варианты ответов: а) б) в) г) 20. Уравнение теплопроводности в трехмерном случае имеет вид: Варианты ответов: а) б) в) г)
21. Дискретная модель численности популяций, зависящей от чистой скорости воспроизводства (без учета внутривидовой конкуренции, Варианты ответов: а) б) в) г)
22. Непрерывная модель численности популяций, с учетом внутривидовой конкуренции ( Варианты ответов: а) б) в) г)
23. Модель межвидовой конкуренции для случая двух популяций с численностью Варианты ответов: а) б) в) г)
24. Модель межвидовой конкуренции «хищник-жертва» ( Варианты ответов: а) б) в) г)
25. Численность популяции хищников в модели межвидовой конкуренции «хищник-жертва» ( Варианты ответов: а) б) в) г)
26. Коэффициенты прямых материальных затрат определяются по формуле: Варианты ответов: а) б) в) г)
27. Объем конечной продукции каждой отрасли Варианты ответов: а) б) в) г)
28. Матрица Варианты ответов: а) б) в) г)
29. Коэффициент прямой фондоемкости продукции Варианты ответов: а) б) в) г)
30. Матрица прямых материальных затрат Варианты ответов: а) наибольшее по модулю собственное значение б) все главные миноры матрицы в) норма матрицы г) матрица
Ответы
Вариант №2
1. Результатом процесса формализации является …. Варианты ответов: а) математическая модель; б) описательная модель; в) материальная модель; г) вербальная модель.
2. Расположите этапы моделирования в правильной последовательности: А) Синтез математической модели области, выбор критериев оценки эффективности и точности моделирования. Б) Разработка имитационной модели, алгоритма ее реализации. В) Анализ моделируемой системы, сбор необходимой информации, выделение проблемной области исследования и постановка задачи. Г) Анализ результатов моделирования. Д) Оценка адекватности имитационной модели. Варианты ответов: а) В, А, Б, Г, Д; б) Б, В, А, Г, Д; в) В, А, Б, Д, Г; г) В, Б, А, Д, Г.
3. Верное соответствие для представленной таблицы моделирования
имеет вид: Варианты ответов: а) 1D 2A 3C 4B; б) 1D 2C 3A 4B; в) 1C 2D 3B 4A; г) 1C 2A 3B 4D.
4. Среди общепринятых классификаций видов моделей отсутствует их деление на …. Варианты ответов: а) детерминированные – стохастические; б) логические – сенсорные; в) статические – динамические; г) дискретные – непрерывные.
5. Модель гравитационного взаимодействия двух тел, записанная в виде формул, является …. Варианты ответов: а) описательной информационной моделью; б) формальной математической моделью; в) экспериментальной предметной моделью; г) формальной логической моделью.
6. Моделью называется …. Варианты ответов: а) образ оригинала с наиболее присущими ему свойствами; б) оригинал в миниатюре; в) точная копия оригинала; г) начальный замысел будущего объекта.
7. Детерминированной моделью является …. Варианты ответов: а) модель свободного падения тела в среде с сопротивлением; б) модель формирования очереди; в) модель случайного блуждания частицы; г) модель игры «орел-решка».
8. Компьютерным экспериментом называется …. Варианты ответов: а) решение задачи на компьютере; б) автоматизированное управление физическим экспериментом; в) подключение компьютера для обработки физических экспериментов; г) исследование модели с помощью компьютерной программы.
9. Если полученные результаты моделирования не соответствуют ожидаемым, то необходимо …. Варианты ответов: а) изменение метода исследования; б) изменить алгоритм программной реализации; в) провести повторный анализ результатов; г) уточнение модели.
10. Адекватность модели реальному процессу устанавливается после …. Варианты ответов: а) построения математической модели; б) отладки и тестирования программы; в) выполнения численного эксперимента; г) выбора метода исследования.
11. Свободное падение тела описывается системой дифференциальных уравнений Варианты ответов: а) б) в) г)
12. Сила сопротивления …. Варианты ответов: а) прямопропорциональна скорости тела; б) не зависит от скорости тела; в) обратнопропорциональна скорости тела; г) равна произведению массы тела на его скорость.
13. Сила сопротивления действующая на ракету при взлете равна…. Варианты ответов: а) б) в) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 ).
). и
и  ,при которых ракета достигнет первой космической скорости (и в соответствующий момент исчерпает горючее). Остальные входные параметры фиксировать произвольно. Построить соответствующую фазовую диаграмму в переменных (
,при которых ракета достигнет первой космической скорости (и в соответствующий момент исчерпает горючее). Остальные входные параметры фиксировать произвольно. Построить соответствующую фазовую диаграмму в переменных (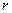 под углом
под углом  подводный охотник видит неподвижную акулу. На сколько метров выше нее надо целиться, чтобы гарпун попал в цель?
подводный охотник видит неподвижную акулу. На сколько метров выше нее надо целиться, чтобы гарпун попал в цель? ,
, 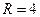 ,
,  в зависимости от значения параметра
в зависимости от значения параметра  в диапазоне
в диапазоне  . Есть ли качественные различия в характере эволюции в зависимости от значения
. Есть ли качественные различия в характере эволюции в зависимости от значения 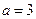 ,
,  ,
,  в диапазоне
в диапазоне  . Есть ли качественные различия в характере эволюции в зависимости от значения
. Есть ли качественные различия в характере эволюции в зависимости от значения  ,
,  в диапазоне
в диапазоне  . Есть ли качественные различия в характере эволюции в зависимости от значения
. Есть ли качественные различия в характере эволюции в зависимости от значения 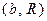 найти границы зон, разделяющих режимы монотонного и колебательного установления стационарной численности популяции изучаемой системы.
найти границы зон, разделяющих режимы монотонного и колебательного установления стационарной численности популяции изучаемой системы. ,
,  ,
,  ,
,  ,
,  ,
,  . Проанализировать зависимость судьбы популяций от соотношения значений их начальной численности
. Проанализировать зависимость судьбы популяций от соотношения значений их начальной численности  ,
,  .
. ,
,  . Проанализировать зависимость судьбы популяций от соотношения значений коэффициентов конкуренции
. Проанализировать зависимость судьбы популяций от соотношения значений коэффициентов конкуренции  ,
, 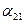 .
. границы зон, разделяющих какие-либо два режима эволюции конкурирующих популяций (в соответствии с моделью (3.7)). Остальные параметры модели выбрать произвольно. Учесть, что режим устойчивого сосуществования популяций может реализоватьсятолько при
границы зон, разделяющих какие-либо два режима эволюции конкурирующих популяций (в соответствии с моделью (3.7)). Остальные параметры модели выбрать произвольно. Учесть, что режим устойчивого сосуществования популяций может реализоватьсятолько при 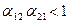 .
.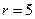 ,
, 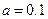 ,
, 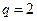 ,
, 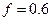 . Проанализировать зависимость исхода эволюции от соотношения значений параметров
. Проанализировать зависимость исхода эволюции от соотношения значений параметров 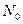 и
и  .
. . Проанализировать зависимость результатов моделирования от значения параметра
. Проанализировать зависимость результатов моделирования от значения параметра 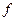 в диапазоне
в диапазоне  .
. ,
,  в диапазоне
в диапазоне  .
. .
. .
. ,
,  -масса,
-масса,  -скорость,
-скорость,  -высота,
-высота, 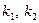 -коэффициенты;
-коэффициенты; ,
, 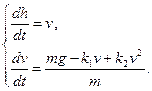 ,
,  ,
,  ;
;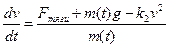 ;
; ;
; .
. ;
; ;
; ;
; .
. , без учета силы сопротивления равна ….
, без учета силы сопротивления равна …. ;
; ;
; ;
;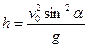 .
. ;
; ;
; ;
; .
. ;
; ;
; ;
; .
. ;
; ;
; ;
;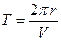 .
. , за время
, за время  определяется по формуле:
определяется по формуле: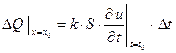 ;
; ;
; ;
; .
. ;
;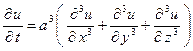 ;
; ;
; .
.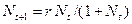 ;
;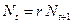 ;
; ;
; .
.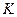 -предельная плотность насыщения) имеет вид:
-предельная плотность насыщения) имеет вид: ;
;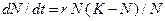 ;
; ;
; .
.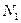 ,
,  (
(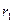 ,
, 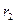 -врожденные скорости роста популяций,
-врожденные скорости роста популяций, 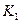 ,
, 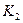 -предельные плотности насыщения,
-предельные плотности насыщения,  ,
, 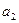 коэффициенты конкуренции) имеет вид:
коэффициенты конкуренции) имеет вид: ,
,  ;
; ,
,  ;
; ,
,  ;
;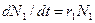 ,
,  .
. -численность, скорость роста, коэффициент эффективности поиска,
-численность, скорость роста, коэффициент эффективности поиска,  -численность, эффективность добычи, коэффициент смертности популяции хищника) имеет вид:
-численность, эффективность добычи, коэффициент смертности популяции хищника) имеет вид: ,
,  ;
; ;
; ,
, 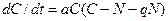 ;
;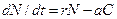 ,
,  .
.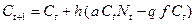 ;
; ;
;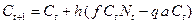 ;
;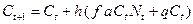 .
.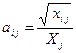 ,
,  ,
,  – величина межотраслевых потоков продукции,
– величина межотраслевых потоков продукции,  – величина валового продукта;
– величина валового продукта; ,
, 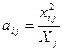 ,
,  ,
,  определяется по формуле:
определяется по формуле: ,
, 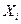 – величина валовой продукции каждой отрасли,
– величина валовой продукции каждой отрасли,  – матрица коэффициентов прямых материальных затрат;
– матрица коэффициентов прямых материальных затрат; ,
,  ,
,  ,
,  , такой что выполняется неравенство:
, такой что выполняется неравенство: ;
; ;
; ;
; .
.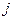 отрасли определяется по формуле:
отрасли определяется по формуле: ,
,  – величина валовой продукции каждой отрасли,
– величина валовой продукции каждой отрасли,  – объемы производственных фондов, занятые в
– объемы производственных фондов, занятые в  ,
,  ,
,  ,
,  матрицы
матрицы 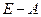 положительны;
положительны; ;
;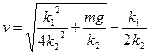 ;
;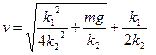 ;
;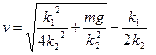 .
.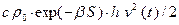 ,
,  – коэффициент лобового сопротивления,
– коэффициент лобового сопротивления,  – площадь поперечного сечения,
– площадь поперечного сечения,  – плотность около поверхности земли;
– плотность около поверхности земли; ,
,  ,
, 


