
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 5. Математические модели в медицине и биологииСодержание книги Поиск на нашем сайте
5.1. Математическая модель лазер-индуцированного тромбообразования в микрососудах живых организмов. Рассматривается математическая модель явления, в котором на равных выступают физические и биологические факторы, определяющие характер происходящих процессов. Исследуется индуцированный лазерным излучением феномен тромбообразования в кровеносных микрососудах живых организмов. Искусственно индуцированный рост тромба начинается, когда стенка кровеносного сосуда обжигается сфокусированным на ней лазерным излучением. Из пораженного участка внутренней поверхности кровеносного сосуда начинается выделение аденозиндифосфорной кислоты (АДФ), которое приводит к активизации тромбоцитов в потоке крови, служащих строительным материалом при формировании тромба [10-13]. Для образования тромба стенка сосуда повреждается излучением импульсного азотного лазера с длиной волны Процесс тромбообразования протекает в три стадии: 1. Начальная стадия – образование тромба в результате какого-либо повреждения стенки сосуда. 2. Агрегационная стадия характеризуется ростом тромба и определяется как физиологическими особенностями взаимодействия тромбоцитов с растущим тромбом, так и гидродинамическими характеристикам кровотока. 3. Заключительная стадия, на которой рост тромба заканчивается, определяется резко изменившимися условиями протекания крови, к которым приводит частичная закупорка кровеносного сосуда. Математическая модель, описывающая агрегационную и заключительную стадии, строится на основе имеющихся экспериментальных данных и разумных соображений и предположений. Выбор приемлемого уровня сокращенного описания процесса позволяет резко сократить число вводимых феноменологических параметров и развить достаточно простую модель явления, передающую все его характерные наблюдаемые «макроскопические» черты. Реология крови устанавливает следующий закон изменения гидродинамической скорости крови вдоль поперечного сечения сосуда:
где
где
Из соотношений (5.2), (5.3) следует, что выражение для скорости
где С другой стороны, зависимость скорости кровотока в сосуде (5.1) совместно с соображениями размерности приводит к следующему выражению скорости
Сравнение выражений (5.4) и (5.5) показывает, что скорость
Соотношение (5.6) позволяет записать уравнение непрерывности в терминах скорости на оси сосуда:
где Из уравнения (5.2) следует, что сужение пропускного отверстия сосуда в результате роста тромба сопровождается увеличением разностидавлений в поперечных сечениях, отстоящих друг от друга на расстоянии
Когда разность давлений С учетом того, что
где Введя параметр
Смысл и численное значение параметра На рис. 5.1 сплошной линией представлена экспериментально полученная усредненная кривая зависимости скорости кровотока от размера тромба. Пунктиром покачана кривая, соответствующая уравнению непрерывности.
Рис. 5.1. Зависимость скорости кровотока от размера тромба Уравнение (5.10) в точности описывает левую часть экспериментальной кривой. Чтобы правильно описать поведение всей этой кривой, введем функцию
в которой На основании (5.11) выражение для скорости кровотока примет вид:
Из формулы (5.11) следует, что при малых размерах тромба, когда Измерения зависимости скорости роста тромба
Рис. 5.2. Зависимость скорости роста тромба от скорости кровотока Значение скорости кровотока, при которой достигается максимум скорости роста тромба, и максимальное значение этой скорости зависят от диаметра кровеносных сосудов, но во всех случаях кривая имеет такой характерный вид. Анализ показал, что даже простейшая интерполяция экспериментальной кривой на рис. 5.2 оказывается достаточной для определения размера тромба
где
а при больших значениях скорости, когда
Введя два новых параметра
где функция
Уравнение (5.16) совместно с (5.11) и (5.15) завершает построение математической модели рассматриваемого явления. Модель содержит четыре феноменологических параметра
Решение определяет закон роста тромба со временем. 5.2. Исследование модели лазер-индуцированного тромбообразования. Описанная модель лазер-индуцированного тромбообразования основывается на двух моделях, описывающих экспериментальные результаты изучения зависимости скорости кровотока в сосуде от размеров растущего тромба и зависимости скорости роста тромба от скорости крови в сосуде. Первая из этих моделей основывается на физическом законе течения жидкости – уравнении непрерывности, модифицированном для возможности учета на феноменологическом уровне физиологического явления компенсации, проявляющегося в живом организме в условиях роста градиента давления крови в потоке. Вторая модель не имеет под собой столь надежной теоретической базы и основана на анализе экспериментальной картины поведения тромбоцитов в условиях прохождения мимо поврежденного участка стенки сосуда. Простота модели позволяет провести аналитическое исследование и частичное определение области возможных значений феноменологических параметров. Начнем с анализа свойств функций На начальной стадии роста тромба скорость течения крови в сосуде всегда увеличивается вследствие уменьшения площади поперечного сечения сосуда. Это условие приводит к неравенству Таким образом, область возможных значений отношения
Функция
при значении
Таким образом, максимальное значение Экстремумы функции
Решение (5.20) тождественно решению двух следующих уравнений:
Решение уравнения (5.21) соответствует максимуму функции 1. Если значения феноменологического параметра
где максимальное значение
Рис. 5.3. Иллюстрация зависимости 2. Если значения параметра
то функция
Рис. 5.4. Иллюстрация зависимости 3. Если значения параметра
Рис. 5.5. Иллюстрация зависимости Графики функций В самом начале образования тромба ( Значение параметра Численный анализ показывает, что параметр Выясним смысл и возможные значения остальных трех параметров. Выше уже была найдена область возможных значений отношения Параметр Параметр Представленную модель можно улучшить, учитывая большое число факторов, влияющих на рост тромба и используя лучшую аппроксимацию для экспериментальной зависимости скорости роста тромба Программа, численно моделирующая скорость роста тромба имеет вид: program tromb; uses crt,graph; const eps=1; gamma=2.5; alfa=10; beta=0.9; dt=0.01; u1=40; u2=340; v1=40; v2=340; var m,t,fi,psi,max_m,max_fi,max_psi:extended; k,u_t,u1_t,v_fi,v1_fi,v_psi,v1_psi,v_m,v1_m,tmax,max:integer; x_1,x_2,y_1,y_2,x,y:integer; kt,km,kfi,kpsi:extended; adapter,regim,i:integer; str_1:string; function ffi(m:extended):extended; begin ffi:=exp(-eps*m)/(1-(gamma*m*exp(-eps*m))); end; function fpsi(m:extended):extended; begin fpsi:=alfa*ffi(m)*exp(-beta*ffi(m)); end; begin clrscr; adapter:=detect; inigraph(adapter,regim,'d:\lang\bp\bgi'); t:=0; m:=0; tmax:=10; max_m:=0; max_fi:=0; max_psi:=0; repeat t:=t+dt; fi:=ffi(m); psi:=fpsi(m); m:=m+dt*fpsi(m); if fi>max_fi then max_fi:=fi; if psi>max_psi then max_psi:=psi; if m>max_m then max_m:=m; until t>=tmax; if (max_m>max_fi) and (max_m>max_psi) then max:=round(max_m); if (max_fi>max_m) and (max_fi>max_psi) then max:=round(max_fi); if (max_psi>max_m) and (max_psi>max_fi) then max:=round(max_psi); if tmax mod 10<>0 then tmax:=round(tmax)+(10-(round(tmax) mod 10)); if max mod 10<>0 then max:=round(max)+(10-(round(max) mod 10)); kt:=10*(u2-u1)/(11*tmax); km:=10*(v2-v1)/(11*max); kfi:=10*(v2-v1)/(11*max); kpsi:=10*(v2-v1)/(11*max); setcolor(white); line(u1,v2,u2,v2); line(u1,v2,u1,v1); line(u2,v2,u2-10,v2+5); line(u2,v2,u2-10,v2-5); line(u1,v1,u1-5,v1+10); line(u1,v1,u1+5,v1+10); outtextxy(u1-5,v2+5,'O'); outtextxy(u1+10,v1,'m,fi,psi'); outtextxy(u2-10,v2-15,'t'); for i:=1 to 10 do begin y:=round(v2-(i*(v2-v1)/11)); x_1:=u1-5; x_2:=u1+5; line(x_1,y,x_2,y); str(i*max/10:3:0,str_1); outtextxy(u1-40,y,str_1); end; for i:=1 to 10 do begin x:=round(u1+(i*(u2-u1)/11)); y_1:=v2-5; y_2:=v2+5; line(x,y_1,x,y_2); str(i*tmax/10:2:0,str_1); outtextxy(x-10,v2+10,str_1); end; t:=0; m:=0; fi:=ffi(m); psi:=fpsi(m); u_t:=round(u1+kt*t); v_m:=round(v2-km*m); v_fi:=round(v2-kfi*fi); v_psi:=round(v2-kpsi*psi); repeat t:=t+dt; fi:=ffi(m); psi:=fpsi(m); m:=m+dt*fpsi(m); k:=k+1; if k=10 then begin u1_t:=round(u1+kt*t); v1_m:=round(v2-km*m); v1_fi:=round(v2-kfi*fi); v1_psi:=round(v2-kpsi*psi); setcolor(4); line(u_t,v_m,u1_t,v1_m); setcolor(1); line(u_t,v_fi,u1_t,v1_fi); setcolor(2); line(u_t,v_psi,u1_t,v1_psi); u_t:=u1_t; v_m:=v1_m; v_fi:=v1_fi; v_psi:=v1_psi; k:=0; end; until (t>=tmax) or keypressed; readln; closegraph; end. 5.3. Модель ростовых пульсаций в биологии. Опыты в эмбриологии свидетельствуют о том, что формирование и развитие живых организмов генетически предопределено. Однако в основе формообразовательных процессов в клеточной массе лежат физические и физико-химические свойства отдельных клеток и их взаимодействия между собой и с окружением. На основе измерений можно получать информацию о феноменологических параметрах, определяющих наблюдаемые явления в клеточных структурах, и проводить надлежащий выбор самих этих параметров [14]. Ниже рассматривается математическая модель роста гидрантов. Внешнее строение объекта представлено на рис. 5.6. Гидрант формируется из боковой почки ветвящегося ствола в результате ее роста. На заключительном этапе происходит формирование головного отдела, главными элементами которого являются гипостом (рот) и щупальца. На рис. 5.6 показана упрощенная схема строения отдельной растущей почки.
Рис. 5.6. Схема строения почки Рост почки протекает немонотонно во времени, продолжается 12-18 часов и сводится в основном к линейному удлинению в продольном направлении. Все стороны функциональной роли ростовых пульсаций остаются пока не выясненными. Несомненно, что они играют решающую роль для питания почки. При ритмических изменениях объема клеток происходит сжатие и растяжение всего эктодермального пласта, в результате чего ритмически изменяется объем и давление в гастральной полости. В результате работы этого насоса почка получает пищу из основного ствола и избавляется от продуктов ее переваривания. Решающим фактором в механизме пульсаций объема клеток являются механические свойства внешней клеточной мембраны и ее модуль упругости
Модуль упругости можно определить либо по наклону зависимости При относительно быстром увеличении объема клетки ее внешняя мембрана оказывается в неравновесном растянутом состоянии и, следовательно, обладает избыточной энергией по отношению к недеформированному состоянию. Среди различных микросостояний, реализующих данное растянутое макроскопическое состояние, есть состояние локального равновесия, при котором энергия будет ниже, чем в любом другом состоянии при данной деформации. При поддержании деформации система придет именно в это состояние локального равновесия, спустя определенное время релаксации При построении модели явления предполагается, что давление зависит не только от объема
Простота уравнения (5.24) соответствует сокращенному описанию процесса на феноменологическом уровне, поскольку в огрубленном временном масштабе не рассматриваются конформационные перестройки и перемещения макромолекулярных компонент мембраны, происходящие в более тонкой временной шкале. На основе экспериментальных данных для
Из соотношения (5.25) следуют формулы
Кроме модуля упругости из данных эксперимента определяется значение гидравлической проводимости мембраны
где Экспериментальная зависимость гидравлической проводимости
Рис. 5.7. Зависимость гидравлической проводимости от давления Осмотический и гидравлический потоки составляют лишь часть всего водного транспорта через мембрану. С учетом проникающих через мембрану растворенных веществ выражение для полного потока
где Такого простейшего приближения достаточно, для того чтобы могли возникнуть клеточные пульсации. Выражение (5.28) определяет скорость изменения объема эктодермальных клеток в соответствии с формулой
На основе эксперимента установлено, что пульсируют только клетки, объединенные в эктодермальный пласт. В почке связывающим элементом в пласте служит базальная мембрана. При изменении объема возникают упругие деформации в базальной мембране. Если все присутствующие в (5.28) факторы (осмотический и гидравлический перепады давления и поток Релаксация объема за счет гидравлической проводимости клеточной стенки идет со скоростью
С учетом соотношений (5.28) – (5.30) можно проследить за эволюцией клеточного объема. Вводя величину
Исследуем систему (5.31) используя фазовую плоскость
При монотонной зависимости
Дифференцируя первое уравнение системы (5.31) получаем, что условие (5.32) эквивалентно следующему уравнению
Зависимость
где
В этом случае L-изоклина имеет две ниспадающие ветви, разделенные растущим участком (рис. 5.8).
Рис. 5.8. Примерный вид нуль-изоклин системы (5.31) Анализ показывает, что общим требованием для возможности существования двух экстремумов является достаточно быстрое убывание гидравлической проводимости с ростом давления (рис. 5.7). При вариации параметров Пока стационарное состояние приходится на падающие участки N-образной изоклины, оно асимптотически устойчиво. Это означает, что в соответствующей области значений параметров исключено возникновение ритмических пульсаций. Поэтому достаточно рассмотреть динамику малых отклонений от стационарной точки:
Линеаризуя систему уравнений (5.31) по величинам
где Показатель
где
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 253; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.115.43 (0.023 с.) |

 нм. Длительность импульсов
нм. Длительность импульсов  с, частота импульсов – 50 Гц, диаметр пучка излучения лазера – 10 нм. Точность измерения скорости кровотока составляет ±10 %.
с, частота импульсов – 50 Гц, диаметр пучка излучения лазера – 10 нм. Точность измерения скорости кровотока составляет ±10 %. , (5.1)
, (5.1)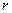 – кратчайшее расстояние от выделенной точки поперечного сечения до стенки сосуда. Объем
– кратчайшее расстояние от выделенной точки поперечного сечения до стенки сосуда. Объем  крови, рассматриваемый как вязкая ньютоновская жидкость с постоянной плотностью, протекающий через поперечное сечение сосуда в единицу времени определяется как
крови, рассматриваемый как вязкая ньютоновская жидкость с постоянной плотностью, протекающий через поперечное сечение сосуда в единицу времени определяется как , (5.2)
, (5.2) – вязкость крови;
– вязкость крови;  –изменение давления крови на расстоянии
–изменение давления крови на расстоянии  вдоль кровеносного сосуда радиуса
вдоль кровеносного сосуда радиуса  . Этот объем можно записать в виде произведения средней скорости
. Этот объем можно записать в виде произведения средней скорости  кровотока по поперечному сечению на площадь поперечного сечения сосуда:
кровотока по поперечному сечению на площадь поперечного сечения сосуда: . (5.3)
. (5.3) , (5.4)
, (5.4) .
. кровотока на оси кровеносного сосуда:
кровотока на оси кровеносного сосуда: . (5.5)
. (5.5) . (5.6)
. (5.6)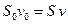 , (5.7)
, (5.7) и
и 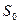 – площади двух различных поперечных сечений сосуда, а
– площади двух различных поперечных сечений сосуда, а  – скорости кровотока на осях этих сечений.
– скорости кровотока на осях этих сечений. . (5.8)
. (5.8) перепишем (5.7) в виде
перепишем (5.7) в виде , (5.9)
, (5.9) – площадь поперечного сечения тромба.
– площадь поперечного сечения тромба. , характеризующий размер тромба, преобразуем равенство (5.9) следующим образом:
, характеризующий размер тромба, преобразуем равенство (5.9) следующим образом: . (5.10)
. (5.10) зависит от выбора и смысла величины
зависит от выбора и смысла величины 
 , (5.11)
, (5.11) и
и  . (5.12)
. (5.12) , функция
, функция  ведет себя как
ведет себя как  , т.е. соответствует уравнению непрерывности. При достаточно больших значениях
, т.е. соответствует уравнению непрерывности. При достаточно больших значениях  от скорости кровотока в сосуде привели к установлению немонотонной зависимости, представленной на рис. 5.2.
от скорости кровотока в сосуде привели к установлению немонотонной зависимости, представленной на рис. 5.2.
 , (5.13)
, (5.13) и
и  некоторые положительные константы. При малых скоростях, когда
некоторые положительные константы. При малых скоростях, когда  , выражение (5.13) соответствует линейной зависимости
, выражение (5.13) соответствует линейной зависимости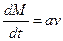 ,
, , выражение (5.13) соответствует экспоненциальному убыванию производной
, выражение (5.13) соответствует экспоненциальному убыванию производной  . (5.14)
. (5.14) и
и  , перепишем уравнение (5.14) в виде
, перепишем уравнение (5.14) в виде , (5.15)
, (5.15) определяется равенством
определяется равенством . (5.16)
. (5.16) ,
, 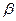 ,
,  .
. ,определяемых выражениями (5.11) и (5.16).
,определяемых выражениями (5.11) и (5.16). . Знаменатель выражения для функции
. Знаменатель выражения для функции  .
. :
: . (5.17)
. (5.17) (5.18)
(5.18) равном
равном . (5.19)
. (5.19) зависит только от величины соотношения
зависит только от величины соотношения  , зависит от двух параметров:
, зависит от двух параметров:  . (5.20)
. (5.20) ; (5.21)
; (5.21) . (5.22)
. (5.22) ,
, определяется выражением (5.18),то функция
определяется выражением (5.18),то функция 
 ,
, определяемой выражением (5.19), и два максимума по обе стороны от минимума, причем правый максимум расположен в области значений
определяемой выражением (5.19), и два максимума по обе стороны от минимума, причем правый максимум расположен в области значений  (рис. 5.4).
(рис. 5.4).
 и еще один максимум справа от
и еще один максимум справа от  (рис. 5.5).
(рис. 5.5).

 ) функция
) функция  и уменьшается с ростом
и уменьшается с ростом  . Если
. Если  ,т.е. скорость течения крови в начале процесса роста тромба соответствует той части на рис. 5.2 предыдущего раздела, где скорость роста тромба увеличивается с ростом скорости кровотока, то
,т.е. скорость течения крови в начале процесса роста тромба соответствует той части на рис. 5.2 предыдущего раздела, где скорость роста тромба увеличивается с ростом скорости кровотока, то  . Если
. Если  ,то аналогичные соображения приводят к выводу, что
,то аналогичные соображения приводят к выводу, что  .
. . Значение этого параметра определяется соотношением между
. Значение этого параметра определяется соотношением между  – значением скорости кровотока, соответствующей максимальному значению скорости роста тромба. Значение
– значением скорости кровотока, соответствующей максимальному значению скорости роста тромба. Значение  на заключительной стадии роста тромба. Значение этого параметра сильно влияет на кривизну и степень убывания функции
на заключительной стадии роста тромба. Значение этого параметра сильно влияет на кривизну и степень убывания функции  после прохождения максимума этой функции. Рост тромба приводит к увеличению аортного или венозного сопротивления. Физиологический компенсационный механизм может регулировать сопротивление, подключая параллельно поврежденному дополнительные кровеносные микрососуды. Это приводит к уменьшению среднего значения скорости крови в сосуде с тромбом. Таким образом, параметр
после прохождения максимума этой функции. Рост тромба приводит к увеличению аортного или венозного сопротивления. Физиологический компенсационный механизм может регулировать сопротивление, подключая параллельно поврежденному дополнительные кровеносные микрососуды. Это приводит к уменьшению среднего значения скорости крови в сосуде с тромбом. Таким образом, параметр 
 . (5.23)
. (5.23) в стационарных условиях эксперимента (
в стационарных условиях эксперимента ( ), либо по приросту
), либо по приросту  , не дожидаясь установления стационарного состояния (
, не дожидаясь установления стационарного состояния ( ). Измеренные значения
). Измеренные значения  . Если время проведения измерения окажется больше времени релаксации, то в эксперименте зафиксируется меньшее значение модуля упругости, чем при быстром изменении объема.
. Если время проведения измерения окажется больше времени релаксации, то в эксперименте зафиксируется меньшее значение модуля упругости, чем при быстром изменении объема. , определяемого по формуле:
, определяемого по формуле: . (5.24)
. (5.24) . Из (5.23), (5.24) получаем
. Из (5.23), (5.24) получаем . (5.25)
. (5.25) ,
,  . (5.26)
. (5.26) . В отсутствие проникающих через мембрану растворенных веществ объемный поток воды определяется гидростатическим
. В отсутствие проникающих через мембрану растворенных веществ объемный поток воды определяется гидростатическим  перепадами давления:
перепадами давления: ,
, – поток воды из клетки;
– поток воды из клетки;  ,
,  .
.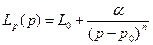 . (5.27)
. (5.27)
 , (5.28)
, (5.28) – постоянный поток, связанный с растворенными веществами.
– постоянный поток, связанный с растворенными веществами. . (5.29)
. (5.29) , где
, где  – феноменологический параметр, имеющий смысл модуля упругости.
– феноменологический параметр, имеющий смысл модуля упругости. . (5.30)
. (5.30) , получим систему, моделирующую ростовые пульсации в биологии
, получим систему, моделирующую ростовые пульсации в биологии (5.31)
(5.31) . Характер поведения возможных фазовых траекторий определяется видом нуль-изоклин:
. Характер поведения возможных фазовых траекторий определяется видом нуль-изоклин: ,
,  .
. возникновение устойчивых колебаний параметров
возникновение устойчивых колебаний параметров  , определяемая уравнением
, определяемая уравнением  , имеет два экстремума – минимум и максимум, т.е. выполняются условия
, имеет два экстремума – минимум и максимум, т.е. выполняются условия ,
,  . (5.32)
. (5.32) . (5.33)
. (5.33) не имеет особенностей. Так как амплитуда пульсаций
не имеет особенностей. Так как амплитуда пульсаций  в первом приближении можно считать постоянной величиной –
в первом приближении можно считать постоянной величиной –  . Пренебрегать зависимостью
. Пренебрегать зависимостью  , (5.34)
, (5.34) , должно иметь два вещественных корня. Если рассмотреть условие
, должно иметь два вещественных корня. Если рассмотреть условие  (
( ),то равенство (5.34) при
),то равенство (5.34) при  не выполняется ни при каких значениях параметров. При любом
не выполняется ни при каких значениях параметров. При любом  условие (5.34) может быть выполнено. Например, при
условие (5.34) может быть выполнено. Например, при  условие (5.34) выполняется для
условие (5.34) выполняется для . (5.35)
. (5.35)
 ,
,  изменяется относительное расположение изоклин, в том числе и положение точки их пересечения, соответствующей стационарному состоянию системы. Три характерных расположения изоклины
изменяется относительное расположение изоклин, в том числе и положение точки их пересечения, соответствующей стационарному состоянию системы. Три характерных расположения изоклины  соответствуют: 1 – устойчивой особой точке; 2– предельному циклу малой амплитуды (квазигармонические колебания); 3 –предельному циклу большой амплитуды (релаксационные колебания). Штриховой линией показаны предельные циклы.
соответствуют: 1 – устойчивой особой точке; 2– предельному циклу малой амплитуды (квазигармонические колебания); 3 –предельному циклу большой амплитуды (релаксационные колебания). Штриховой линией показаны предельные циклы. ,
,  или
или  .
. и
и  , получаем уравнения движения вблизи стационарной точки:
, получаем уравнения движения вблизи стационарной точки: (5.36)
(5.36) ,
,  .
. экспоненциальной во времени эволюции
экспоненциальной во времени эволюции  , (5.37)
, (5.37)


