
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Глава 2. Моделирование физических процессовСодержание книги Поиск на нашем сайте
2.1. Свободное падение тела с учетом сопротивления среды. При реальном движении тела в газовой или жидкостной среде трение накладывает значимый отпечаток на характер движения. Известно, что сила сопротивления среды растет с ростом скорости. В общем случае сила сопротивления определяется суммой линейной и квадратичной составляющих в виде равенства
где Значение коэффициента лобового сопротивления для некоторых тел, поперечное сечение которых имеет указанную на рисунке 2.1 форму приводится ниже.
Рис. 2.1. Значения коэффициента лобового сопротивления При моделировании движения тела с учетом силы сопротивления часто пренебрегают одной из составляющих последней на основании следующих преобразований. Находят значение скорости тела, при которой равны линейная и квадратичная составляющие силы сопротивления:
Если эта скорость существенно (на несколько порядков) меньше чем в исследуемом процессе, то линейной составляющей можно пренебречь. В случае если эта скорость сопоставима со скоростью в исследуемом процессе, то необходимо учитывать и линейную и квадратичную составляющие. Рассмотрим свободное падение с учетом сопротивления среды. Математической моделью движения является уравнение второго закона Ньютона с учетом двух сил, действующих на тело: силы тяжести и силы сопротивления среды:
Проецируя векторное уравнение на ось, направленную вертикально вниз, получим
Учитывая, что скорость есть первая производная от перемещения, окончательно получим следующую систему дифференциальных уравнений, моделирующую свободное падение тела с учетом сопротивления среды:
Определим, как меняется скорость со временем, если все параметры, входящие в систему (2.1) заданы. При наличии сопротивления, растущего со скоростью, в определенный момент времени сила сопротивления сравняется с силой тяжести, после чего скорость больше возрастать не будет. Начиная с этого момента,
Таким образом, при падении скорость тела возрастает от Для решения системы (2.1) используют один из методов численного интегрирования – например метод Эйлера или метод Рунге – Кутта четвертого порядка и на его основе получают приближенные значения величины скорости и высоты тела относительно поверхности Земли, через заданный интервал времени. Приближённое решение системы
на основе метода Эйлера имеет вид:
Метод Рунге – Кутта приближенного решения (2.2) соответственно имеет вид
Ниже приводится код программной модели, которая иллюстрирует движение парашютиста. Программа дает возможность определять координаты парашютиста и его скорость в произвольный момент времени. Кроме того, с ее помощью можно ответить на вопрос на какой высоте лучше всего открывать парашют, чтобы благополучно приземлиться. program desantnik; uses crt,graph; const mu=0.0182; ro=1.29; g=9.8; c=1.33; dt=0.001; m=100; h0=150; hn=522; r=2; str_vv='v='; str_hh='h='; str_tt='t='; str_vmax='vmax='; str_tmax='tmax='; u1=440; u2=640; v1=20; v2=220; u11=440; u22=640; v11=260; v22=460; var h,v0,t,k1,k2,k,kt,kv,kh:extended; k0,u,v,d,adapter,regim:integer; str_v,str_h,str_t,str_1:string; x,y,x_1,x_2,y_1,y_2,i:integer; u1_t,u2_t,v1_v,v2_v,u11_t,u22_t,v1_h,v2_h:integer; tmax,vmax,hmax:integer; t_max,v_max,h_max:extended; function fv(v0,k1,k2:extended):extended; begin fv:=(m*g-k1*v0-k2*sqr(v0))/m; end; function fh(v0:extended):extended; begin fh:=v0; end; procedure desant(u,v:integer; cvet:word); const l1=3; l2=12; l3=6; l4=20; r=2; rp=30; begin setcolor(cvet); circle(u,v,r); rectangle(u-l1,v+r,u+l1,v+r+l2); setfillstyle(solidfill,cvet); floodfill(u,v,cvet); floodfill(u,v+2*r,cvet); line(u-l1,v+r+l2,u-l1,v+r+l2+l3); line(u+l1,v+r+l2,u+l1,v+r+l2+l3); line(u-l1,v+r+l2+l3,round(u-l1-(l3/3)),v+r+l2+l3); line(u+l1,v+r+l2+l3,round(u+l1+(l3/3)),v+r+l2+l3); line(u-l1,v+r,round(u-l1-(l2*sin(pi/6)/(2*cos(pi/6)))), round(v+r+(l2/2))); line(u+l1,v+r,round(u+l1+(l2*sin(pi/6)/(2*cos(pi/6)))), round(v+r+(l2/2))); end; procedure paraschut(u,v:integer; cvet1,cvet2:word); const l1=3; l2=12; l3=6; l4=20; r=2; rp=30; begin desant(u,v,cvet2); setcolor(cvet1); line(u-rp,v-l4,u+rp,v-l4); line(u-rp,v-l4,round(u-l1-(l2*sin(pi/6)/(2*cos(pi/6)))), round(v+r+(l2/2))); line(u+rp,v-l4,round(u+l1+(l2*sin(pi/6)/(2*cos(pi/6)))), round(v+r+(l2/2))); line(round(u-(rp/2)),v-l4,u,round(v+r+l2/2)); line(round(u+(rp/2)),v-l4,u,round(v+r+l2/2)); ellipse(u,v-l4,0,180,rp,round(2*rp/3)); setfillstyle(solidfill,cvet1); floodfill(u,v-l4-2,cvet1); end; procedure zemlya(u,v:integer; cvet1,cvet2:word); const rp=30; begin setcolor(cvet1); ellipse(u-40,v+20,0,180,rp,round(2*rp/3)); line(u-40-rp,v+20,u-40+rp,v+20); setfillstyle(solidfill,cvet1); floodfill(u-40,v+20-round(2*rp/5),cvet1); desant(u,v,cvet2); end; begin clrscr; adapter:=detect; initgraph(adapter,regim,'d:\lang\bp\bgi'); h:=hn; v0:=0; t:=0; k0:=0; k1:=6*pi*mu*r; k2:=c*pi*sqr(r)*ro/2; v_max:=0; repeat t:=t+dt; if h>h0 then begin v0:=v0+fv(v0,0,0)*dt; h:=h-fh(v0)*dt; if v0>v_max then v_max:=v0; end; if h<=h0 then begin v0:=v0+fv(v0,k1,k2)*dt; h:=h-fh(v0)*dt; if v0>v_max then v_max:=v0; end; until h<=0; t_max:=t; h_max:=hn; tmax:=round(t_max); vmax:=round(v_max); hmax:=round(h_max); if tmax mod 10<>0 then tmax:=round(t_max)+(10-(round(t_max) mod 10)); if vmax mod 10<>0 then vmax:=round(v_max)+(10-(round(v_max) mod 10)); if hmax mod 10<>0 then hmax:=round(h_max)+(10-(round(h_max) mod 10)); kt:=10*(u2-u1)/(11*tmax); kv:=10*(v2-v1)/(11*vmax); kh:=10*(v22-v11)/(11*hmax); line(u1,v2,u2,v2); line(u1,v1,u1,v2); line(u2,v2,u2-10,v2-5); line(u2,v2,u2-10,v2+5); line(u1,v1,u1-5,v1+10); line(u1,v1,u1+5,v1+10); outtextxy(u1-5,v2+5,'O'); outtextxy(u1+10,v1,'V'); outtextxy(u2-10,v2-15,'t'); line(u11,v22,u22,v22); line(u11,v11,u11,v22); line(u22,v22,u22-10,v22-5); line(u22,v22,u22-10,v22+5); line(u11,v11,u11-5,v11+10); line(u11,v11,u11+5,v11+10); outtextxy(u11-5,v22+5,'O'); outtextxy(u11+10,v11,'H'); outtextxy(u22-10,v22-15,'t'); for i:=1 to 10 do begin y:=round(v2-(i*(v2-v1)/11)); x_1:=u1-5; x_2:=u1+5; line(x_1,y,x_2,y); str(i*vmax/10:3:0,str_1); outtextxy(u1-40,y,str_1); end; for i:=1 to 10 do begin x:=round(u1+(i*(u2-u1)/11)); y_1:=v2-5; y_2:=v2+5; line(x,y_1,x,y_2); str(i*tmax/10:2:0,str_1); outtextxy(x-10,v2+10,str_1); end; for i:=1 to 10 do begin y:=round(v22-(i*(v22-v11)/11)); x_1:=u11-5; x_2:=u11+5; line(x_1,y,x_2,y); str(i*hmax/10:3:0,str_1); outtextxy(u11-40,y,str_1); end; for i:=1 to 10 do begin x:=round(u11+(i*(u22-u11)/11)); y_1:=v22-5; y_2:=v22+5; line(x,y_1,x,y_2); str(i*tmax/10:2:0,str_1); outtextxy(x-10,v22+10,str_1); end; u:=100; d:=0; k:=460/hn; v:=round(470-k*h); desant(u,v,1); delay(40000); desant(u,v,0); h:=hn; v0:=0; t:=0; u1_t:=round(u1+kt*t); u11_t:=round(u11+kt*t); v1_v:=round(v2-kv*v0); v1_h:=round(v22-kh*hn); repeat t:=t+dt; if h>h0 then begin v0:=v0+fv(v0,0,0)*dt; h:=h-fh(v0)*dt; k0:=k0+1; if k0=round(t_max/(40*dt)) then begin v:=round(460-k*h); desant(u,v,1); delay(40000); desant(u,v,0); setcolor(white); str(v0:6:2,str_v); str(h:6:2,str_h); str(t:6:2,str_t); outtextxy(150,10+d,str_vv+str_v); outtextxy(240,10+d,str_hh+str_h); outtextxy(330,10+d,str_tt+str_t); d:=d+10; k0:=0; u2_t:=round(u1+kt*t); u22_t:=round(u11+kt*t); v2_v:=round(v2-kv*v0); v2_h:=round(v22-kh*h); setcolor(2); line(u1_t,v1_v,u2_t,v2_v); setcolor(3); line(u11_t,v1_h,u22_t,v2_h); u1_t:=u2_t; v1_v:=v2_v; u11_t:=u22_t; v1_h:=v2_h; end; end; if h<=h0 then begin v0:=v0+fv(v0,k1,k2)*dt; h:=h-fh(v0)*dt; k0:=k0+1; if k0=round(t_max/(40*dt)) then begin v:=round(460-k*h); paraschut(u,v,15,1); delay(40000); paraschut(u,v,0,0); setcolor(white); str(v0:6:2,str_v); str(h:6:2,str_h); str(t:6:2,str_t); outtextxy(150,10+d,str_vv+str_v); outtextxy(240,10+d,str_hh+str_h); outtextxy(330,10+d,str_tt+str_t); d:=d+10; k0:=0; u2_t:=round(u1+kt*t); u22_t:=round(u11+kt*t); v2_v:=round(v2-kv*v0); v2_h:=round(v22-kh*h); setcolor(2); line(u1_t,v1_v,u2_t,v2_v); setcolor(3); line(u11_t,v1_h,u22_t,v2_h); u1_t:=u2_t; v1_v:=v2_v; u11_t:=u22_t; v1_h:=v2_h; end; end; until (h<=0) or keypressed; str(v_max:6:2,str_v); outtextxy(10,100,str_vmax+str_v); str(t_max:6:2,str_t); outtextxy(10,200,str_tmax+str_t); delay(40000); zemlya(u,v,15,1); readln; closegraph; end. 2.2. Движение тела с переменной массой: взлет ракеты. Данная задача рассматривается в максимально упрощенной постановке. Основные цели моделирования следующие: 1) Понять, как меняется скорость ракеты во время взлета, как влияют на полет разные факторы. 2) Оценить оптимальное соотношение параметров, при котором ракета достигнет первой космической скорости и сможет вывести на орбиту полезный груз. При моделировании предполагается, что величина силы тяги постоянна на всем этапе разгона. Поскольку ракета очень быстро набирает высокую скорость, то можно пренебречь линейной составляющей силы сопротивления:
где Уравнение второго закона Ньютона с учетом всех сил действующих на ракету имеет вид:
Проецируя данное равенство на вертикальную ось, получим
Поскольку ракета взлетает на высоту в сотни километров, то сила сопротивления в менее плотных слоях атмосферы не может быть такой же, как вблизи поверхности Земли (при равных скоростях). Математически зависимость плотности атмосферы от высоты задается формулой – В итоге система дифференциальных уравнений, описывающая взлет ракеты имеет вид
Данную модель можно усовершенствовать – учесть наличие у ракеты нескольких ступеней, каждая из которых имеет свой запас топлива, и тягу двигателя – считая, что после уменьшения массы до некоторого значения сила тяги изменяется скачком. Полный код программы, моделирующей взлет ракеты, имеет вид: program kosmos; uses crt,graph; const m0=20000000; mk=200000; alfa=200000; beta=0.000129; ft=400000000; g=9.8; ro=1.29; r=2; c=0.4; dt=0.001; str_hh='h='; str_vv='v='; str_tt='t='; u1=400; u2=630; v1=10; v2=220; u11=400; u22=630; v11=240; v22=450; tmax=100; vmax=9000; hmax=150000; var t,v,h,m,s,kt,kv,kh,vvv:extended; rx,ry,yh,yv,yt:longint; adapter,regim,k0,i:integer; x,y,x_1,x_2,y_1,y_2:integer; str_h,str_v,str_t,str_1:string; v_1,t1,v_2,t2,h1,tt1,h2,tt2:longint; function f1(v,m,h:extended):extended; begin f1:=(ft-m*g-(c*ro*exp(-beta*h)*s*v*v/2))/m; end; function f2(v:extended):extended; begin f2:=v; end; procedure raketa(ry,rx:longint; cvet1,cvet2:word); const dh=32; dl=16; dl1=8; dh1=12; rh=2; dog=8; begin setcolor(cvet1); line(rx-dl1,ry,rx,ry-dh1); line(rx,ry-dh1,rx,ry-dh); line(rx+dl,ry-dh,rx+dl,ry-dh1); line(rx+dl,ry-dh1,rx+dl+dl1,ry); line(rx-dl1,ry,rx+dl+dl1,ry); ellipse(rx+round(dl/2),ry-dh,0,180,round(dl/2), round(dl/3)); setfillstyle(solidfill,cvet1); floodfill(round(rx+dl/2),round(ry-dh/2),cvet1); setcolor(cvet2); line(rx-dl1,ry+rh,rx+dl+dl1,ry+rh); line(rx-dl1,ry+rh,trunc(rx+dl/2),ry+rh+dog); line(rx+dl+dl1,ry+rh,trunc(rx+dl/2),ry+rh+dog); setfillstyle(solidfill,cvet2); floodfill(trunc(rx+dl/2),trunc(ry+rh+dog/2),cvet2); end; procedure polet; begin ry:=round(470-(h/320)); raketa(ry,rx,yellow,red); delay(30000); raketa(ry,rx,black,black); end; begin clrscr; adapter:=detect; initgraph(adapter,regim, 'd:\lang\bp\bgi'); rx:=30; ry:=470; t:=0; v:=0; h:=0; k0:=0; s:=pi*r*r; setbkcolor(cyan); raketa(ry,rx,yellow,red); raketa(ry,rx,black,black); setcolor(white); line(u1,v1,u1,v2); line(u1,v2,u2,v2); line(u1,v1,u1-3,v1+5); line(u1,v1,u1+3,v1+5); line(u2,v2,u2-5,v2-3); line(u2,v2,u2-5,v2+3); outtextxy(u1-5,v2+5,'O'); outtextxy(u1+7,v1,'V'); outtextxy(u2,v2+5,'t'); line(u11,v11,u11,v22); line(u11,v22,u22,v22); line(u11,v11,u11-3,v11+5); line(u11,v11,u11+3,v11+5); line(u22,v22,u22-5,v22-3); line(u22,v22,u22-5,v22+3); outtextxy(u11-5,v22+5,'O'); outtextxy(u11+7,v11,'H'); outtextxy(u22,v22+5,'t'); kt:=10*(u2-u1)/(11*tmax); kv:=10*(v2-v1)/(11*vmax); kh:=10*(v22-v11)/(11*hmax); for i:=1 to 10 do begin y:=round(v2-(i*(v2-v1)/11)); x_1:=u1-5; x_2:=u1+5; line(x_1,y,x_2,y); str((vmax/10)*i:4:0,str_1); outtextxy(u1-40,y,str_1); end; for i:=1 to 10 do begin x:=round(u1+(i*(u2-u1)/11)); y_1:=v2-5; y_2:=v2+5; line(x,y_1,x,y_2); str(i*tmax/10:2:0,str_1); outtextxy(x-10,v2+10,str_1); end; for i:=1 to 10 do begin y:=round(v22-(i*(v22-v11)/11)); x_1:=u11-5; x_2:=u11+5; line(x_1,y,x_2,y); str(i*hmax/10:6:0,str_1); outtextxy(u11-60,y,str_1); end; for i:=1 to 10 do begin x:=round(u11+(i*(u22-u11)/11)); y_1:=v22-5; y_2:=v22+5; line(x,y_1,x,y_2); str(i*tmax/10:2:0,str_1); outtextxy(x-10,v22+10,str_1); end; v_1:=v2; t1:=u1; h1:=v22; tt1:=u11; repeat m:=m0-alfa*t; v:=v+f1(v,m,h)*dt; h:=h+f2(v)*dt; setcolor(red); v_2:=round(v2-kv*v); t2:=round(u1+kt*t); line(t1,v_1,t2,v_2); v_1:=v_2; t1:=t2; setcolor(blue); h2:=round(v22-kh*h); tt2:=round(u11+kt*t); line(tt1,h1,tt2,h2); h1:=h2; tt1:=tt2; k0:=k0+1; if k0=3000 then begin polet; setcolor(white); str(h:9:2,str_h); yh:=yh+13; outtextxy(80,yh,str_hh+str_h); str(v:7:2,str_v); yv:=yv+13; outtextxy(190,yv,str_vv+str_v); str(t:3:0,str_t); yt:=yt+13; outtextxy(280,yt,str_tt+str_t); k0:=0; end; t:=t+dt; until (m<=mk) or keypressed; setcolor(white); str(h:9:2,str_h); outtextxy(80,450,str_hh+str_h); str(v:7:2,str_v); outtextxy(190,450,str_vv+str_v); str(t:6:3,str_t); outtextxy(280,450,str_tt+str_t); readln; closegraph; end. 2.3. Движение тела, брошенного под углом к горизонту. Тело, брошенное под углом
Так как движение тела по вертикали происходит под действием постоянной силы тяжести, то оно является равнозамедленным до достижения верхней точки траектории полета и равноускоренным – после нее; движение же по горизонтали является равномерным. Учитывая, что
Общее время движения, без учета сопротивления воздуха, Для нахождения траектории достаточно из текущих значений
следовательно, Полученные формулы могут, в частности, послужить для тестирования будущей компьютерной модели. При достаточно большой начальной скорости сопротивление воздуха может значительно изменить характер движения. Прежде чем выписывать уравнения оценим какая из составляющих силы сопротивления – линейная или квадратичная по скорости – дает больший вклад в эту силу, и нельзя ли одной из этих составляющих пренебречь. Оценку проведем для шарика радиусом Линейная составляющая силы сопротивления равна:
а квадратичная составляющая силы сопротивления
Величины Проецируя уравнение
Поскольку в каждой точке траектории сила сопротивления направлена по касательной к траектории в сторону, противоположную движению, то
где
Далее рассмотрим прием, достаточно популярный в физическом моделировании, называемый обезразмериванием [3]. При решении конкретных задач пользуются определенной системой единиц (СИ), в которой далеко не все числовые значения лежат в удобном диапазоне. Кроме того, абсолютные значения величин не всегда дают достаточно информации для качественного понимания. Идея обезразмеривания заключается в переходе от абсолютных значений расстояний, скоростей, времен и т.д. к относительным, причем отношения строятся к величинам, типичным для данной ситуации. В рассматриваемой задаче при отсутствии сопротивления воздуха имеем значения
– безразмерные расстояния по осям и время, – то при отсутствии сопротивления воздуха переменные Перейдем последовательно от системы (2.3) к системе с безразмерными переменными. Для первого уравнения системы (2.3) имеем:
На основании последнего равенства первое уравнение системы (2.3) преобразуется к виду
Преобразование (2.4) влечет
где Для второго уравнения системы (2.3) имеет место следующий аналог равенства (2.4)
преобразование которого дает второе уравнение в безразмерных переменных:
Для получения третьего уравнения системы имеем
Заменяя в третьем уравнение (2.3)
Для четвертого уравнения справедливо
В результате получена следующая система дифференциальных уравнений
Начальные значения для безразмерных переменных имеют следующих вид:
Важнейшая роль обезразмеривания – установление законов подобия. У изучаемого движения есть множество вариантов, определяемых наборами значений параметров, входящих в систему (2.3) или являющихся для них начальными условиями: Прежде чем начинать численное моделирование, заметим, что при учете лишь линейной составляющей силы сопротивления модель допускает аналитическое решение. Система (2.5) при Разделяя переменные в первом уравнении (2.5) получим
Аналогично решается второе уравнение, а именно,
Заменяя в третьем уравнении (2.5) При решении четвертого уравнения системы (2.5) получаем Таким образом, решение системы (2.5) при
Находя из третьего уравнения системы время
Формула (2.8) не из тех, которые привычно визуализируются, например, по сравнению с совершенно отчетливой формулой Далее приводится код программы, моделирующей движение снаряда, выпущенного из пушки под углом к горизонту из диапазона от нуля до девяноста градусов. program artileriya; uses crt,graph; const g=9.8; ro=1.29; r=0.05; c=0.4; dt=0.01; v_n=100; m=4; mu=0.0182; l_stvola1=50; u0=50; v0=430; umin=u0; umax=300; vmin=220; vmax=v0; u1alfa=150; u2alfa=370; v1l=10; v2l=170; u0alfa=u1alfa; v0l=v2l; str_ll='l='; str_aa='alfa='; str_lmax='lmax='; var adapter,regim,i, x_l1,x_l2,y_l,x_a,y_a1,y_a2:integer; t,vx,vy,vxx,alfa,l,l0,h,s,k1,k2:extended; lmax,hmax,alfalmax,alfahmax,ku,kv,kl,kalfa:extended; k0,u,v,u1_alfa,u2_alfa,v1_l,v2_l, u00,v00,aa,ll,ud:integer; str_l,str_alfa,str_1:string; function fvx(vx,vy:extended):extended; begin fvx:=-(k2*sqrt(sqr(vx)+sqr(vy))+k1)*vx/m; end; function fvy(vx,vy:extended):extended; begin fvy:=(-(k2*sqrt(sqr(vx)+sqr(vy))+k1)*vy/m)-g; end; function fx(vx:extended):extended; begin fx:=vx; end; function fy(vy:extended):extended; begin fy:=vy; end; procedure puschka(cvet:word); const r_stvola=8; r_colesa=20; l_stvola2=40; u1=u0-l_stvola2; u2=u0+l_stvola1; v1=v0-r_stvola; v2=v0+r_stvola; r1=abs(u0-u1); r2=abs(u0-u2); l1=abs(v0-v1); l2=abs(v0-v2); var u_1,v_1,u11,v11,u22,v22,u_2,v_2,u33,v33,u44,v44:integer; begin setcolor(cvet); circle(round(u0+r_colesa*sin(alfa)), round(v0+r_colesa*cos(alfa)),r_colesa); arc(u00,v00,round(90+((alfa*180)/pi)), round(270+((alfa*180)/pi)),r_stvola); u_1:=round(u0-l1*sin(alfa)); v_1:=round(v0-l1*cos(alfa)); u11:=round(u_1-r1*cos(alfa)); v11:=round(v_1+r1*sin(alfa)); u22:=round(u_1+r2*cos(alfa)); v22:=round(v_1-r2*sin(alfa)); u_2:=round(u0+l2*sin(alfa)); v_2:=round(v0+l2*cos(alfa)); u33:=round(u_2+r2*cos(alfa)); v33:=round(v_2-r2*sin(alfa)); u44:=round(u_2-r1*cos(alfa)); v44:=round(v_2+r1*sin(alfa)); line(u11,v11,u22,v22); line(u33,v33,u44,v44); line(u44,v44,u11,v11); setfillstyle(solidfill,cvet); floodfill(round(u0+r_colesa*sin(alfa)), round(v0+r_colesa*cos(alfa)),cvet); floodfill(round(u0-(l_stvola2-2)*cos(alfa)), round(v0+(l_stvola2-2)*sin(alfa)),cvet); floodfill(round(u0+(r_stvola-2)*sin(alfa)), round(v0+(r_stvola-2)*cos(alfa)),cvet); end; procedure polet; const rr=5; begin u:=round(u00+ku*l); v:=round(v00-kv*h); setcolor(red); circle(u,v,rr); setfillstyle(solidfill,red); floodfill(u,v,red); delay(round(100000/(m*v_n))); setcolor(black); circle(u,v,rr); setfillstyle(solidfill,black); floodfill(u,v,black); end; begin clrscr; adapter:=detect; initgraph(adapter,regim,'d:\lang\bp\bgi'); setcolor(white); s:=pi*r*r; k1:=6*pi*mu*r; k2:=c*s*ro/2; lmax:=0; hmax:=0; alfa:=0; alfalmax:=0; alfahmax:=0; repeat t:=0; h:=0; l:=0; vx:=v_n*cos(alfa); vy:=v_n*sin(alfa); repeat vxx:=vx; vx:=vx+dt*fvx(vx,vy); vy:=vy+dt*fvy(vxx,vy); l:=l+dt*fx(vx); h:=h+dt*fy(vy); t:=t+dt; if alfa=0 then l0:=l; if h>=hmax then begin hmax:=h; alfahmax:=alfa; end; until (h<=0) and (t>0); if l>=lmax then begin lmax:=l; alfalmax:=alfa; end; alfa:=alfa+(pi/180); until alfa>=pi/2; ku:=(umax-umin)/lmax; kv:=(vmax-vmin)/hmax; kalfa:=9*(u2alfa-u1alfa)/(5*pi); kl:=(v2l-v1l)/(10*lmax/9); line(u1alfa,v1l,u1alfa,v2l); line(u1alfa,v2l,u2alfa,v2l); line(u2alfa,v2l,u2alfa-10,v2l+5); line(u2alfa,v2l,u2alfa-10,v2l-5); line(u1alfa,v1l,u1alfa-5,v1l+10); line(u1alfa,v1l,u1alfa+5,v1l+10); outtextxy(u2alfa-25,v2l-17,'ALFA'); outtextxy(u1alfa-15,v1l,'L'); outtextxy(u1alfa-5,v2l+5,'O'); for i:=1 to 9 do begin y_l:=round(v2l-(i*(v2l-v1l)/10)); x_l1:=u1alfa-5; x_l2:=u1alfa+5; line(x_l1,y_l,x_l2,y_l); str(i*round(lmax/9):4,str_1); outtextxy(u1alfa-40,y_l,str_1); end; for i:=1 to 9 do begin x_a:=round(u1alfa+(i*(u2alfa-u1alfa)/10)); y_a1:=v2l-5; y_a2:=v2l+5; line(x_a,y_a1,x_a,y_a2); str((10*i):2,str_1); outtextxy(x_a-5,v2l+10,str_1); end; alfa:=0; u1_alfa:=round(u0alfa+kalfa*alfa); v1_l:=round(v0l-kl*l0); aa:=0; ll:=0; ud:=0; repeat t:=0; h:=0; l:=0; k0:=0; vx:=v_n*cos(alfa); vy:=v_n*sin(alfa); u00:=round(u0+l_stvola1*cos(alfa)); v00:=round(v0-l_stvola1*sin(alfa)); puschka(6); polet; repeat vxx:=vx; vx:=vx+dt*fvx(vx,vy); vy:=vy+dt*fvy(vxx,vy); l:=l+dt*fx(vx); h:=h+dt*fy(vy); t:=t+dt; k0:=k0+1; if k0=3 then begin polet; k0:=0; end; until (h<=0) and (t>0); puschka(0); setcolor(red); str((180*alfa/pi):2:0,str_alfa); outtextxy(380+ud,aa,str_aa+str_alfa); aa:=aa+10; str(l:4:0,str_l); outtextxy(450+ud,ll,str_ll+str_l); ll:=ll+10; if round(180*alfa/pi)=45 then begin ud:=140; aa:=0; ll:=0; end; u2_alfa:=round(u0alfa+kalfa*alfa); v2_l:=round(v0l-kl*l); line(u1_alfa,v1_l,u2_alfa,v2_l); u1_alfa:=u2_alfa; v1_l:=v2_l; alfa:=alfa+(pi/180); until (round(180*alfa/pi)>90) or keypressed; str(lmax:8:3,str_l); outtextxy(60,300,str_lmax+str_l); str(round(180*alfalmax/pi):2,str_alfa); outtextxy(60,350,str_aa+str_alfa); readln; closegraph; end. 2.4. Движение небесных тел. Законы Кеплера. Движение заряженных частиц. По закону всемирного тяготения сила притяжения, действующая между двумя телами, пропорциональна их массам и обратно пропорциональна квадрату расстояния между ними. Если поместить начало системы координат на одном из тел (размерами тел по сравнению с расстоянием между ними будем пренебрегать), математическая запись силы, действующей на второе тело, имеет вид
где
Рис. 2.2. Выбор системы координат при решении задачи двух тел Знак «минус» в формуле (2.9) связан с тем, что гравитационная сила является силой притяжения, т.е. стремится уменьшить расстояние Далее ограничимся изучением взаимного движения двух тел. Рассмотрим движение одного из тел с точки зрения наблюдателя, находящегося на втором, т.е., например, движения планеты или кометы относительно Солнца, Луны относительно Земли, пренебрегая при этом относительно небольшими силами притяжения от всех прочих небесных тел. Уравнение, описывающее движение тела массой
или в проекциях на оси
Очень часто космические тела движутся практически с постоянной скоростью по орбитам, близким к круговым. Для таких орбит легко найти элементарное соотношение между скоростью и радиусом. В этом случае сила тяготения выступает в роли центростремительной, а центростремительная сила при постоянной скорости выражается известной из курса физики формулой
Период движения по такой орбите определяется равенством Отсюда вытекает один из законов Кеплера: отношение кубов радиусов орбит любых двух планет Солнечной системы равно отношению квадратов периодов их обращения вокруг Солнца, т.е.
Возможными траекториями движения, описываемые системой (2.12), являются эллипс, парабола и гипербола. Законы Кеплера 1) Всякая планета движется по эллиптической орбите с общим фокусом, в котором находится Солнце. 2) Каждая планета движется так, что ее радиус-вектор за одинаковые промежутки времени описывает равные площади; на рисунке 2.3 промежутки времени движения от
Рис. 2.3. Иллюстрация второго закона Кеплера 3) Отношение кубов больших полуосей орбит двух любых планет солнечной системы равно отношению квадратов периодов их обращения вокруг Солнца. Система (2.12) описывает движение не только планет, но и любых тел, попадающих в поле тяготения большой массы. Так, в Солнечной системе существует большое количество комет, движущихся по чрезвычайно вытянутым эллиптическим орбитам с периодами от нескольких земных лет до нескольких миллионов земных лет. Траектория небесных тел, не являющихся постоянными членами Солнечной системы, а залетевших в нее издалека, определяется их скоростью – если она достаточно велика, то орбита будет гиперболической, и, облетев Солнце, тело покинет Солнечную систему, если нет – перейдет на эллиптическую орбиту и станет частью системы; пограничная между ними орбита – параболическая. Закон Кулона, описывающий взаимодействие двух точечных зарядов Рассмотрим задачу – движение «малого» заряда некоторого знака в поле, созданным «большим» неподвижным зарядом другого знака [3]. Эта задача после обезразмеривания уравнений в точности такая же, как и описанная выше задача движения «малого» небесного тела. В общем случае данная задача описывается следующей системой дифференциальных уравнений
В электростатике рассматривается широкий круг задач, не имеющих аналога в гравитации. Простейшими из них являются следующие: 1. Движение «малого» заряда в поле «большого» при взаимном отталкивании. 2. Движение заряженного тела в поле, созданном несколькими фиксированными зарядами произвольных знаков (заряды могут лежать как в одной плоскости, так и в разных). 3. Движение заряженного тела между пластинами конденсатора. При решении последней задачи закон Кулона нельзя применить напрямую, потому что заряженная пластина не может рассматриваться как точечных заряд. При моделировании можно воспользоваться следующим приемом: разбить пластину на «элементарные» квадраты, каждому из которых приписать заряд и заменить пластину набором «точечных зарядов», взаимодействующих с пролетающей частицей. 2.5. Колебания математического маятника. Колебательное движение – одно из самых распространенных в природе. Разнообразные маятники в часах и других технических устройствах, колебания мембран и
|
||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 355; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.186.27 (0.01 с.) |

 ,
, определяется свойствами среды и формой тела. Например, для шарика
определяется свойствами среды и формой тела. Например, для шарика  – формула Стокса, где
– формула Стокса, где 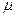 – динамическая вязкость среды,
– динамическая вязкость среды, 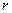 – радиус шарика (для воздуха при t = 20°C и давлении 1 атм
– радиус шарика (для воздуха при t = 20°C и давлении 1 атм  , для воды
, для воды 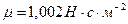 , для глицерина
, для глицерина  ); величина
); величина 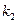 определяется равенством
определяется равенством 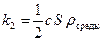 , где
, где  – коэффициент лобового сопротивления (безразмерен),
– коэффициент лобового сопротивления (безразмерен),  – площадь поперечного сечения тела,
– площадь поперечного сечения тела,  – плотность среды.
– плотность среды.
 ,
, 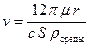 .
. или
или 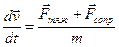 .
. .
. (2.1)
(2.1) , и установившаяся скорость
, и установившаяся скорость  определяется из условия
определяется из условия 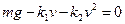 . Решая квадратное уравнение, получим
. Решая квадратное уравнение, получим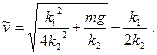
 до
до  (2.2)
(2.2)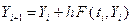 ,
, 
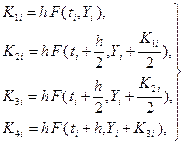
 ,
,  . Кроме того, необходимо учесть убывание массы ракеты в процессе взлета. Будем считать, что топливо расходуется равномерно вплоть до его полного выгорания:
. Кроме того, необходимо учесть убывание массы ракеты в процессе взлета. Будем считать, что топливо расходуется равномерно вплоть до его полного выгорания:
 – начальная масса ракеты,
– начальная масса ракеты,  – масса полезного груза, выводимо на орбиту,
– масса полезного груза, выводимо на орбиту,  – расход топлива.
– расход топлива.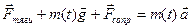 .
. .
. , где
, где  .
.
 ,
,  .
.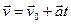 , проекция вектора скорости на вертикальную ось имеет вид
, проекция вектора скорости на вертикальную ось имеет вид  . Так как в верхней точке траектории
. Так как в верхней точке траектории  , то время подъема определяется равенством
, то время подъема определяется равенством  . Зная время подъема можно найти на какую максимальную высоту поднимется тело:
. Зная время подъема можно найти на какую максимальную высоту поднимется тело:  . Проецируя уравнение на вертикальную ось, получим:
. Проецируя уравнение на вертикальную ось, получим: . Отсюда следует, что
. Отсюда следует, что  .
.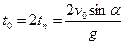 . За это время, двигаясь равномерно вдоль оси
. За это время, двигаясь равномерно вдоль оси 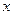 со скоростью
со скоростью  , тело пройдет путь
, тело пройдет путь  или
или  .
. исключить
исключить  :
: ,
,  ;
; . На основании последнего равенства в частности делается вывод о том, что траекторией движения тела брошенного под углом к горизонту является парабола.
. На основании последнего равенства в частности делается вывод о том, что траекторией движения тела брошенного под углом к горизонту является парабола. , движущегося со скоростью 1 м/с. По порядку величины оценка не зависит от формы тела.
, движущегося со скоростью 1 м/с. По порядку величины оценка не зависит от формы тела. ,
, .
. и
и 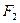 сопоставимые (так как они различаются менее чем в 5 раз). При увеличении размера тела
сопоставимые (так как они различаются менее чем в 5 раз). При увеличении размера тела  ,
,  ), при увеличении скорости
), при увеличении скорости 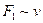 ,
,  ). Таким образом, если мы моделируем движение брошенного мяча или камня, то необходимо в уравнениях учитывать обе составляющие силы сопротивления, но если моделировать полет снаряда, выпущенного из орудия, где скорость полета почти на всем его протяжении сотни метров в секунду, то линейной составляющей силы сопротивления можно пренебречь.
). Таким образом, если мы моделируем движение брошенного мяча или камня, то необходимо в уравнениях учитывать обе составляющие силы сопротивления, но если моделировать полет снаряда, выпущенного из орудия, где скорость полета почти на всем его протяжении сотни метров в секунду, то линейной составляющей силы сопротивления можно пренебречь. на оси
на оси 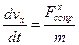 ,
,  .
. ,
, ,
,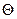 – угол между текущим направлением скорости и осью х. Подставляя это в уравнение и учитывая, что
– угол между текущим направлением скорости и осью х. Подставляя это в уравнение и учитывая, что  , и
, и  ,
,  получаем систему дифференциальных уравнений моделирующую движение тела под углом к горизонту с учетом силы сопротивления:
получаем систему дифференциальных уравнений моделирующую движение тела под углом к горизонту с учетом силы сопротивления: (2.3)
(2.3) ,
,  ,
,  , определенные выше; сопротивление воздуха изменит характер движения, и если ввести в качестве переменных величины
, определенные выше; сопротивление воздуха изменит характер движения, и если ввести в качестве переменных величины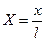 ,
,  ,
, 
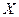 ,
,  будут изменяться в диапазоне от 0 до 1, а в задаче с учетом сопротивления отличия их максимальных значений от единицы ясно характеризуют влияние этого сопротивления. Для скоростей вводятся безразмерные переменные, равные отношению проекции скорости на оси
будут изменяться в диапазоне от 0 до 1, а в задаче с учетом сопротивления отличия их максимальных значений от единицы ясно характеризуют влияние этого сопротивления. Для скоростей вводятся безразмерные переменные, равные отношению проекции скорости на оси 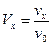 ,
,  .
. .
. . (2.4)
. (2.4) ,
, ,
,  .
. ,
, .
. .
. на
на  , получим
, получим , или
, или  .
.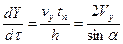 .
. (2.5)
(2.5) ,
,  ,
,  ,
,  .
. ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  физически легче интерпретировать, чем их размерные аналоги, так как они измеряются относительно величин, смысл которых очевиден.
физически легче интерпретировать, чем их размерные аналоги, так как они измеряются относительно величин, смысл которых очевиден. сравнительно элементарно интегрируется.
сравнительно элементарно интегрируется. . Отсюда
. Отсюда  или
или  . Учитывая, что
. Учитывая, что  окончательно получаем, что
окончательно получаем, что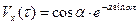 . (2.6)
. (2.6) . Интегрируя последнее равенство, получим
. Интегрируя последнее равенство, получим  . Отсюда следует, что
. Отсюда следует, что  . С учетом начального условия решение второго уравнения (2.5) имеет вид:
. С учетом начального условия решение второго уравнения (2.5) имеет вид: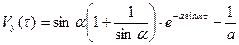 .
. . Решение этого уравнения имеет вид
. Решение этого уравнения имеет вид  . С учетом начального условия получим
. С учетом начального условия получим  .
. . Отсюда следует, что
. Отсюда следует, что  . Окончательно с учетом начального условия, получаем
. Окончательно с учетом начального условия, получаем  .
. (2.7)
(2.7) ) и подставляя его в последнее уравнение системы (2.7) получаем уравнение траектории
) и подставляя его в последнее уравнение системы (2.7) получаем уравнение траектории . (2.8)
. (2.8) , (2.9)
, (2.9)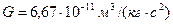 – гравитационная постоянная.
– гравитационная постоянная.
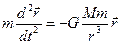
 ,
,  . (2.10)
. (2.10) . Таким образом, имеем
. Таким образом, имеем или
или 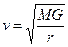 . (2.11)
. (2.11) .
. . Если соотношение (2.11) нарушено, то орбита не будет круговой. Выяснить какой она будет, можно в ходе численного моделирования. Для этого сведем (2.10) к системе из четырех дифференциальных уравнений первого порядка:
. Если соотношение (2.11) нарушено, то орбита не будет круговой. Выяснить какой она будет, можно в ходе численного моделирования. Для этого сведем (2.10) к системе из четырех дифференциальных уравнений первого порядка: (2.12)
(2.12) к
к  , и от
, и от  к
к  считаются одинаковыми, а площади секторов
считаются одинаковыми, а площади секторов  и
и  равны. Это означает, что чем ближе планета к Солнцу, тем у нее больше скорость движения по орбите.
равны. Это означает, что чем ближе планета к Солнцу, тем у нее больше скорость движения по орбите.
 и
и  имеет вид
имеет вид  , где
, где  – электрическая постоянная.
– электрическая постоянная.



