Методология компьютерного моделирования

ВВЕДЕНИЕ

Среда разработки лабораторных виртуальных приборов LabVIEW (Laboratory Virtual Instrument Engineering Workbench) представляет собой среду прикладного графического программирования, используемую в качестве стандартного инструмента для проведения измерений, анализа их данных и последующего управления приборами и исследуемыми объектами. LabVIEW может использоваться на компьютерах с операционными системами Windows, MacOS, Linux, Solaris и HP-UX. Компьютер, оснащенный измерительно-управляющей аппаратной частью и LabVIEW, позволяет полностью автоматизировать процесс физических исследований. Создание любой программы для достижения этих целей (виртуального прибора) в графической среде LabVIEW отличается большой простотой, поскольку исключает множество синтаксических деталей.

Особо следует отметить динамику развития LabVIEW. Первая его версия была создана в 1986 году компанией National Instruments в результате поисков путей сокращения времени программирования измерительных приборов. Версии LabVIEW с второй по седьмую проявлялись в 1990, 1992, 1993, 1996, 2000 и 2003 годах. Каждая последующая существенно расширяла возможности предыдущей версии и прежде всего по обмену данных с измерительными приборами и работе с другими программными продуктами.

Сфера применимости LabVIEW также непрерывно расширяется. В образовании она включает лабораторные практикумы по электротехнике, механике, физике. В фундаментальной науке LabVIEW используют такие передовые центры как CERN (в Европе), Lawrence Livermore, Batelle, Sandia, Oak Ridge (США), в инженерной практике - объекты космические, воздушного, надводного и подводного флота, промышленные предприятия и т.д.

LabVIEW является идеальным программным средством для создания систем измерения, а также систем автоматизации управления на основе технологии виртуальных приборов. LabVIEW-программа в комплексе с такими аппаратными средствами, как встраиваемые в компьютер многоканальные измерительные аналого-цифровые платы, платы захвата и синхронизации видеоизображения для систем машинного зрения, платы управления движением и исполнительные механизмы, а также измерительные приборы, подключаемые к компьютеру через стандартные интерфейсы RS-232, RS-485, USB, GPIB (КОП), PXI, VXI, позволяет разрабатывать системы измерения, контроля, диагностики и управления практически любой сложности.

1 теоретические вопросы

1.1 Структура процесса моделирования

Сложная система рассматривается как целостная совокупность элементов, характеризующаяся наличием большого количества взаимосвязанных и взаимодействующих между собой элементов.

У исследователя существует субъективная возможность разбиения системы на подсистемы, цели функционирования которых подчинены общей цели функционирования всей системы (целенаправленность систем). Целенаправленность интерпретируется, как способность системы осуществлять в условиях неопределенности и воздействия случайных факторов поведение (выбор поведения), преследующее достижение определенной цели.

 

Понятие модели

Модель представляет собой абстрактное описание системы (объекта, процесса, проблемы, понятия) в некоторой форме, отличной от формы их реального существования.

Моделированиепредставляет собой один из основных методов познания, является формой отражения действительности и заключается в выяснении или воспроизведении тех или иных свойств реальных объектов, предметов и явлений с помощью других объектов, процессов, явлений, либо с помощью абстрактного описания в виде изображения, плана, карты, совокупности уравнений, алгоритмов и программ.

В процессе моделирования всегда существует оригинал (объект) и модель, которая воспроизводит (моделирует, описывает, имитирует) некоторые черты объекта.

Моделирование основано на наличии у многообразия естественных и искусственных систем, отличающихся как целевым назначением, так и физическим воплощением, сходства или подобия некоторых свойств: геометрических, структурных, функциональных, поведенческих. Это сходство может быть полным (изоморфизм)и частичным (гомоморфизм).

 

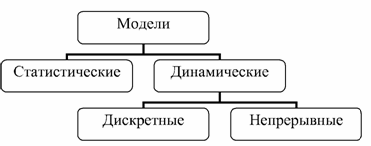
Классификация моделей

Существует большое количество классификаций моделей. Приведем некоторые из них.

С учетом фактора времени:

Статистические модели — модели, описывающие состояние модели в определенный момент времени. В физике примером статистической модели может быть движение молекул, в химии — модели строения атомов, в биологии — модели классификации животных.

Динамические модели — модели, описывающие процессы изменения и развития системы с течением времени. В физике примером динамической модели может быть движение тел, в химии — процессы происхождения химических реакций, в биологии — развитие организмов.

По способу представления:

Материальные — воспроизводят геометрические, физические и др. свойства объектов в материальной форме. Они основаны на чем-то существующем независимо от человеческого сознания. Физические модели: авто- и авиамодели, глобус, здания и т. д.

Аналоговые модели основаны на процессах, аналогичных изучаемым процессам. Например, электрическая цепь как аналогия химических, социальных цепей.

Физической моделью процесса или явления называется его математическая модель, составленная из идеальных физических объектов.

Информационная модель — описание реального объекта, процесса или явления на одном из языков (разговорном или формальном).

Образные информационные модели — это зрительные образы (рисунки, фотографии), зафиксированные на каком-либо носителе информации (бумаге, пленке и прочем). Они широко используются в образовании и науках, где требуется классификация объектов по их внешним признакам.

Знаковые информационные модели строятся с использованием различных языков. Знаковая информация может быть представ- лена в виде текста, формул, таблиц и т. д.

Геометрические модели — модели, представленные в виде объемных конструкций или графических форм.

Словесные модели — модели, выраженные устно или письменно.

Математические модели — модели, записанные с помощью уравнений, математических формул, неравенств, систем и т. п.

Структурные модели — схемы, графики, таблицы и т. п.

Логические модели — модели, в которых принимаются решения на основе анализа различных условий.

Специальные модели — ноты, химические формулы и т. п.

Компьютерные модели — модели, реализованные на компьютере с помощью программного обеспечения.

Формализация — процесс построения информационной модели.

Приведем общую классификацию основных видов моделирования:

· концептуальное моделирование– представление системы с помощью специальных знаков, символов, операций над ними или с помощью естественных или искусственных языков;

· физическое моделирование– моделируемый объект или процесс воспроизводится исходя из соотношения подобия, вытекающего из схожести физических процессов и явлений;

· структурно – функциональное моделирование – моделями являются схемы (графы, блок-схемы), графики, диаграммы, таблицы, рисунки со специальными правилами их объединения и преобразования;

· математическое (логико-математическое) моделирование– построение модели осуществляется средствами математики и логики;

· имитационное (программное) моделирование– в этом случае логико-математическая модель исследуемой системы представляет собой алгоритм функционирования системы, программно-реализуемый на компьютере.

Указанные виды моделирования могут применяться самостоятельно или одновременно, в некоторой комбинации (например, в имитационном моделировании используются практически все перечисленные виды моделирования или отдельные приемы). Так, например, имитационное моделирование включает в себя концептуальное (на ранних этапах формирования имитационной модели) и логико-математическое (включая методы искусственного интеллекта) моделирование для описания отдельных подсистем модели, а также в процедурах обработки и анализа результатов вычислительного эксперимента и принятия решений. Технология проведения и планирования вычислительного эксперимента с соответствующими математическими методами привнесена в имитационное моделирование из физического (экспериментального натурного или лабораторного) моделирования. Наконец, структурно-функциональное моделирование используется как при создании стратифицированного описания многомодельных комплексов, так и для формирования различных диаграммных представлений при создании имитационных моделей.

Понятие компьютерного моделирования трактуется шире традиционного понятия “моделирование на ЭВМ”. Приведем его.

 

Компьютерное моделирование

Методологией исследования СС является системный анализ. Один из важнейших инструментов прикладного системного анализа – компьютерное моделирование.
Имитационное моделирование является наиболее эффективным и универсальным вариантом компьютерного моделирования в области исследования и управления сложными системами.

Компьютерное моделирование– это метод решения задач анализа или синтеза сложной системы на основе использования ее компьютерной модели.

Компьютерное моделирование можно рассматривать как:

· математическое моделирование;

· имитационное моделирование;

· стохастическое моделирование.

Под термином “компьютерная модель” понимают условный образ объекта или некоторой системы объектов (или процессов), описанный с помощью уравнений, неравенств, логических соотношений, взаимосвязанных компьютерных таблиц, графов, диаграмм, графиков, рисунков, анимационных фрагментов, гипертекстов и т.д. и отображающих структуру и взаимосвязи между элементами объекта. Компьютерные модели, описанные с помощью уравнений, неравенств, логических соотношений, взаимосвязанных компьютерных таблиц, графов, диаграмм, графиков, будем называть математическими. Компьютерные модели, описанные с помощью взаимосвязанных компьютерных таблиц, графов, диаграмм, графиков, рисунков, анимационных фрагментов, гипертекстов и т.д. и отображающих структуру и взаимосвязи между элементами объекта, будем называть структурно-функциональными;

Компьютерные модели (отдельную программу, совокупность программ, программный комплекс), позволяющие, с помощью последовательности вычислений и графического отображения результатов ее работы, воспроизводить (имитировать) процессы функционирования объекта (системы объектов) при условии воздействия на объект различных, как правило, случайных факторов, будем называть имитационными.

Суть компьютерного моделирования заключена в получении количественных и качественных результатов на имеющейся модели. Качественные результаты анализа обнаруживают неизвестные ранее свойства сложной системы: ее структуру, динамику развития, устойчивость, целостность и др. Количественные выводы в основном носят характер анализа существующей СС или прогноза будущих значений некоторых переменных. Возможность получения не только качественных, но и количественных результатов составляет существенное отличие имитационного моделирования от структурно-функционального.

 

Разработка нулевого кадра.

На нулевом кадре реализуется запуск ВП с помощью кнопки «Старт». Для этого используем структуру «While loop» (Меню>>Window>>Show Functions Palette>>Structures>>While loop) и помещаем ее внутрь нулевого кадра. С помощью катушки (Connect Wire) соединяем кнопку «старт» с Stop If True.

Рисунок 21. Разработка нулевого кадра.

 

Разработка первого кадра.

Первый кадр отвечает за запуск таймера при включении прибора.

Таймер будет отсчитывать время с нажатием на кнопку «старт» и остановится с нажатием на кнопку «стоп». Для этого в первый кадр добавляем элемент «Tick Count (ms)» (Меню>>Window>>Show Functions Palette>>Time & Dialog>>Tick Count (ms)).

Для передачи данных в «Sequence Structure» с первого кадра на последующие необходимо добавить элемент «Sequence Local». Для это нажимаем на границу «Sequence Structure» правой копкой мыши и в всплывающем окне выбираем «Sequence Local». Затем с помощью катушки (Connect Wire) соединяем «Sequence Local» с таймером.

Рисунок 22. Разработка нулевого кадра.

 

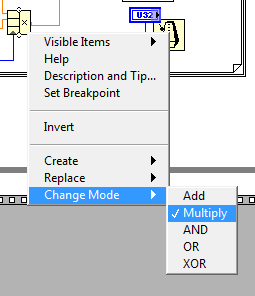
Разработка второго кадра.

Второй кадр основной. Он отвечает за работоспособность всего виртуального прибора.

Добавляем в кадр структуру «While loop» (Меню>>Window>>Show Functions Palette>>Structures>>While loop). С помощью катушки (Connect Wire) соединяем кнопку «стоп» с Stop If True.. Внутрь цикла «While loop» перемещаем регулятор частоты, регулятор амплитуды шума, график. Так же внутрь цикла «While loop» добавляем еще один цикл «For Loop» (Меню>>Window>>Show Functions Palette>>Structures>> For Loop).

В цикл «For Loop» добавляем генератор случайных чисел Меню>>Window>>Show Functions Palette>>Numeric>>Random Number (0-1).

Генератор случайных чисел соеденяем через Miltiplay (Меню>>Numeric>> Miltiplay) с регулятором частоты. Для этого с помощью катушки (Connect Wire) соединяем «регулятор частоты» с границей цикла «For Loop» на ней образуется контакт, далее этот контакт соединяем с контактом Multiplay, второй контакт Multiplay будет подключен к генератору случайных чисел.

Регулятор амплитуды шума так же с помощью катушки соеденяем с границей цикла «For Loop». Далее в цикл «For Loop» добавляем элемент Compound Arifmetic (Меню>>Numeric>> Compound Arifmetic). Нажимаем на появившейся элемент правой кнопкой мыши, в всплывающем окне заходим Change Mode и выбираем Multiplay(Рисунок 23). Таким образом, новый элемент должен содержать три входных сигнала, и один выходной (Multiplay).

Рисунок 23.

В цикл «While loop» добавляем элемент Divide(Меню>>Numeric>> Divide). Рядом добавляем еще один элемент «Pi Multiplied By 2» (Меню>>Numeric>> Additional Numeric Constants>> Pi Multiplied By 2). Соединяем остальное, как показано на рисунке 24.

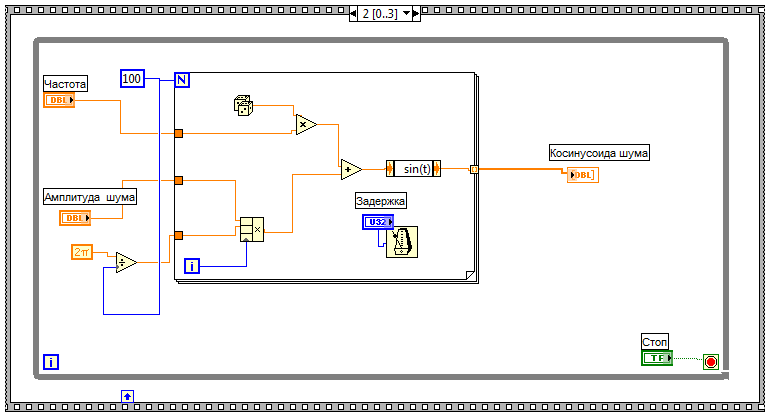
Рисунок 24.

Добавляем элемент «Add»(Меню>>Numeric>>Add), два входных сигнала соединяем с помощью катушки с элементами: «Multiplay» и «Compound Arifmetic». Далее добавляем элемент «Expression Node»(Меню>>Numeric>> Expression Node). С помощью катушки соединяем элемент «Add» с элементом «Expression Node».Узел выражения (Expression Node) используется для вычисления арифметических выражений, или равенств, которые содержат одну единственную переменную. Узел выражения удобен, когда равенство хоть и содержит только одну переменную, но является достаточно сложным.

В элемент «Expression Node» с помощью функции «Edit Text» вписываем выражение: sin(t).

С помощью катушки соединяем «Expression Node» с границей цикла «While loop». Образовавшийся контакт соединяем с графиком.

Для более детальной наглядности зависимости графика установим задержку. Для это добавим новый элемент Меню>>Window>>Show Functions Palette>>Time & Dialog>>Wait Until next ms Multiple.

Рисунок 25. Разработка второго кадра.

Разработка третьего кадра.

Третий кадр отвечает за остановку таймера времени после нажатии кнопки стоп и отображения этого времени на цифровом индикаторе.

Добавляем в кадр «Tick Count (ms)» (Меню>>Window>>Show Functions Palette>>Time & Dialog>>Tick Count (ms)). Для того что бы он функционировал с нулевым кадром соединяем их через элемент «Subtract» (Меню>>Numeric>> Subtract). Так как время у нас будет отображаться в миллисекундах, то нам нужно преобразовать их в секунды. Для этого добавляем элемент «Add», один контакт соединяем с элементом «Subtract», а из второго выводим константу равную 1000. Таким образом, получается, что полученный результат в миллисекундах будет делится на 1000 и тем самым переведется в секунды. Далее добавляем цифровой индикатором и соединяем с элементом «Add».

Рисунок 26. Разработка третьего кадра.

Прибор готов к работе.

 

СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ

1) Васильев В. Г.Моделирование систем автоматического управления в программной среде LabVIEW. – Тверь, 2007. – 25 c.

2) Жуков К. Г. Модельное проектирование встраиваемых систем в LabVIEW. –М.: ДМК Пресс, 2011. – 688 с.

3) http://www.infosgs.narod.ru/34.htm

4) http://ru.wikipedia.org/wiki/LabVIEW

5) http://rose.somee.com/labview/default.aspx

 

ВВЕДЕНИЕ

Среда разработки лабораторных виртуальных приборов LabVIEW (Laboratory Virtual Instrument Engineering Workbench) представляет собой среду прикладного графического программирования, используемую в качестве стандартного инструмента для проведения измерений, анализа их данных и последующего управления приборами и исследуемыми объектами. LabVIEW может использоваться на компьютерах с операционными системами Windows, MacOS, Linux, Solaris и HP-UX. Компьютер, оснащенный измерительно-управляющей аппаратной частью и LabVIEW, позволяет полностью автоматизировать процесс физических исследований. Создание любой программы для достижения этих целей (виртуального прибора) в графической среде LabVIEW отличается большой простотой, поскольку исключает множество синтаксических деталей.

Особо следует отметить динамику развития LabVIEW. Первая его версия была создана в 1986 году компанией National Instruments в результате поисков путей сокращения времени программирования измерительных приборов. Версии LabVIEW с второй по седьмую проявлялись в 1990, 1992, 1993, 1996, 2000 и 2003 годах. Каждая последующая существенно расширяла возможности предыдущей версии и прежде всего по обмену данных с измерительными приборами и работе с другими программными продуктами.

Сфера применимости LabVIEW также непрерывно расширяется. В образовании она включает лабораторные практикумы по электротехнике, механике, физике. В фундаментальной науке LabVIEW используют такие передовые центры как CERN (в Европе), Lawrence Livermore, Batelle, Sandia, Oak Ridge (США), в инженерной практике - объекты космические, воздушного, надводного и подводного флота, промышленные предприятия и т.д.

LabVIEW является идеальным программным средством для создания систем измерения, а также систем автоматизации управления на основе технологии виртуальных приборов. LabVIEW-программа в комплексе с такими аппаратными средствами, как встраиваемые в компьютер многоканальные измерительные аналого-цифровые платы, платы захвата и синхронизации видеоизображения для систем машинного зрения, платы управления движением и исполнительные механизмы, а также измерительные приборы, подключаемые к компьютеру через стандартные интерфейсы RS-232, RS-485, USB, GPIB (КОП), PXI, VXI, позволяет разрабатывать системы измерения, контроля, диагностики и управления практически любой сложности.

1 теоретические вопросы

1.1 Структура процесса моделирования

Сложная система рассматривается как целостная совокупность элементов, характеризующаяся наличием большого количества взаимосвязанных и взаимодействующих между собой элементов.

У исследователя существует субъективная возможность разбиения системы на подсистемы, цели функционирования которых подчинены общей цели функционирования всей системы (целенаправленность систем). Целенаправленность интерпретируется, как способность системы осуществлять в условиях неопределенности и воздействия случайных факторов поведение (выбор поведения), преследующее достижение определенной цели.

 

Понятие модели

Модель представляет собой абстрактное описание системы (объекта, процесса, проблемы, понятия) в некоторой форме, отличной от формы их реального существования.

Моделированиепредставляет собой один из основных методов познания, является формой отражения действительности и заключается в выяснении или воспроизведении тех или иных свойств реальных объектов, предметов и явлений с помощью других объектов, процессов, явлений, либо с помощью абстрактного описания в виде изображения, плана, карты, совокупности уравнений, алгоритмов и программ.

В процессе моделирования всегда существует оригинал (объект) и модель, которая воспроизводит (моделирует, описывает, имитирует) некоторые черты объекта.

Моделирование основано на наличии у многообразия естественных и искусственных систем, отличающихся как целевым назначением, так и физическим воплощением, сходства или подобия некоторых свойств: геометрических, структурных, функциональных, поведенческих. Это сходство может быть полным (изоморфизм)и частичным (гомоморфизм).

 

Классификация моделей

Существует большое количество классификаций моделей. Приведем некоторые из них.

С учетом фактора времени:

Статистические модели — модели, описывающие состояние модели в определенный момент времени. В физике примером статистической модели может быть движение молекул, в химии — модели строения атомов, в биологии — модели классификации животных.

Динамические модели — модели, описывающие процессы изменения и развития системы с течением времени. В физике примером динамической модели может быть движение тел, в химии — процессы происхождения химических реакций, в биологии — развитие организмов.

По способу представления:

Материальные — воспроизводят геометрические, физические и др. свойства объектов в материальной форме. Они основаны на чем-то существующем независимо от человеческого сознания. Физические модели: авто- и авиамодели, глобус, здания и т. д.

Аналоговые модели основаны на процессах, аналогичных изучаемым процессам. Например, электрическая цепь как аналогия химических, социальных цепей.

Физической моделью процесса или явления называется его математическая модель, составленная из идеальных физических объектов.

Информационная модель — описание реального объекта, процесса или явления на одном из языков (разговорном или формальном).

Образные информационные модели — это зрительные образы (рисунки, фотографии), зафиксированные на каком-либо носителе информации (бумаге, пленке и прочем). Они широко используются в образовании и науках, где требуется классификация объектов по их внешним признакам.

Знаковые информационные модели строятся с использованием различных языков. Знаковая информация может быть представ- лена в виде текста, формул, таблиц и т. д.

Геометрические модели — модели, представленные в виде объемных конструкций или графических форм.

Словесные модели — модели, выраженные устно или письменно.

Математические модели — модели, записанные с помощью уравнений, математических формул, неравенств, систем и т. п.

Структурные модели — схемы, графики, таблицы и т. п.

Логические модели — модели, в которых принимаются решения на основе анализа различных условий.

Специальные модели — ноты, химические формулы и т. п.

Компьютерные модели — модели, реализованные на компьютере с помощью программного обеспечения.

Формализация — процесс построения информационной модели.

Приведем общую классификацию основных видов моделирования:

· концептуальное моделирование– представление системы с помощью специальных знаков, символов, операций над ними или с помощью естественных или искусственных языков;

· физическое моделирование– моделируемый объект или процесс воспроизводится исходя из соотношения подобия, вытекающего из схожести физических процессов и явлений;

· структурно – функциональное моделирование – моделями являются схемы (графы, блок-схемы), графики, диаграммы, таблицы, рисунки со специальными правилами их объединения и преобразования;

· математическое (логико-математическое) моделирование– построение модели осуществляется средствами математики и логики;

· имитационное (программное) моделирование– в этом случае логико-математическая модель исследуемой системы представляет собой алгоритм функционирования системы, программно-реализуемый на компьютере.

Указанные виды моделирования могут применяться самостоятельно или одновременно, в некоторой комбинации (например, в имитационном моделировании используются практически все перечисленные виды моделирования или отдельные приемы). Так, например, имитационное моделирование включает в себя концептуальное (на ранних этапах формирования имитационной модели) и логико-математическое (включая методы искусственного интеллекта) моделирование для описания отдельных подсистем модели, а также в процедурах обработки и анализа результатов вычислительного эксперимента и принятия решений. Технология проведения и планирования вычислительного эксперимента с соответствующими математическими методами привнесена в имитационное моделирование из физического (экспериментального натурного или лабораторного) моделирования. Наконец, структурно-функциональное моделирование используется как при создании стратифицированного описания многомодельных комплексов, так и для формирования различных диаграммных представлений при создании имитационных моделей.

Понятие компьютерного моделирования трактуется шире традиционного понятия “моделирование на ЭВМ”. Приведем его.

 

Компьютерное моделирование

Методологией исследования СС является системный анализ. Один из важнейших инструментов прикладного системного анализа – компьютерное моделирование.
Имитационное моделирование является наиболее эффективным и универсальным вариантом компьютерного моделирования в области исследования и управления сложными системами.

Компьютерное моделирование– это метод решения задач анализа или синтеза сложной системы на основе использования ее компьютерной модели.

Компьютерное моделирование можно рассматривать как:

· математическое моделирование;

· имитационное моделирование;

· стохастическое моделирование.

Под термином “компьютерная модель” понимают условный образ объекта или некоторой системы объектов (или процессов), описанный с помощью уравнений, неравенств, логических соотношений, взаимосвязанных компьютерных таблиц, графов, диаграмм, графиков, рисунков, анимационных фрагментов, гипертекстов и т.д. и отображающих структуру и взаимосвязи между элементами объекта. Компьютерные модели, описанные с помощью уравнений, неравенств, логических соотношений, взаимосвязанных компьютерных таблиц, графов, диаграмм, графиков, будем называть математическими. Компьютерные модели, описанные с помощью взаимосвязанных компьютерных таблиц, графов, диаграмм, графиков, рисунков, анимационных фрагментов, гипертекстов и т.д. и отображающих структуру и взаимосвязи между элементами объекта, будем называть структурно-функциональными;

Компьютерные модели (отдельную программу, совокупность программ, программный комплекс), позволяющие, с помощью последовательности вычислений и графического отображения результатов ее работы, воспроизводить (имитировать) процессы функционирования объекта (системы объектов) при условии воздействия на объект различных, как правило, случайных факторов, будем называть имитационными.

Суть компьютерного моделирования заключена в получении количественных и качественных результатов на имеющейся модели. Качественные результаты анализа обнаруживают неизвестные ранее свойства сложной системы: ее структуру, динамику развития, устойчивость, целостность и др. Количественные выводы в основном носят характер анализа существующей СС или прогноза будущих значений некоторых переменных. Возможность получения не только качественных, но и количественных результатов составляет существенное отличие имитационного моделирования от структурно-функционального.

 

Методология компьютерного моделирования

Методологией компьютерного моделирования является системный анализ(направление кибернетики, общая теория систем), в котором доминирующая роль отводится системным аналитикам. В отличие от математического моделирования на ЭВМ, где методологической основой являются: исследование операций, теория математических моделей, теория принятия решений, теория игр и др.

Центральной процедурой системного анализа является построение обобщенной модели, отражающей все факторы и взаимосвязи реальной системы. Предметом компьютерного моделирования может быть любая сложная система, любой объект или процесс. Категории целей при этом могут быть самыми различными. Компьютерная модель должна отражать все свойства, основные факторы и взаимосвязи реальной сложной системы, критерии, ограничения.

Модель должна строиться целенаправленно.Целенаправленная модель представляет собой замену действительности с той степенью абстракции, которая необходима для поставленной цели. То есть, модель, прежде всего, должна отражать те существенные свойства и те стороны моделируемого объекта, которые определены задачей. При этом важно правильно обозначить и сформулировать проблему, четко определить цельисследования, проводимого с помощью моделирования.

Требования к моделям. Моделирование связано с решением реальных задач и необходимо быть уверенным, что результаты моделирования с достаточной степенью точности отражают истинное положение вещей, т.е. модель адекватна реальной действительности.

Хорошая модель должна удовлетворять некоторым общепринятым требованиям. Такая модель должна быть:

· адекватной;

· надежной;

· простой и понятной пользователю;

· целенаправленной;

· удобной в управлении и обращении;

· функционально полной с точки зрения возможностей решения главных задач;

· адаптивной, позволяющей легко переходить к другим модификациям или обновлять данные;

· допускающей изменения (в процессе эксплуатации она может усложняться).

В зависимости от целевой направленности модели, для нее задаются специальные требования. Наиболее характерными являются: целостность, отражение информационных свойств, многоуровневость, множественность (многомодельность), расширяемость, универсальность, осуществимость (реальная возможность построения самой модели и ее исследования), реализуемость (например, на ЭВМ, возможность материализации модели в виде реальной системы в задачах проектирования), эффективность (затраты временных, трудовых, материальных и других видов ресурсов на построение моделей и проведение экспериментов находятся в допустимых пределах или оправданы). Значимость или приоритетность требований к модели непосредственно вытекают из назначения модели. Например, в исследовательских задачах, задачах управления, планирования и описания важным требованием является адекватность модели объективной реальности. В задачах проектирования и синтеза уникальных систем важным требованием является реализуемость модели, например в САПР или систему поддержки принятия решений (СППР).

Цель моделирования и задание требований к модели определяют форму представления модели.

Любая модель (прежде чем стать объективно существующим предметом) должна существовать в мысленной форме, быть конструктивно разработанной, переведена в знаковую форму и материализована. Таким образом, можно выделить три формы представления моделей:

· мысленные (образы);

· знаковые (структурные схемы, описания в виде устного и письменного изложения, логические, математические, логико-математические конструкции);

· материальные (лабораторные и действующие макеты, опытные образцы).

Особое место в моделировании занимают знаковые, в частности логические, математические, логико-математические модели, а также модели, воссозданные на основе описания, составленного экспертами. Знаковые модели используются для моделирования разнообразных систем. Это направление связано с развитием вычислительных систем. Ограничимся ими в дальнейшем рассмотрении.

Следующий этап процедурной схемы – это выбор вида описания и
построения модели. Для знаковых форм такими описаниями могут быть:

· отношение и исчисление предикатов, семантические сети, фреймы, методы искусственного интеллекта и др. - для логических форм.

· алгебраические, дифференциальные, интегральные, интегрально-дифференциальные уравнения и др. - для математических форм.

Характер реализации знаковых моделей бывает:

· аналитический (например, система дифференциальных уравнений может быть решена математиком на листе бумаги);

· машинный (аналоговый или цифровой);

· физический (автоматный).

В каждом из них, в зависимости от сложности модели, цели моделирования, степени неопределенности характеристик модели, могут иметь место различные по характеру способы проведения исследований (экспериментов), т.е., методы исследования. Например, при аналитическом исследовании применяются различные математические методы. При физическом или натурном моделировании применяется экспериментальный метод исследования.

Анализ применяемых и перспективных методов машинного экспериментирования позволяет выделить расчетный, статистический, имитационный и самоорганизующийся методы исследований.

Расчетное (математическое) моделирование применяется при исследовании математических моделей и сводится к их машинной реализации при различных числовых исходных данных. Результаты этих реализаций (расчетов) выдаются в графической или табличной формах. Например, классической схемой является машинная реализация математической модели, представленной в виде системы дифференциальных уравнений, основанная на применении численных методов, с помощью которых математическая модель приводится к алгоритмическому виду, программно реализуется на ЭВМ, для получения результатов проводится расчет.