
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математические методы и экономика мобилизационного периодаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Постановка проблемы. Под мобилизационной экономикой будем понимать экономику, ресурсы которой сосредоточены в руках государства и используются для противодействия угрозам существования страны. Экономику мобилизационного периода мы рассмотрим применительно к России, против которой введены многочисленные политические и экономические санкции. Мобилизационная экономика необходима Новороссии (Донецкой и Луганской Народным Республикам), против которой Украина ведёт боевые действия и душит блокадой. Анализ последних достижений и публикаций. Наиболее полно принципы мобилизационной экономики изложены в трудах известных российских экономистов В.Ю.Катасонова [1] и С.Ю.Глазьева [2]. С прикладной точки зрения экономика мобилизационного периода – это сложная система. Основы моделирования таких систем разработаны в рамках математических методов исследования операций [3] и теории массового обслуживания [4]. Здесь должны быть упомянуты советские математики Б.В.Гнеденко, Е.С.Вентцель, Ю.В.Чуев, Н.П.Бусленко, И.Н.Коваленко и др. Плодотворно работают в области моделирования и прогнозирования российские математики В.А.Садовничий, А.А.Акаев, А.В.Каратаев, С.Ю.Малков и др. Формулировка нерешённых проблем. Затронутая тематика нуждается в детальной проработке экономических аспектов. Спектр математических методов, применяемых для моделирования экономик мобилизационного характера, нуждается в расширении. Цель работы. Предполагается дать обзор математических методов и моделей, которые могут быть полезными для мобилизационной экономики. Результаты исследования. По словам В.Ю.Катасонова, мобилизационная экономика «помогает любой стране, которая ведёт войну или готовится к ней, выиграть или хотя бы не проиграть». Такая экономика характеризуется высокой нормой накопления (объёмом инвестиций) в реальном производстве. По оценкам разных специалистов этот объём должен составлять от 30 до 40% ВВП. Мобилизационная экономика подразумевает максимальную защиту от внешних факторов. Государство должно иметь монополию на внешнюю торговлю и операции с валютой. Управление экономикой должно быть централизованным с большой долей государственных предприятий. Предпочтение отдаётся долгосрочному планированию в натуральных показателях. Такая экономика предполагает мобилизацию людей. Невозможно выиграть войну, не снижая потребления. Повышение уровня жизни – это, как правило, следствие победы и восстановительного периода. Переход на мобилизационную экономику является сложной задачей. Её нельзя решить, не подготовив человека, не объяснив ему, зачем нужна такая экономика. Надо убедить людей, что предстоит выбор между комфортом и самим существованием тебя, твоей семьи и твоей страны. Экономика мобилизационного периода направлена на укрепление обороноспособности страны. Поэтому в данной работе будет уделено большое внимание вопросам применения математических методов для описания и моделирования боевых действий. Из доступной советской литературы, пожалуй, лучшей книгой является [5]. Эта монография издана в 1969 г., но не утратила актуальности. В книге рассмотрены возможности количественной оценки конфликтных ситуаций, начиная от боёв дуэльного типа до сложных групповых столкновений при различных боевых порядках. Практические примеры демонстрируют область применения математических моделей. Простейшими являются математические модели комплексной оценки боевых средств воюющих сторон. Они приводят к оценке коэффициентов сопоставимости, позволяющих учитывать качество вооружения. Аналитические модели группового боя рассматривают как однородное, так и неоднородное расположение войск. В этих моделях используются равномерное, экспоненциальное и другие распределения вероятностей. Например, в [5, с. 92] предполагается, что время уничтожения цели в бою
где Дальнейшая формализация боевых действий рассматривается в виде задачи из теории массового обслуживания. Пусть имеется Требования поступают случайным образом с интенсивностью Такая постановка задачи приводит в итоге к определению вероятностей отказа в зоне обслуживания. Описаны методы определения основных параметров боевого процесса. Отдельно [5, гл. 5] описаны стохастические модели боевых действий. В них основную роль играют случайные функции времени – функция боеспособности, функция местоположения, функция скорости, функция характера действий, функция наличия боеприпасов. Тремя основными стохастическими моделями являются модель перемещения, модель обнаружения целей и модель стрельбы. Уделено внимание и компьютерному моделированию возможных ситуаций. Из доступной зарубежной литературы, по мнению автора тезисов, наиболее интересна книга [6]. Она посвящена построению математических моделей трудно формализуемых конфликтных ситуаций, не относящихся к стандартной теории игр и статистических решений. Математическим приложениям к военному делу уделено большое внимание в книге [7]. Здесь изложена теория дифференциальных игр – конфликтных ситуаций с бесконечным множеством альтернатив, поддающихся описанию дифференциальными уравнениями. Перейдём теперь к исследованиям наших современников. Простейшими эконометрическими методами исследуются законы истории, исторические макропроцессы, демография, экономика, войны в [8]. На отдельные очерки разбита книга [9]. Основное внимание уделяется гуманитарной интерпретации результатов математического и компьютерного моделирования. Академик С.Ю.Глазьев в своей фундаментальной работе [2] подробно разбирает экономическую, геополитическую и политическую обстановку в современном мире. Он объясняет американскую агрессию очередной сменой экономического уклада по теории циклов Кондратьева. Глазьев предлагает всеобъемлющую стратегию противостояния США и их союзникам. Примечательно, что академики А.А.Акаев и В.А.Садовничий в 2009 году предсказали нынешние события [10]. Новыми методами математического моделирования они спрогнозировали экстремальную точку падения экономической активности в 2014-16 гг. и связали с ней максимальный риск обострения политической напряжённости и схватку за лидерство. Выводы и предложения. В данной работе сделан обзор математических методов и моделей, пригодных для мобилизационной экономики. Такая экономика рассмотрена как сложная система. Наиболее подходящими признаны математические методы исследования операций, теория массового обслуживания, динамические модели на основе обыкновенных дифференциальных уравнений, эконометрические модели.
Литература:
1. Катасонов В.Ю. Бегство капитала из России: макроэкономический и валютно-финансовый аспекты: монография / В. Ю. Катасонов; МГИМО(У) МИД России, каф. междунар. валютно-кредитных отношений. – М.: МГИМО, 2002. – 164 с. – (Актуальные валютно-финансовые проблемы России). – ISBN 5-9228-0063-9. 2. Глазьев С.Ю. Как не проиграть в войне / С.Ю.Глазьев // Наш современник. – 2014. – №10. – С. 147-165. 3. Вентцель Е.С. Введение в исследование операций: учеб. пособ. / Е.С.Вентцель. – М.: Издательство «Советское радио», 1964. – 388 с.: ил., табл. – Библиогр.: с. 384. 4. Гнеденко Б.В., Коваленко И.Н. Введение теорию массового обслуживания: учеб. пособ. / Б.В.Гнеденко. – М.: Наука, 1966. – 432 с.: ил., табл. – Библиогр.: с. 421-428. 5. Ткаченко П.Н. Математические модели боевых действий: монография / П.Н.Ткаченко, Л.Н.Куцев, Г.А.Мещеряков, А.М.Чавкин, А.Д.Чебыкин; под ред. П.Н.Ткаченко. – М.: Издательство «Советское радио», 1969. – 240 с.: ил., табл. – Библиогр.: с. 235-236. 6. Саати Т.Л. Математические модели конфликтных ситуаций: монография / Т.Л.Саати. – М.: Издательство «Советское радио», 1977. – 304 с.: ил., табл. – Библиогр.: с. 291-296. 7. Айзекс Р. Дифференциальные игры: монография / Р.Айзекс. – М.: Издательство «Мир», 1967. – 479 с.: ил., табл. – Библиогр.: с. 455-456. 8. Коротаев А.В. Законы истории. Математическое моделирование исторических макропроцессов. Демография, экономика, войны: монография / А.В.Коротаев, А.С.Малков, Д.А.Халтурина. – М.: КомКнига, 2005. – 344 с.: ил., табл. – Библиогр.: с. 328-343. – ISBN 5-484-00029-7. 9. Белотелов Н.В. Законы истории. Математическое моделирование. Гуманитарный анализ: Исследование исторических, военных, социально-экономических и политических процессов: монография / Н.В.Белотелов, Ю.И.Бродский, Ю.Н.Павловский. – М.: Книжный дом «ЛИБРОКОМ», 2009. – 320 с.: ил., табл. – Библиогр.: с. 314-318. – ISBN 978-5-397-00659-0. 10. Садовничий В.А. Моделирование и прогнозирование мировой динамики: монография / В.А.Садовничий, А.А.Акаев, А.В.Каратаев, С.Ю.Малков. – М.: ИСПИ РАН, 2012. – 359 с.: ил., табл. – Библиогр.: с. 334-353. – ISBN 978-5-7556-0456-7.
Скрыпник Т.М. Донецкий национальный университет
|
||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 431; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.140.232 (0.009 с.) |

 является случайной величиной, подчинённой экспоненциальному закону с функцией распределения вероятностей:
является случайной величиной, подчинённой экспоненциальному закону с функцией распределения вероятностей: ,
, – это среднее число целей, уничтоженных в единицу времени одним боевым средством.
– это среднее число целей, уничтоженных в единицу времени одним боевым средством. однотипных устройств (танков), предназначенных для обслуживания потока требований. Считают, что продолжительность обслуживания каждого требования подчиняется экспоненциальному закону
однотипных устройств (танков), предназначенных для обслуживания потока требований. Считают, что продолжительность обслуживания каждого требования подчиняется экспоненциальному закону  . Только теперь
. Только теперь 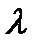 , характеризуемой математическим ожиданием числа требований в единицу времени. Если свободно хотя бы одно устройство, то поступившее требование обслуживается. Если все устройства заняты, то требования направляются в очередь на обслуживание.
, характеризуемой математическим ожиданием числа требований в единицу времени. Если свободно хотя бы одно устройство, то поступившее требование обслуживается. Если все устройства заняты, то требования направляются в очередь на обслуживание.


