
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоретико-игровые подходы в экономикеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение проблемы. На практике часто возникает необходимость согласования действий экономических субъектов в случаях, когда их интересы не совпадают. В таких ситуациях теория игр позволяет найти лучшее решение для поведения участников при столкновении интересов. Актуальность. Изучение теории игр является обязательным для современного экономиста, т.к. выбор оптимальной стратегии поведения максимизирует прибыль, что в свою очередь является одной из главных целей экономической деятельности. Анализ последних достижений и публикаций. Достижения в области теории игр отмечены большим количеством Нобелевских премий по экономике. В 2005 г. премию получили Томас Шеллинг, работы которого стали фундаментом современного стратегического анализа во внешней политике и в бизнесе, и Роберт Ауманн, подчеркнувший роль представлений игроков о том, что думают другие игроки. В 2007 – Леонид Гурвиц, придавший точный математический смысл идее о том, что в плановой экономике невозможно создать правильные стимулы для экономических субъектов, Эрик Маскин и Роджер Майерсон, сформулировавшие общую задачу создания правильных стимулов и создавшие важную часть экономической теории последних десятилетий – теорию аукционов [1]. Жан Тироль – лауреат 2014 года – использовал теоретико-игровые подходы в анализе рыночной власти и её регулирования [2]. Целью работы является дать общее представление о строгих методах, используемых для анализа широкого класса конфликтных взаимодействий в экономике. На практическом примере планируется сделать постановку игровой задачи и найти её оптимальные решения. Основная часть. Рассмотрим наиболее классические задачи теории игр. Для начала стоит определиться с понятиями. Игра представляет собой математическую модель реальной конфликтной ситуации, анализ которой ведется по определенным правилам. Стороны, участвующие в игре (конфликте), называются игроками. Стратегией игрока называется совокупность правил, определяющих выбор варианта действия при каждом личном ходе игрока в зависимости от ситуации, сложившейся в процессе игры. Стратегия называется оптимальной, если она обеспечивает данному игроку при многократном повторении игры максимально возможный средний выигрыш или минимально возможный средний проигрыш независимо от поведения противника. Рассмотрим конечную игру двух лиц (I и II) с нулевой суммой (выигрыши двух игроков противоположны). Такую игру удобно описать в виде платежной матрицы(табл. 1). Предположим, что игрок I имеет m стратегий (обозначим их 1, 2, … m), аналогично игрок II имеет n стратегий, Предполагается, что игроки действуют рационально, и каждый из них делает все, чтоб выбрать для себя наилучшую стратегию. Это означает, что при выборе стратегии игрока I мы должны учитывать, что игрок II ответит на нее той стратегией, которая минимизирует выигрыш игрока I. Поэтому найдем минимальное Зная все Величина Таблица. 1 Платежная матрица
Игрок II будет пытаться минимизировать выигрыш игрока I, поэтому необходимо в каждом из столбцов найти максимальное значение
Если В играх без селовых точек решение сводится к поиску смешанных стратегий, т.е. частот применения каждой из чистых стратегий. Смешанные стратегии для каждого из игроков обозначим Решение подобной задачи сводится к решению двойственной задачи линейного программирования (табл. 2). Таблица. 2 Двойственная пара задач линейного программирования
В табл. 2 используются следующие обозначения: Особый интерес представляют игры с природой (социально-экономической средой). Природа является одним из игроков, но она не может выбирать для себя оптимальные стратегии и действует случайным образом, что представляет определенную сложность для разумного игрока при выборе оптимальной стратегии. Существует несколько методов решения задач с природой. Если вероятности состояний природы В условиях полной неопределенности используют максиминный критерий Вальда (критерий крайнего пессимизма), критерий минимаксного риска Сэвиджа а также критерий Гурвица [3, с. 287-312]. Для наглядности рассмотрим задачу игры с природой [3, с. 321]. Необходимо определить, какую электростанцию построить в одном из районов страны, чтобы эффективность использования капиталовложений была наибольшей при самых неблагоприятных условиях. Планирующий орган имеет три стратегии использования капиталовложений: А1 - вложить средства в ГЭС, А2 – в ТЭС, А3 – в АЭС. Случайные факторы, влияющие на экономическую эффективность, применяемых плановым органом стратегий, можно рассматривать как состояния природы (П1, П2), где П1 – благоприятное состояние, П2 – не благоприятное состояние. Экономический эффект (млн ден. ед.) трёх стратегий планового органа оценен с учётом затрат на строительство и издержек в процессе эксплуатации, зависящих от состояния природы, и представлен в табл. 3. Таблица. 3 Экономический эффект стратегий
Решив задачу максиминным критерием Вальда, получим Подведение итогов. Мы исследовали базовые теоретико-игровые подходы к решению конфликтов в экономике, научились находить оптимальные стратегии. Придали практическое значение нашему исследованию, решив задачу игры с природой, в которой нашли оптимальные стратегии для использования капиталовложений.
Литература: 1. 10 фактов о теории игр [Электронный ресурс]. – Режим доступа: http://trv-science.ru/2011/08/16/10-faktov-o-teorii-igr/ 2. Уроки стратегии от нобелевского лауреата по экономике Жана Тироля [Электронный ресурс]. – Режим доступа: http://hbr-russia.ru/upravlenie/strategiya/p14741/ 3. Костевич Л.С. Математическое программирование: информационные технологии оптимальных решений: [учеб. пособие] / Л.С.Костевич. – Мн.: Новое знание, 2003. – 424 с.: ил. – Библиогр.: с. 419. – ISBN 985-6516-83-8. 4. Полшков Ю.Н. Теоретико-игровые подходы в математическом моделировании международной торговли // Проблемы развития внешнеэкономических связей и привлечения иностранных инвестиций: региональный аспект. Сборник научных трудов. – Донецк: ДонНУ. – 2012. – Т. 1. – С. 309-314.
Билан А.С. Полшков Ю.Н. Донецкий национальный университет
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 578; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.007 с.) |

 – выигрыш игрока I (
– выигрыш игрока I (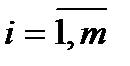 ;
;  ).
).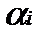
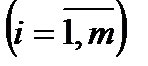 и запишем рядом с платежной матрицей (табл. 1) добавочный столбец:
и запишем рядом с платежной матрицей (табл. 1) добавочный столбец: 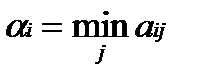 ,
, 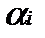 , игрок I должен предпочесть другим стратегиям ту, для которой
, игрок I должен предпочесть другим стратегиям ту, для которой 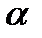 , получим:
, получим: .
.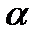 называется нижней ценой игры (максимином). Это гарантированный выигрыш, который может обеспечить себе игрок I.
называется нижней ценой игры (максимином). Это гарантированный выигрыш, который может обеспечить себе игрок I.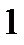
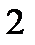
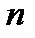
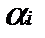
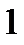
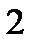 …
…
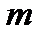
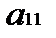
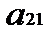 …
…


 …
…
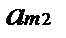
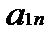
 …
…
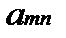
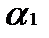
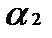 …
…
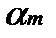

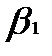
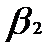
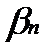
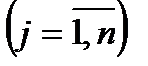 и среди этих значений выбрать наименьшее
и среди этих значений выбрать наименьшее 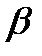 . Полученная величина
. Полученная величина 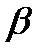 – верхняя цена игры (минимакс):
– верхняя цена игры (минимакс):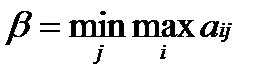 .
.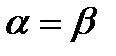 , то игру называют игрой с седловой точкой, а эта точка определяет оптимальные чистые стратегии
, то игру называют игрой с седловой точкой, а эта точка определяет оптимальные чистые стратегии 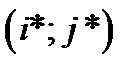 для каждого из игроков и чистую цену игры
для каждого из игроков и чистую цену игры 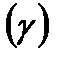 , которые и являются решением игры.
, которые и являются решением игры.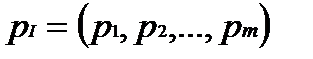 и
и  , где
, где  ,– вероятности применения чистых стратегий
,– вероятности применения чистых стратегий  и
и  , при этом
, при этом 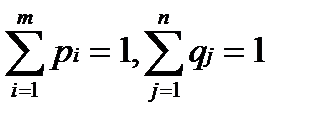 . Выигрыш, полученный в результате применения этих стратегий, равен цене игры
. Выигрыш, полученный в результате применения этих стратегий, равен цене игры 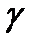 .
.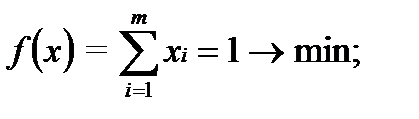
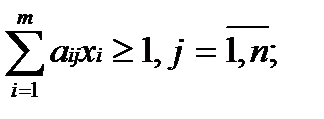
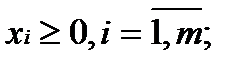
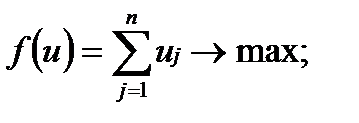

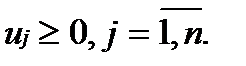
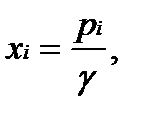
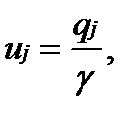
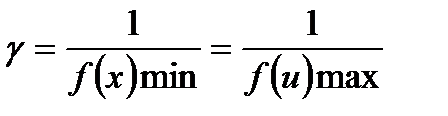 .
.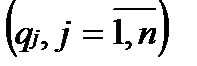 известны или могут быть оценены субъективно, то
известны или могут быть оценены субъективно, то 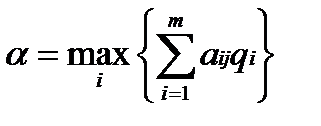 . При этом оптимальная стратегия соответствует максимальному среднему значению выигрыша.
. При этом оптимальная стратегия соответствует максимальному среднему значению выигрыша.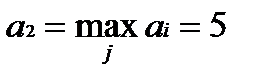 млн ден. ед., то есть А2 – оптимальная стратегия, которая обеспечит наибольшую эффективность капиталовложений при самых неблагоприятных условиях. Эту задачу можно так же решить с учетом того, что природа действует разумно, согласно методу, описанному в [4], тогда задача сведется к поиску смешанных стратегий. В ответе получим оптимальную смешанную стратегию для первого игрока
млн ден. ед., то есть А2 – оптимальная стратегия, которая обеспечит наибольшую эффективность капиталовложений при самых неблагоприятных условиях. Эту задачу можно так же решить с учетом того, что природа действует разумно, согласно методу, описанному в [4], тогда задача сведется к поиску смешанных стратегий. В ответе получим оптимальную смешанную стратегию для первого игрока 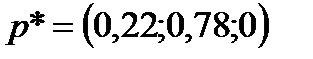 , для второго
, для второго 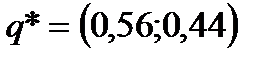 и цену игры
и цену игры 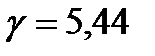 млн ден. ед.
млн ден. ед.


