
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы параметрического программирования в задачах оптимального выпуска продукцииСодержание книги
Поиск на нашем сайте
Постановка проблемы. Во многих оптимизационных задачах исходные данные зависят от некоторого параметра. Такие задачи называются задачами параметрического программирования. Актуальность данной работы обусловлена тем, что параметрическое программирование позволяет приблизить к реальности условия задач линейной оптимизации. Например, если коэффициенты целевой функции представляют собой цены некоторых продуктов, то можно предположить, что эти цены не постоянны, а являются функциями параметра времени. Целью исследования является описание методов определения интервала значений того или иного параметра, в пределах которого решение остается оптимальным. Практическое применение параметрического программирования будет осуществлено на примере задачи оптимального выпуска продукции. Анализ достижений и публикаций. Первые работы по параметрическому программированию были опубликованы в 1955 году американскими математиками Гассом и Саати. Среди первых советских учёных, занимавшихся параметрическим программированием, стоит упомянуть Карабегова, чья статья вышла в 1963 году в «Журнале вычислительной математики и математической физики». Первое учебное пособие по данной проблематике напечатали в 1966 году советские математики Гольштейн и Юдин. Основные публикации по параметрическому программированию перечислены в библиографии книги [1]. Данный раздел линейного программирования хорошо изложен в [2, с. 162-172], [3, с. 360-366]. Основная часть. Задачи параметрического программирования являются обобщением задач линейной оптимизации. Это обобщение состоит в том, что данные в задаче линейной оптимизации считают не постоянными величинами, а функциями, определённым образом зависящих от некоторых параметров. Пусть коэффициенты целевой функции зависят от числового параметра
при условиях
Остановимся на геометрической интерпретации данной задачи. Если система ограничений совместна, и являет собой выпуклый многогранник, то уравнению Опишем алгоритм решения задачи параметрического программирования при помощи графического метода: 1) определяем ОДР системы ограничений; 2) для получения функции с постоянными коэффициентами придаём значение Этапы аналитического решения задачи параметрического программирования приведены в учебном пособии [2, с. 166-171]. Приведём пример графического решения. Сельскохозяйственное предприятие выращивает фрукты поздних сортов (груши и яблоки). Фрукты могут быть реализованы сразу или заложены для хранения с последующей реализацией по более высокой цене. Прогнозируемая прибыль от реализации 1т фруктов с течением времени изменяется и выражается следующими зависимостями: Требуется определить, сколько фруктов каждого вида заложить на хранение, чтобы получить максимум прибыли от реализации продукции. Известно, что вместимость склада 250 т, а груш можно заложить на хранение не более 60 т. Трудовые ресурсы предприятия ограниченны и составляет 200 человеко-месяцев, а затраты труда на хранение и реализацию 1 т фруктов равны соответственно 0,7 и 0,47 человеко-месяца. Математическая модель задачи имеет вид:
Придадим параметру Приравняем
Запишем угловой коэффициент
Его начальное значение при
Очевидно, что при любом
При
Итак, при Поэтому сельскохозяйственному предприятию можно порекомендовать не оставлять груши на хранение. На хранение следует оставить 250 т яблок. После семи месяцев хранения продать их и получить прибыль 1300 ден.ед. Подведение итогов. В данном исследовании проведен анализ решения задач параметрического программирования, рассмотрен графический метод и упомянут аналитический. Выделены основные черты и алгоритм решения. Обстоятельно рассмотрены все этапы решения задачи оптимального выпуска продукции в зависимости от значения параметра. Таким образом, можно сделать вывод о том, что задачи параметрического программирования являются обобщением задач линейной оптимизации. Решая такие задачи, мы можем наиболее точно определить значение целевой функции, которая часто зависит от многих параметров.
Литература: 1. Гольштейн Е.Г. Новые направления в линейном программировании: [учеб. пособие] / Е.Г.Гольштейн, Д.Б.Юдин. – М.: Советское радио, 1966. – 525 с.: ил. – Библиогр.: с. 516-520. 2. Костевич Л.С. Математическое программирование: информационные технологии оптимальных решений: [учеб. пособие] / Л.С.Костевич. – Мн.: Новое знание, 2003. – 424 с.: ил. – Библиогр.: с. 419. – ISBN 985-6516-83-8. 3. Таха Х.А. Введение в исследование операций, 7-е издание.: Пер. с англ. / Х.А.Таха. – М.: Издательский дом «Вильямс», 2005. – 912 с.: ил. – ISBN 5-8459-0740-3 (рус.).
|
||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 879; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.011 с.) |

 , который изменяется в некоторых пределах, т.е.
, который изменяется в некоторых пределах, т.е.  . Для каждого значения параметра нужно найти свой оптимальный план
. Для каждого значения параметра нужно найти свой оптимальный план  , максимизирующий целевую функцию
, максимизирующий целевую функцию ,
,

 соответствует семейство гиперплоскостей, проходящих через начало координат. Вследствие придания параметру
соответствует семейство гиперплоскостей, проходящих через начало координат. Вследствие придания параметру  конкретных числовых значений, гиперплоскость
конкретных числовых значений, гиперплоскость 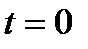 ; 3) приравниваем
; 3) приравниваем  этой прямой и исследуем его поведение при изменении параметра
этой прямой и исследуем его поведение при изменении параметра  ден.ед. для груш и
ден.ед. для груш и  ден.ед. для яблок, где
ден.ед. для яблок, где  .
.


 . Максимальное значение прибыли 443 ден.ед. достигается в вершине В(60;190).
. Максимальное значение прибыли 443 ден.ед. достигается в вершине В(60;190). к нулю и найдём уравнение целевой прямой при любом
к нулю и найдём уравнение целевой прямой при любом  .
. этой прямой и исследуем его поведение при изменяющемся параметре
этой прямой и исследуем его поведение при изменяющемся параметре 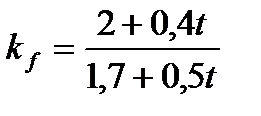 .
. . Найдем производную углового коэффициента по параметру
. Найдем производную углового коэффициента по параметру  .
. . Найдём предел его возрастания:
. Найдём предел его возрастания: .
. , значение
, значение  приближается к –0,8 со стороны отрицательных значений. Целевая прямая поворачивается против часовой стрелки, до предельного положения
приближается к –0,8 со стороны отрицательных значений. Целевая прямая поворачивается против часовой стрелки, до предельного положения  . В рассматриваемом примере при изменении параметра
. В рассматриваемом примере при изменении параметра 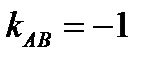 . Следовательно,
. Следовательно, ,
, 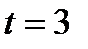 .
. оптимальное решение задачи будет в вершине В(60;190) и максимальная прибыль будет колебаться от 443 до 800 ден.ед. При
оптимальное решение задачи будет в вершине В(60;190) и максимальная прибыль будет колебаться от 443 до 800 ден.ед. При  оптимальное решение будет в точке А(0;250) и максимальная прибыль может изменяться от 800 до 1300 ден.ед.
оптимальное решение будет в точке А(0;250) и максимальная прибыль может изменяться от 800 до 1300 ден.ед.


