
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
On a mathematical model of the state economy with elements of Stochastic ProcessesСодержание книги
Поиск на нашем сайте
Formulation of the problem. The need for the international division of labor, the exchange of goods, services, and scientific and technological achievements due to divergence of natural, economic, technological, scientific indicators and historical traditions. Issues of this work is the application of mathematical methods to the modeling of the behavior of the state economy. Analysis of recent achievements and publications. In their studies, we rely on a mathematical model of an open economy, which consists of three sectors. This model is designed by a famous Russian economist V. A. Kolemaev. We will use the results of the author of this thesis in the field of financial mathematics [1], the optimal control [2] and stochastic estimation [3]. The wording of unsolved problems. It is planned to justify the need for random processes in the proposed model of the state economy. Is expected to receive the findings of the benefits or, conversely, inappropriate international trade, about the range of products and sales. The purpose of the work. It is planned to develop a mathematical model of the state economy, adapted to the practical needs. It is supposed to reveal the qualitative dependence, reflecting the impact of foreign economic activity for the state economy. The results of the study. We describe a model that will be the foundation for us. It is expected that the national economy is divided into three sectors: the material (zero, number Let through Technological structure remains unchanged and is given by linear-homogeneous neoclassical production functions (Cobb – Douglas functions):
The total of workers
Labor sector balance is written as:
We also believe that the delay investments insignificant coefficients depreciation
where In the presence of foreign trade, a credit balance of the investment has a term
The expenditure part of the material balance contains a term
Along with our own production of consumer goods
where With all the advantages of the model (1) - (7) it does not take into account the factor of randomness, a very significant during the global economic crisis. According to the author of this work the main "chance" lies in the dynamics of fixed assets (4). We write the differential equation (4) as follows:
The value of gross investment
where This approach allows us to use significant theoretical results obtained by famous Donetsk mathematician B. V. Bondarev and his followers [1]. Author abstracts made a personal contribution to the development of this subject [2-3]. Equation (4) will receive the form:
It will be written as:
Given the Cauchy obtain
where
At sufficiently broad assumptions sequence Model (1) - (7) in view of (4*) implies such an ideological sense. Under the possibility of foreign trade we mean the ability to carry out the national economy equivalent exchange of raw materials, energy and other materials on foreign investment and consumer goods. Under the feasibility of foreign trade will gain understanding of the industrial development of the country while maintaining or increasing the proportion of consumption. The unfolding global economic crisis enhances autarky in the world market. Under autarky in the economy as the creation of a closed economy within a country or union of states, leading to the disruption of traditional economic international relations. We live in an era of globalization, when all countries are closely related to the system of international economic relations. Therefore, we will talk about the autarkic tendencies arising from the intensification of the contradictions associated with the global economic crisis. Such trends are most powerfully manifested themselves during the global economic crisis of 1929-1933. Then there was a gap of pre-existing trade and other economic relations. States pursued a policy of "beggar my neighbor". This is clearly illustrated by the political and economic decisions of the United States and its allies. Introduced sanctions against Russia solved several problems. These objectives are to strengthen the prevention of Russia, the weakening of the European Economic Union (competitor of the United States of America), intimidation of China, India and other growing economies, full control over weak states (Ukraine, Georgia, Moldova), etc. Conclusions and suggestions. The developed mathematical model covers the main components of the national economy: technological structure, the dynamics of employment and the distribution of funds, labor, investment, material and trade balance. The model uses elements of stochastic processes. The prospects of the economy during the global crisis. Qualitative dependence, reflecting the impact of foreign economic activity for the state economy. References:
1. Bondarev B.V., Polshkov Yu.N. On the some problem of R. Merton // Theory of Stochastic Processes. – 1997. – V. 3 (19), N. 1-2. – P. 132-140. 2. Polshkov Yu.N. On an estimate of the convergence rate // Theory of Stochastic Processes. – 2000. – V. 6 (22), N. 1-2. – P. 116-124. 3. Polshkov Yu.N. Quasi-maximal likelihood estimator of the unknown parameter in systems with “physical” white noise // Random Operators and Stochastic Equations. – 2001. – V. 9, N 3. – P. 263-274.
Абраменко С. В. Полшков Ю. Н. Донецкий национальный университет
|
||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 414; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.201.93 (0.007 с.) |

 ) sector produces objects of labor; sector to establish a fund (first, number
) sector produces objects of labor; sector to establish a fund (first, number  ) produces a means of labor; consumer (second, number
) produces a means of labor; consumer (second, number  ) sector produces commodities. For each sector of fixed production assets. Work and investment can move freely between sectors.
) sector produces commodities. For each sector of fixed production assets. Work and investment can move freely between sectors. designated volume of output in the sector
designated volume of output in the sector  ,
,  . Accordingly,
. Accordingly,  is the cost of fixed assets,
is the cost of fixed assets,  is the quantity of workers in the industrial sector.
is the quantity of workers in the industrial sector. . (1)
. (1) has a constant growth rate
has a constant growth rate 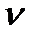 . Allowed the continuity of time
. Allowed the continuity of time  , which is used exponential dependence:
, which is used exponential dependence: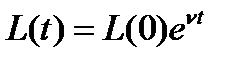 . (2)
. (2) . (3)
. (3) of fixed assets and the coefficients of direct costs
of fixed assets and the coefficients of direct costs  for materials sectors are permanent. Consequently, the change for the year of fixed assets for the sector
for materials sectors are permanent. Consequently, the change for the year of fixed assets for the sector  is made up of depreciation (
is made up of depreciation ( ) and gross investment (
) and gross investment ( ). The dynamics of fixed assets is defined by ordinary differential equations:
). The dynamics of fixed assets is defined by ordinary differential equations: , (4)
, (4) .
. that describes the import of capital goods. The balance will look like this:
that describes the import of capital goods. The balance will look like this: . (5)
. (5) that refers to the export of materials. Material balance is:
that refers to the export of materials. Material balance is: . (6)
. (6) , has their import
, has their import  . The trade balance is as follows:
. The trade balance is as follows: , (7)
, (7) ,
,  ,
,  are the world prices for the products of the material, to create a fund and consumer sectors.
are the world prices for the products of the material, to create a fund and consumer sectors. .
. depend on the value of fixed assets
depend on the value of fixed assets  . Assume that these parameters are related by:
. Assume that these parameters are related by: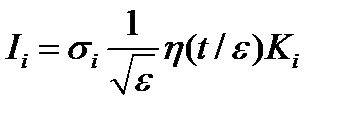 ,
, is the coefficient of variation (volatility) of each of the sectors,
is the coefficient of variation (volatility) of each of the sectors,  ;
;  is a small positive parameter;
is a small positive parameter;  is a certain stationary random process with zero mean, which satisfies one of the conditions of the weak dependence.
is a certain stationary random process with zero mean, which satisfies one of the conditions of the weak dependence. .
.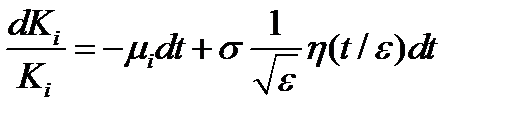 . (4*)
. (4*) ,
, .
. when
when  converges weakly to a standard Wiener process
converges weakly to a standard Wiener process 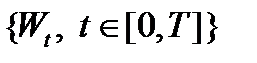 . Perturbations generated by a random process
. Perturbations generated by a random process  , called "physical" white noise. He turns to white noise only in the limit. Up to the limit can be reasonably strong correlation between disturbances in the intimate moments of time.
, called "physical" white noise. He turns to white noise only in the limit. Up to the limit can be reasonably strong correlation between disturbances in the intimate moments of time.


