О развитии модели спроса и предложения в курсе математики для экономистов
Похожие статьи вашей тематики
В настоящее время математические методы все более используются в экономике для анализа и моделирования. Обучение тому, как преобразовать важные аспекты экономической проблемы в абстрактную, упрощенную экономическую модель – это часть образования экономиста. Построение новой обоснованной модели конкретного экономического процесса или явления является сложной задачей. Поэтому при изложении курса «Математика для экономистов» важно рассматривать, как строить и развивать хорошо известные модели, обоснованность которых не подвергается сомнению.
Способам такого изложения уделяли и уделяют внимание многие авторы, например, [1], [2]. Развитию математических методов моделирования экономики посвящен ряд монографий и учебников [3], [4] и др., в которых рассматриваются прикладные аспекты методов математического моделирования к различным экономическим процессам и явлениям
На примере модели Вальраса регулирования цены проиллюстрируем, как эта модель развивается, усложняется, уточняется в курсе математики для экономистов.
Простейшую линейную зависимость спроса и предложения от цены товара мы рассматриваем уже в разделе «Аналитическая геометрия»

где p-цена товара, d-спрос, s-предложение; 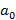 , ,  , , 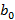 , ,  -некоторые числовые параметры. -некоторые числовые параметры.
Анализируя эту модель, можно определить точку рыночного равновесия, изучить влияние на нее введения дополнительного налога или субсидии.
Далее к этой же модели можно вернуться в разделе «Линейная алгебра» при изучении темы «Системы линейных алгебраических уравнений», рассмотрев равновесие спроса и предложения для нескольких рынков.
Поскольку многие экономические процессы динамические по своей сути, то при изложении раздела «Дифференциальные уравнения первого порядка» от статической модели переходим к динамической


где p’(t) характеризует тенденцию изменения цены.
Отсюда получаем дифференциальное уравнение первого порядка

для нахождения цены p(t).
Решая это дифференциальное уравнение, получаем

где 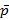 - равновесная цена, - равновесная цена,  . .
Изучение вида найденного решения показывает, как стабилизация цены зависит от значения параметров  и и  . .
Развитие этой же модели продолжается при изучении дифференциальных уравнений второго порядка с постоянными коэффициентами, где учитывается влияние на рыночную цену равновесия остатков нереализованного товара. Эта проблема может быть математически выражена следующим уравнением

Как и прежде, предполагается линейная зависимость

Эта модель регулирования цены может быть приведена к дифференциальному уравнению второго порядка

Анализ решения уравнения показывает, что в зависимости от его параметров изменение цены от начальной до равновесной может иметь либо монотонный, либо колебательный характер.
Другая разновидность динамической модели спроса и предложения, так называемая «паутинная модель», рассматривается при изучении линейных разностных уравнений.
Пусть функции предложения и спроса имеют вид
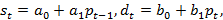
где  - предложение, спрос и рыночная цена в момент времени t. - предложение, спрос и рыночная цена в момент времени t.
Тогда соответствующее разностное уравнение получаем в виде

Его решением является функция

где 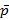 - точка равновесия цены. - точка равновесия цены.
Если  , то цена сходится к точке равновесия. Само же разностное уравнение позволяет определить цену товара в последующий период времени в зависимости от предыдущей цены и параметров, входящих в функции , то цена сходится к точке равновесия. Само же разностное уравнение позволяет определить цену товара в последующий период времени в зависимости от предыдущей цены и параметров, входящих в функции 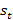 и и  . .
При подобном рассмотрении этой и других экономико-математических моделей студенты-экономисты учатся, как использовать в своей профессиональной и исследовательской деятельности логический подход к изучаемому явлению, проводить анализ полученных решений.
Литература:
1. Агапова Т.М., Бехренс Д., Курран Д. Динамические системы в экономике / Т.М.Агапова. – Донецк: ДонГУ, 2000. – 140 с.
2. Гончаренко Я.В. Экономико-математические методы и модели в системе подготовки студентов экономических специальностей / Я.В.Гончаренко // Дидактика математики: проблеми і дослідження.- Вип.36. – Донецьк: ДонНУ,2011.- С.48-53
3. Колемаев В.А. Математическая экономика: уч. для вузов / В.А.Колемаев.- М.: ЮНИТИ, 1998.- 240с.
4. Нельсон Р., Уинтер С. Эволюционная теория экономических изменений / Р.Нельсон, С.Уинтер.- М.:ЗАО «Финстатинформ», 2000.- 474с.
Цыбульник А.С.
Полшков Ю.Н.
Донецкий национальный университет
|