
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение цепей маркова для моделирования процесса занятости населенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В настоящее время в Украине наблюдается рост безработицы, в котором отражаются острейшие противоречия современного состояния экономики, углубление общего кризиса. Это обусловлено переплетением структурных кризисов – политическим, энергетическим, сырьевым, валютно-финансовым, - инфляцией, замедлением темпов экономического развития. В комплексе мер по повышению прибыльности производства, применяемых предприятиями, возрастает роль экономии на рабочей силе и в первую очередь за счет сокращения численности персонала. На многих предприятиях практикуется «выдавливание» работников: человеку сокращают число рабочих часов и платят соответствующую заработную плату, на которую очень трудно прожить. Поэтому многие начинают искать новое место работы. В программах правительства Украины на ближайшие годы проблема занятости остается второстепенной. При этом незанятость части трудоспособного населения приводит к издержкам в виде потерь реально возможного, но упущенного валового внутреннего продукта. Теоретическим и практическим вопросам изучения функционирования рынков труда посвящены работы отечественных и зарубежных авторов: Мортикова, Бидюка, Хейне и др. Целью данной работы является построение модели процесса занятости населения с помощью конечных цепей Маркова. Исследование такого процесса приводит к системе разностных уравнений. При моделировании рассматривается перемещение временно незанятых из-за отсутствия работы между двумя состояниями: безработицы и новой занятости. Пусть на некотором рынке труда в момент времени Таким образом, для первоначально уволенных работников (обозначим их количество через n) начинается цепь событий. В течение каждого периода после начального увольнения происходит перемещение некоторого количества людей из состояния безработных в состояния нанятых на работу, и наоборот, перемещение некоторого количества людей из состояния работающих в состояния безработных. Предположим, что m из n уволенных работников нашли работу сразу же, то есть в начальный момент времени t=0 имеется (n-m) безработных и m работающих. Тогда в период t=1 найдут работу и работающих
Отметим, что в каждый период времени количество безработных и работающих изменяется. Далее наша задача состоит в том, чтобы установить, будет ли этот процесс сходиться к устойчивому состоянию. Предположим, что часть (вероятность) занятых работников в период t равна
Аналогично, часть безработных в период (t+1) состоит из той части, которая была безработной и осталась безработной (она составляет (1-
Это однородная система линейных разностных уравнений описывает, как вероятности занятости и незанятости работников изменяются от предыдущего периода к последующему. В матричной форме она имеет вид
Решение системы ищем в виде
где
Решая это уравнение, получаем Собственные векторы, соответствующие найденным собственным значениям матрицы А, находим из системы уравнений
В результате получаем два частных решения
и общее решение как их линейную комбинацию
Постоянные
Найденное решение позволяет определить траекторию вероятностей занятого населения и безработных с течением времени. Так как Отсюда можно сделать вывод, что хотя перемещения людей между двумя группами работающих и безработных будут продолжаться, но пропорциональное соотношение между этими группами будет характеризоваться этими значениями. Данная модель является макроэкономической и в качестве объекта моделирования может быть выбран рынок труда любой территориальной единицы.
Литература: 1. Кемени Дж., Снелл Дж. Конечные цепи Маркова / Дж. Кемени, Дж. Снилл.- М:Наука, 1970.-272с.
Скрыпник Т.М., Новожилова Е.Г. Донецкий национальный университет
|
||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 440; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.68.39 (0.009 с.) |

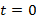 произошли структурные изменения вследствие увольнения работников, причиной которого стало сокращение объемов производства. Допустим, что только малая их часть может найти работу немедленно. Обозначим эту часть
произошли структурные изменения вследствие увольнения работников, причиной которого стало сокращение объемов производства. Допустим, что только малая их часть может найти работу немедленно. Обозначим эту часть  . Оставшаяся часть, став безработной, ищет другую работу. Обозначим эту часть
. Оставшаяся часть, став безработной, ищет другую работу. Обозначим эту часть  ,
,  . Пусть вероятность найти работу в течение некоторого периода времени t равна
. Пусть вероятность найти работу в течение некоторого периода времени t равна  , то есть, в среднем, можно ожидать, что часть
, то есть, в среднем, можно ожидать, что часть 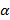 , то есть, в среднем, можно предполагать, что часть
, то есть, в среднем, можно предполагать, что часть 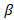 )(n-m) останутся безработными. Далее, принимая во внимание то, что вероятность потерять работу для тех, кто её имел, равна
)(n-m) останутся безработными. Далее, принимая во внимание то, что вероятность потерять работу для тех, кто её имел, равна 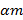 (из нашедших работу немедленно) станут безработными, а
(из нашедших работу немедленно) станут безработными, а  сохранят её. Таким образом, к концу первого периода имеется в сумме
сохранят её. Таким образом, к концу первого периода имеется в сумме 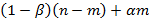 безработных и
безработных и 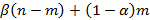 работающих. Аналогично, в течение периода t=2 найдут работу
работающих. Аналогично, в течение периода t=2 найдут работу  , а
, а  останутся безработными. Из тех же, которые были наняты, станут незанятыми
останутся безработными. Из тех же, которые были наняты, станут незанятыми  и
и  сохранят работу. И в сумме к концу второго периода имеем количество безработных
сохранят работу. И в сумме к концу второго периода имеем количество безработных 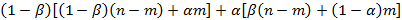
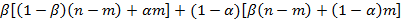 и т.д.
и т.д.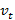 , а незанятых
, а незанятых 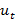 . Часть занятых в период (t+1) состоит из той части, которая имела работу в предыдущий период и сохранила ее (она составляет (
. Часть занятых в период (t+1) состоит из той части, которая имела работу в предыдущий период и сохранила ее (она составляет (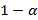 )
) 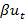 ). Таким образом, вероятность занятости в период (t+1) выражается уравнением
). Таким образом, вероятность занятости в период (t+1) выражается уравнением
 ). Тогда вероятность незанятости в период (t+1) выражается уравнением
). Тогда вероятность незанятости в период (t+1) выражается уравнением

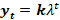 ,
,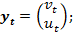
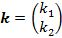 – вектор постоянных величин;
– вектор постоянных величин; 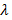 – число, которое находим из необходимого и достаточного условия существования нетривиального решения однородной системы алгебраических уравнений
– число, которое находим из необходимого и достаточного условия существования нетривиального решения однородной системы алгебраических уравнений
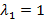 и
и 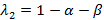 .
.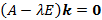
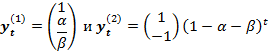
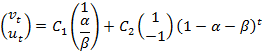
 и
и 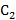 найдем, исходя из того, что при t=0 начальные значения
найдем, исходя из того, что при t=0 начальные значения 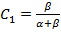 ,
, 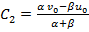
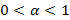 ,
,  ,
, 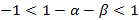 , то
, то 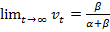 ,
, 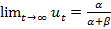 .
.


