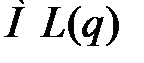Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вероятностный подход к проблеме управления запасамиСодержание книги
Поиск на нашем сайте
Ни одно предприятие не может эффективно функционировать без материально-производственных запасов. Поэтому в условиях современной экономики особую актуальность приобретает проблема управления запасами, ведь само их наличие приносит владельцам лишь убытки и затраты. Под управлением запасами подразумевается оптимизация объема произведенных товаров, незавершенного производства, а также сырья с целью уменьшения суммарных затрат на хранение, доставку и убытков из-за дефицита. Оптимальное управление запасами позволяет предприятию максимально удовлетворять потребности потребителей при эффективной и бесперебойной работе системы с целью максимизации чистой прибыли, и направлено на повышение рентабельности и скорости обращения вложенного капитала. Возникновение теории запасов традиционно связывают с работами Ф. Эджоурта и Ф Харриса в начале ХХ века, посвященных определению экономически выгодного размера партии поставки. Значительное развитие в рамках такой прикладной математической дисциплины, как «исследование операций» данное направление получило в годы второй мировой войны. Одним из наиболее распространенных способов нахождения экономически выгодного размера партии поставки (EOQ-модель) является формула Уилсона, определяющая оптимальный объём заказываемого товара, который позволяет минимизировать общие издержки, связанные с заказом и хранением запасов. В этом случае оптимальный размер партии поставки определяется по формуле:
Для определения оптимального размера партии также применяться различные модификации этой формулы, учитывающие возможность дефицита, непрерывную поставку и другое. Следует отметить, что формула Уилсона изначально разработана для крупных промышленных предприятий. А это означает, что она не может быть применена по своему прямому назначению в современных торговых компаниях. Кроме того, данная формула используется в случае, когда спрос есть величина постоянная. В то же время спрос на сырье и товары часто представляет собой случайный процесс. В случае, когда спрос случайный ставится вопрос нахождения закона распределения случайной величины – размера партии поставки (для дискретной случайной величины) или плотности распределения (если спрос есть непрерывная случайная величина)
Рассмотрим проблему нахождения оптимального размера партии поставки с вероятностным спросом при малых затратах на хранение ( Пусть спрос на некоторый вид продукции в фиксированном интервале времени Определим оптимальный размер партии поставки, минимизирующий суммарные издержки. Поскольку спрос есть случайная величина, найдем математическое ожидание затрат:
Так как
После преобразований двойного неравенства,
Рассчитаем параметры управления запасами по следующим данным. Имеются сведения о распределении вероятностей потребности в определенном виде сырья:
Стоимость единицы сырья составляет 700 грн. В случае его отсутствия на складе убытки оцениваются в 9 000 грн. Определим, какое количество сырья необходимо закупить для минимизации общих затрат на закупку и потери от дефицита. Определим параметр Составим таблицу для вероятностей
Тогда Оптимальный размер партии Найдем математическое ожидание издержек:
Для сравнения составим таблицу значений математического ожидания затрат для всех значений потребностей в сырье:
Как видим, расчетные данные подтверждают полученный результат. Таким образом, при сложившемся процессе производства, при малых затратах на хранение, необходимо заказывать 2 единицы продукции. При этом среднее значение издержек составит 2 430 денежных единиц.
Данную модель можно модифицировать и для случая, когда имеют место затраты на хранение.
Литература:
1. Хруцкий Е.А., Сокович В.А. Колесов С.П. Оптимизация хозяйственных связей и материальных запасов. М.: Экономика, 1977. - 154 с. 2. Гнеденко Б.В., Коваленко И.Н. Введение в теорию массового обслуживания.- М.: «Наука», 1966. 431 с.; черт. — (Физ: — мат. б-ка инженера) 3. Логистика. учеб. пособие/ Б.А. Аникин и др. под редакцией Б.А.Аникина, Т.А. Родниной. – М.: ТК Велби, изд-во Проспект, 2007. – 408 с.
Плотникова Д.В. Полшков Ю.Н. Донецкий национальный университет
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 445; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.109.187 (0.011 с.) |

 , где
, где оптимальный размер партии поставки.
оптимальный размер партии поставки. потребность в товаре за плановый период.
потребность в товаре за плановый период. затраты на хранение, пропорциональны среднему объему запаса на складе.
затраты на хранение, пропорциональны среднему объему запаса на складе. затраты на размещение одного заказа, не зависящее от размера заказа.
затраты на размещение одного заказа, не зависящее от размера заказа.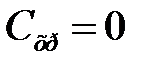 ).
).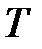 есть случайная величина, имеющая распределение
есть случайная величина, имеющая распределение  . Если в течение рассматриваемого периода спрос
. Если в течение рассматриваемого периода спрос 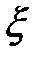 был меньше, чем имеющийся запас
был меньше, чем имеющийся запас  , то его остаток
, то его остаток  , продается с потерями
, продается с потерями  денежных единиц за единицу товара. Если же спрос был больше, чем имеющийся запас, то недостающее количество товара закупается с дополнительными затратами
денежных единиц за единицу товара. Если же спрос был больше, чем имеющийся запас, то недостающее количество товара закупается с дополнительными затратами 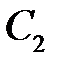 денежных единиц за единицу товара.
денежных единиц за единицу товара.
 – дискретная случайная величина, то минимальное значение находим из системы неравенств:
– дискретная случайная величина, то минимальное значение находим из системы неравенств:
 находим по формуле:
находим по формуле:


 .
.
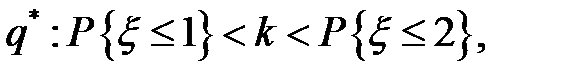 то есть
то есть  .
. .
.