
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вывод закона вынужденных колебаний. Явление резонанса.Содержание книги
Поиск на нашем сайте
Вынужденные колебания Рассмотрим теперь случай, когда в системе наряду с силами упругости и трения присутствует некоторая внешняя сила, препятствующая затуханию колебаний. Предположим, что эта вынуждающая сила Fв действует периодически с круговой частотой wв и зависит от времени по закону: Fв = Fо sin wв t, где Fо - амплитуда вынуждающей силы. Для этого случая дифференциальное уравнение (второй закон Ньютона) имеет вид:
Сохраняя обозначения к / m = w 02 , r / m = 2b, и обозначив F0 /m = f0 приведем уравнение (13) к виду:
Решение этого уравнения представляет некоторую функцию, которая графически представлена на рис. 3. Это решение состоит из двух частей. Одна из них соответствует неустановившемуся режиму колебаний, когда их амплитуда зависит от времени. Вторая часть описывает установившийся режим колебаний. В установившемся режиме вынужденных колебаний смещение х подчиняется гармоническому закону и происходит с частотой, равной частоте действия вынуждающей силы: х = А sin (w в t + jo). (15) Установившаяся амплитуда А вынужденных колебаний, зависит от параметров системы (частоты собственных колебаний w 0 и коэффициента затухания b) и от характеристик вынуждающей силы (f0 и wв): А = f (w0,b, f0,w в). Строгое рассмотрение приводит к следующим выражением для значений А и j0, входящих в формулу (15):
Из рассматриваемой формулы (16) следует, что амплитуда достигает максимального значения Аmах при определенном соотношении между величинами w0,w в и b. Минимум знаменателя в формуле (16) достигается при условии:
То есть, амплитуда вынужденных колебаний максимальна, если частота действия вынуждающей силы определяется формулой (18). Явление резкого возрастания амплитуды вынужденных колебаний при частоте действия вынуждающей силы, определяемой формулой (16), называется резонансом. Если бы затухание в системе отсутствовало (b = 0), то резонанс наступал бы при условии (w0 = w в) и при этом амплитуда достигала бы бесконечно большого значения. Вопрос 28 Автоколебания. Автоколебания, незатухающие колебания, которые могут существовать в какой-либо системе при отсутствии переменного внешнего воздействия, причём амплитуда и период колебаний определяются
свойствами самой системы. Этим Автоколебания отличаются от вынужденных колебаний, амплитуда и период которых определяются характером внешнего воздействия (приставка «авто» и указывает на то, что колебания возникают в самой системе, а не навязываются внешним воздействием). Автоколебания отличаются и от свободных колебаний (например, колебаний свободно подвешенного маятника, колебаний силы тока в электрическом контуре) тем, что, во-первых, свободные колебания постепенно затухают, во-вторых, их амплитуда зависит от первоначального «толчка», создающего эти колебания. Примерами Автоколебания могут служить колебания, совершаемые маятником часов, колебания струны в смычковых или столба воздуха в духовых музыкальных инструментах, электрические колебания в ламповом генераторе (см. Генерирование электрических колебаний). Системы, в которых возникают Автоколебания, называются автоколебательными. Автоколебательные системы во многих случаях можно разделить на 3 основных элемента: 1) колебательную систему (в узком смысле); 2) источник энергии, за счет которого поддерживаются Автоколебания, и 3) устройство, регулирующее поступление энергии из источника в колебательную систему. Эти 3 основных элемента могут быть отчётливо выделены, например, в часах, в которых маятник или баланс служит колебательной системой, пружинный или гиревой завод — источником энергии, и, наконец, анкерный ход — механизмом, регулирующим поступление энергии из источника в систему. В ламповом генераторе колебательной системой служит контур, содержащий ёмкость и индуктивность и обладающий малым активным сопротивлением; выпрямитель (или батарея), питающий напряжением анод лампы, является источником энергии, а электронная лампа с элементом обратной связи — устройством, регулирующим поступление энергии из источника в колебательный контур. В часах, например, Автоколебания осуществляются следующим образом (рис.). При прохождении качающегося балансира 1 через определённое положение (обычно дважды за период) спусковое устройство 2 и 3 подталкивает колесо балансира, сообщая ему энергию, необходимую для того, чтобы компенсировать потерю энергии за полпериода колебаний. Балансир часов совершает Автоколебания с амплитудой, целиком определяемой свойствами часового механизма. Однако для того, чтобы эти Автоколебания возникли, обычно нужно не только завести пружинный завод, но и слегка встряхнуть часы, т. е. сообщить начальный толчок балансиру. Т. о., часы — это в большинстве случаев автоколебательная система без самовозбуждения. В духовых инструментах продувание струи воздуха поддерживает Автоколебания столба воздуха в трубе инструмента, а в струнных смычковых инструментах Автоколебания поддерживаются силой трения, действующей между смычком и струной. Чтобы колебания были незатухающими, поступающая из источника в систему энергия должна компенсировать потери энергии в самой системе. Такая компенсация происходит в целом за период колебаний; но в одни части периода поступающая энергия может превышать потери в системе, в другие, наоборот, потери в системе могут превышать поступление энергии в неё. То значение амплитуды колебаний, при котором происходит компенсация потерь в целом за период, и является стационарным (не изменяющимся со временем) значением амплитуды Автоколебания Такой баланс поступления и потерь энергии оказывается возможным только при определённых значениях амплитуды Автоколебания (в простейших случаях только при одном значении). Обычно при значениях амплитуды колебаний, меньших стационарной, поступление энергии в систему превышает потери в ней, вследствие чего амплитуда колебаний возрастает и достигает стационарного значения. В частности, если в систему поступает энергия больше, чем теряется в ней при сколь угодно малых амплитудах колебаний, то происходит самовозбуждение колебаний. Наоборот, при амплитудах, превышающих стационарное значение, потери энергии в системе обычно превышают поступление энергии из источника, вследствие чего амплитуда колебаний уменьшается и также достигает стационарного значения. Т. о., отклонения амплитуды Автоколебания в ту или другую сторону от стационарного значения затухают, и Автоколебания в этих случаях устойчивы. Однако в некоторых случаях отклонение амплитуды колебаний от стационарного значения и нарушение компенсации потерь энергии в системе приводят к дальнейшему росту отклонений амплитуды от стационарного значения. Это будет иметь место, если при уменьшении амплитуды потери начинают преобладать над поступлением энергии или, наоборот, при увеличении амплитуды поступление энергии начинает преобладать над потерями. В этом случае Автоколебания неустойчивы, и, вследствие наличия во всякой реальной системе неизбежных возмущений и толчков, такие Автоколебания длительное время существовать не могут. Форма Автоколебания может быть различной. Если добротность колебательной системы велика, т. е. потери энергии в колебательной системе относительно малы, то для поддержания Автоколебания в систему за период должно поступать количество энергии, очень малое по сравнению с полной энергией колебательной системы. При этом характер происходящих процессов почти не изменяется по сравнению с тем, как они протекали бы в системе без поступления энергии. В этом случае период и форма Автоколебания будут очень близки к периоду и форме собственных колебаний колебательной системы; если собственные колебания в системе по форме близки к гармоническим, то Автоколебания также близки к гармоническим. В систему с малой добротностью для поддержания Автоколебания должна поступать энергия, уже не малая по сравнению с энергией системы, что может существенно изменить характер происходящих в ней процессов; в частности, форма Автоколебания может значительно отличаться от синусоидальной. Если за период Автоколебания рассеивается вся накопленная в системе энергия (т. е. система уже не колебательная, а апериодическая), то Автоколебания могут очень сильно отличаться по форме от синусоидальных, т. е. превратиться в т. н. релаксационные колебания. Возможность установления баланса энергии только при определённых значениях амплитуды Автоколебания обусловлена наличием в системе т. н. нелинейного элемента, свойства которого зависят от состояния системы (например, сопротивления, которое зависит от приложенного к этому сопротивлению напряжения). Вопрос 28.1 Параметрический резонанс примеры вление параметрического резонанса возникает в колебательных системах, у которых внешнее воздействие сводится к изменению со временем их параметров, например, частоты колебаний. Для математического описания параметрического резонанса мы должны уравнение гармонических колебаний (21.6) заменить на уравнение
в котором учтено, что в результате внешних воздействий частота собственных колебаний меняется во времени: w = w(t). Выясним условия возникновения параметрического резонанса в важном случае, когда функция w2(t) мало отличается от некоторой постоянной величины
где h<<1, W — частота внешних воздействий. Таким образом, уравнение движения (21.70) приобретает вид
В простейшем случае, когда частота внешнего воздействия в 2 раза больше частоты ее собственных колебаний, т.е. W» w0, приближенное решение этого уравнения можно представить в виде
При этом может реализоваться случай, когда k>1. Тогда амплитуда A(t)=A0tk с течением времени возрастает (рис. 21.23). Такое явление называется параметрическим резонансом. Рассмотрим простейший пример механической колебательной системы — маятник, длина которого периодически изменяется. Пусть в момент времени, когда маятник проходит через положение равновесия, длина нити уменьшается на Dl (рис. 21.24, а), а в момент, когда маятник максимально отклонен от положения равновесия, его длина снова восстанавливается до постоянного значения (рис. 21.24, б).
В момент укорачивания нити внешним силам необходимо произвести работу против сил тяжести и центробежной силы, а в момент удлинения нити выполняется противоположная по знаку работа только силами тяжести (работа центробежной силы равна нулю, так как v=0). Суммарная работа внешних сил за один полупериод положительна и идет на увеличение энергии колебаний маятника. В случае малого трения в системе амплитуда колебаний постепенно возрастает, достигая некоторого максимального значения. Аналогично, изменяя с помощью внешних сил параметры колебательного контура (индуктивность или емкость), можно достичь параметрического резонанса в колебательном контуре. Вопрос 29 Волны. Волна – процесс распространения колебаний в среде. Механические колебания могут распространяться в упругих средах: в твердых телах, в жидкостях и в газах. Колебания отдельной частицы среды вызывает колебания соседней частицы (или частиц), которые возбуждают колебания следующих частиц. Так образуется механическая волна. Если взять резиновый шнур, закрепленный с одного конца, а другой его конец заставить колебаться, например, движением руки вверх-вниз, то мы получим волну, бегущую вдоль шнура. При этом каждая частица шнура будет колебаться в плоскости, перпендикулярной направлению распространения волны. Такая волна называется поперечной волной. Если колебания частиц среды происходят в направлении распространения волны, то такая волна называется продольной волной. При распространении волны частицы не двигаются вместе с волной, а совершают колебания около положения равновесия. Механическая волна не переносит массу вещества в среде, но переносит энергию. Продольные упругие волны могут распространяться в твердых телах, в жидкостях и газах, т.е. в средах, где возникают упругие силы при деформациях растяжения и сжатия. Поперечные упругие волны могут распространяться только в твердых телах, в которых возникают силы упругости при деформациях сдвига. Неупругие поперечные волны могут возникать на поверхности жидкостей под действием сил поверхностного натяжения и силы тяжести. Вы помните, что уравнение гармонических колебаний позволяет описывать колебания во многих системах различной природы, т.е. это уравнение является универсальным и очень полезным, дает нам информацию о параметрах колебательного процесса, о значении колеблющейся величины в любой момент времени. Волну или волновой процесс тоже можно описать аналитически. Очень просто эта задача решается, если колебания в волне гармонические. Такая волна называется гармонической волной. На рис.15.1 представлена гармоническая поперечная волна, распространяющаяся со скоростью υ вдоль оси х,т. е. приведена зависимость между смещением ξ частиц среды, участвующих в волновом процессе, и расстоянием х этих частиц (например, частицы В) от источника колебаний О для какого-то фиксированного момента времени t. Геометрическое место точек, до которых доходят колебания к моменту времени t, называется фронтом волны. Если фронт волны является плоскостью (как в нашем примере), то волна называется плоской волной.
Рис.15.1 где ν – частота колебаний или частота волны. Уравнение плоской волны, распространяющейся вдоль положительного направления оси x, имеет вид:
где x (x,t) — смещение точек среды с координатой x в момент времени t; А — амплитуда волны или амплитуда колебаний в волне; w — циклическая (круговая) частота колебаний; k=2p/l - волновое число; φ =
Вопрос 29.1 Образование волн Волны могут генерироваться различными способами. · Генерация локализованным источником колебаний (излучателем, антенной). · Спонтанная генерация волн в объёме при возникновении гидродинамических неустойчивостей. Такую природу могут иметь, например, волны на воде при достаточно большой скорости ветра, дующего над водной гладью. · Переход волн одного типа в волны другого типа. Например, при распространении электромагнитных волн в кристаллическом твёрдом теле могут генерироваться звуковые волны. Вопрос 29.2
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 640; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.140.108 (0.007 с.) |

 (13)
(13) (14)
(14)
 (16)
(16) (17)
(17) (18)
(18)
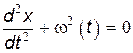 ,
,
 Рис. 21.22
Рис. 21.22
 и является простой периодической функцией (рис. 21.22):
и является простой периодической функцией (рис. 21.22): ,
, .
. Рис. 21.23
Рис. 21.23
 .
.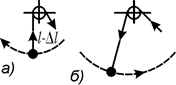 Рис. 21.24
Рис. 21.24
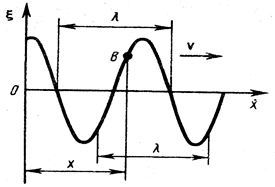 Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длинойволны
Расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, называется длинойволны 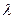 (рис. 15.1). Длина волны
(рис. 15.1). Длина волны 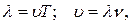 (15.1)
(15.1) , (15.2)
, (15.2) - фаза волны в данной точке среды в данный момент времени. Это уравнение позволяет определить смещение ξ частиц среды с координатой x в любой момент времени t. Из уравнения (15.2) видим, что в данный момент времени t фаза волны для точек с разными координатами x различна. Связь между разностью фаз Dj и разностью хода волны D = x 2 - x 1 определяется формулой:
- фаза волны в данной точке среды в данный момент времени. Это уравнение позволяет определить смещение ξ частиц среды с координатой x в любой момент времени t. Из уравнения (15.2) видим, что в данный момент времени t фаза волны для точек с разными координатами x различна. Связь между разностью фаз Dj и разностью хода волны D = x 2 - x 1 определяется формулой: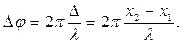 (15.3)
(15.3)


