
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сложение взаимно перпендикулярных колебаний. Фигуры листажуСодержание книги
Поиск на нашем сайте Допустим, что материальная точка может совершать колебания как вдоль оси х, так и вдоль перпендикулярной к ней оси у. Если возбудить оба колебания, материальная точка будет двигаться по некоторой, вообще говоря, криволинейной траектории, форма которой зависит от разности фаз обоих колебаний. Выберем начало отсчета времени так, чтобы начальная фаза первого колебания была равна нулю. Тогда уравнения колебаний запишутся следующим образом:
где — разность фаз обоих колебаний. Выражения (57.1) представляют собой заданное в параметрической форме уравнение траектории, по которой движется тело, участвующее в обоих колебаниях. Чтобы получить уравнение траектории в обычном виде, нужно исключить из уравнений (57.1) параметр t. Из первого уравнения следует, что
Следовательно,
Теперь развернем косинус во втором из уравнений (57.1) по формуле для косинуса суммы, подставляя при этом вместо
Последнее уравнение после несложных преобразований можно привести к виду
Последнее уравнение есть, вообще говоря, уравнение эллипса, оси которого повернуты относительно координатных осей х и у. Ориентация эллипса и величина его полуосей зависят довольно сложным образом от амплитуд а и b и разности фаз
Рис. 57.1,
Рис. 57.2. Определим форму траектории для некоторых частных случаев. 1. Разность фаз а равна нулю. В этом случае уравнение (57.4) принимает вид
откуда получается уравнение прямой
Результирующее движение является гармоническим колебанием вдоль этой прямой с частотой и амплитудой, равной (рис. 57.1). 2. Разность фаз а равна Уравнение (57.4) имеет вид
откуда получается, что результирующее движение представляет собой гармоническое колебание вдоль прямой (рис. 57.2)
3. При уравнение (57.4) переходит в
т. е. в уравнение эллипса, приведенного к координатным осям, причем полуоси эллипса равны соответствующим амплитудам колебаний. При равенстве амплитуд а и эллипс вырождается в окружность. Случаи отличаются направлением движения по эллипсу или по окружности. Если уравнения (57.1) можно записать следующим образом:
В момент тело находится в точке (рис. 57.3). В последующие моменты времени координата х уменьшается, а координата у становится отрицательной. Следовательно, движение совершается по часовой стрелке.
Рис. 57.3.
Рис. 57.4. При уравнения колебаний имеют вид
Отсюда можно заключить, что движение происходит против часовой стрелки. Из сказанного следует, что равномерное движение по окружности радиуса R с угловой скоростью со может быть представлено как сумма двух взаимно перпендикулярных колебаний:
(знак «+» в выражении для у соответствует движению против часовой стрелки, знак «—» — движению по часовой стрелке). В случае, когда частоты взаимно перпендикулярных колебаний отличаются на очень малую величину их можно рассматривать как колебания одинаковой частоты, но с медленно изменяющейся разностью фаз. В самом деле, уравнения колебаний можно представить следующим образом:
и выражение рассматривать как разность фаз, медленно изменяющуюся со временем по линейному закону. Результирующее движение в этом случае происходит по медленно видоизменяющейся кривой, которая будет последовательно принимать форму, отвечающую всем значениям разности фаз от до Если частоты взаимно перпендикулярных колебаний не одинаковы, то траектория результирующего движения имеет вид довольно сложных кривых, называемых фигурами Лиссажу. На рис. 57.4 показана одна из простейших траекторий, получающаяся при отношении частот 1: 2 и разности фаз Уравнения колебаний имеют вид
За то время, пока вдоль оси х точка успевает переместиться из одного крайнего положения в другое, вдоль оси у, выйдя из нулевого положения, она успевает достигнуть одного крайнего положения, затем другого и вернуться в нулевое положение. При отношении частот 1:2 и разности фаз, равной нулю, траектория вырождается в незамкнутую кривую (рис. 57.5), по которой точка движется туда и обратно.
Чем ближе к единице рациональная дробь, выражающая отношение частот колебаний, тем сложнее оказывается фигура Лиссажу. На рис. 57.6 для примера показана кривая для отношения частот 3: 4 и разности фаз Вопрос 24
|
||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 473; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.006 с.) |

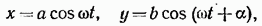


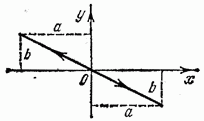
 их значения (57.2) и (57.3). В результате получим
их значения (57.2) и (57.3). В результате получим











 (57.10)
(57.10)






