
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основной закон релятивистской динамики материальной точкиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Масса движущихся релятивистских частиц зависит от их скорости:
где m 0 — масса покоя частицы, т. е. масса, измеренная в той инерциальной системе отсчета, относительно которой частица находится в покое; с — скорость света в вакууме; т — масса частицы в системе отсчета, относительно которой она движется со скоростью v. Следовательно, масса одной и той же частицы различна в разных инерциальных системах отсчета.
Из принципа относительности Эйнштейна, утверждающего инвариантность всех законов природы при переходе от одной инерциальной системы отсчета к другой, следует условие инвариантности уравнений физических законов относительно преобразований Лоренца. Основной закон динамики Ньютона
оказывается также инвариантным по отношению к преобразованиям Лоренца, если в нем справа стоит производная по времени от релятивистского импульса. Основной закон релятивистской динамики материальной точки имеет вид
или
где
— релятивистский импульс материальной точки. Отметим, что уравнение (39.3) внешне совпадает с основным уравнением ньютоновской механики (6.7). Однако физический смысл его другой: справа стоит производная по времени от релятивистского импульса, определяемого формулой (39.4). Таким образом, уравнение (39.2) инвариантно по отношению к преобразованиям Лоренца и, следовательно, удовлетворяет принципу относительности Эйнштейна. Следует учитывать, что ни импульс, ни сила не являются инвариантными величинами. Более того, в общем случае ускорение не совпадает по направлению с силой. В силу однородности пространства в релятивистской механике выполняется закон сохранения релятивистского импульса: релятивистский импульс замкнутой системы сохраняется, т. е. не изменяется с течением времени. Часто вообще не оговаривают, что рассматривают релятивистский импульс, так как если тела движутся со скоростями, близкими к с, то можно использовать только релятивистское выражение для импульса. Анализ формул (39.1), (39.4) и (39.2) показывает, что при скоростях, значительно меньших скорости с, уравнение (39.2) переходит в основной закон (см. (6.5)) классической механики. Следовательно, условием применимости законов классической (ньютоновской) механики является условие v<<c. Законы классической механики получаются как следствие теории относительности для предельного случая v<<c (формально переход осуществляется при с ®¥). Таким образом, классическая механика — это механика макротел, движущихся с малыми скоростями (по сравнению со скоростью света в вакууме). Экспериментальное доказательство зависимости массы от скорости (39.1) является подтверждением справедливости специальной теории относительности. В дальнейшем будет показано, что на основании этой зависимости производятся расчеты ускорителей. Вопрос 41.1 Закон взаимосвязи массы и энергии
Вопрос 41.2
|
||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 794; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.006 с.) |

 (39.1)
(39.1)

 (39.2)
(39.2)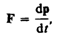 (39.3)
(39.3) (39.4)
(39.4)
 Следовательно,
Следовательно,  .
При υ=c получим, что со скоростью, равной скорости света может двигаться только тело, имеющее массу, равную нулю. Это говорит о предельном характере скорости света для материальных тел.
.
При υ=c получим, что со скоростью, равной скорости света может двигаться только тело, имеющее массу, равную нулю. Это говорит о предельном характере скорости света для материальных тел.
 . Всякое изменение любой энергии (тела, частицы, системы тел) на
. Всякое изменение любой энергии (тела, частицы, системы тел) на  сопровождается пропорциональным изменением массы на Δm.
Нельзя говорить, что при этом масса переходит в энергию. В действительности энергия переходит из одной формы (механической) в другие (электромагнитную и ядерную), но любое превращение энергии сопровождается превращением массы.
сопровождается пропорциональным изменением массы на Δm.
Нельзя говорить, что при этом масса переходит в энергию. В действительности энергия переходит из одной формы (механической) в другие (электромагнитную и ядерную), но любое превращение энергии сопровождается превращением массы.



