Продольные и поперечные волны.

Продольная волна – это волна, при распространении которой смещение частиц среды происходит в направлении распространения волны (рис.1, а).

Причиной возникновения продольной волны является деформация сжатия/растяжения, т.е. сопротивление среды изменению ее объема. В жидкостях или газах такая деформация сопровождается разрежением или уплотнением частиц среды. Продольные волны могут распространяться в любых средах – твердых, жидких и газообразных.

Примерами продольных волн являются волны в упругом стержне или звуковые волны в газах.

Поперечная волна – это волна, при распространении которой смещение частиц среды происходит в направлении, перпендикулярном распространению волны (рис.1,б).

Причиной поперечной волны является деформация сдвига одного слоя среды относительно другого. При распространении поперечной волны в среде образуются гребни и впадины. Жидкости и газы, в отличие от твердых тел, не обладают упругостью по отношению к сдвигу слоев, т.е. не оказывают сопротивления изменению формы. Поэтому поперечные волны могут распространяться только в твердых телах.

Примерами поперечных волн могут служить волны, бегущие по натянутой веревке или по струне.

Волны на поверхности жидкости не являются ни продольными, ни поперечными. Если бросить на поверхность воды поплавок, то можно увидеть, что он движется, покачиваясь на волнах, по круговой траектории. Таким образом, волна на поверхности жидкости имеет как поперечную, так и продольную компоненты. На поверхности жидкости также могут возникать волны особого типа – так называемые поверхностные волны. Они возникают в результате действия силы тяжести и силы поверхностного натяжения.

Рис.1. Продольные (а) и поперечные (б) механические волны

Вопрос 30

Длина волны.

Каждая волна распространяется с какой-то скоростью. Под скоростью волны понимают скорость распространения возмущения. Например, удар по торцу стального стержня вызывает в нем местное сжатие, которое затем распространяется вдоль стержня со скоростью около 5 км/с.

Скорость волны определяется свойствами среды, в которой эта волна распространяется. При переходе волны из одной среды в другую ее скорость изменяется.

Помимо скорости, важной характеристикой волны является длина волны. Длиной волны называется расстояние, на которое распространяется волна за время, равное периоду колебаний в ней.

Поскольку скорость волны — величина постоянная (для данной среды), то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней:

где

v — скорость волны; T — период колебаний в волне; λ (греческая буква «ламбда») — длина волны.

Выбрав направление распространения волны за направление оси x и обозначив через y координату колеблющихся в волне частиц, можно построить график волны. График синусоидальной волны (при фиксированном времени t) изображен на рисунке 45. Расстояние между соседними гребнями (или впадинами) на этом графике совпадает с длиной волны λ.

Формула (22.1) выражает связь длины волны с ее скоростью и периодом. Учитывая, что период колебаний в волне обратно пропорционален частоте, т. е. T = 1/ν, можно получить формулу, выражающую связь длины волны с ее скоростью и частотой:

Полученная формула показывает, что скорость волны равна произведению длины волны на частоту колебаний в ней.

Частота колебаний в волне совпадает с частотой колебаний источника (так как колебания частиц среды являются вынужденными) и не зависит от свойств среды, в которой распространяется волна. При переходе волны из одной среды в другую ее частота не изменяется, меняются лишь скорость и длина волны.

Вопрос 30.1

Уравнение волн

Для получения уравнения волны, то есть аналитического выражения функции двух переменных S = f (t, x), представим что, в некоторой точке пространства возникают гармонические колебания с круговой частотой w и начальной фазой, для упрощения равной нулю (см. рис.8). Смещение в точке М: S_м = A sin w t, где А - амплитуда. Поскольку частицы среды, заполняющие пространство, связаны между собой, то колебания от точки М распространяются вдоль оси х со скоростью v. Через некоторое время D t они достигают точки N. Если в среде отсутсвует затухание, то смещение в этой точке имеет вид: S_N = A sin w (t - D t), т.е. колебания запаздывают на время D t относительно точки M. Поскольку , то заменив произвольный отрезок MN координатой х, получим уравнение волны в виде:

(23)

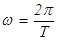Учитывая, что (где Т - период), а длина волны l = v T, формулу (23) можно записать в виде:

(24) Уравнение волны (23) или (24) позволяет определить в любой момент времени t смещение любой точки, имеющей координату х.

Вопрос 31