
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение теплового баланса.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В замкнутой (изолированной от внешних тел) термодинамической системе изменение внутренней энергии какого-либо тела системы ΔU1 не может приводить к изменению внутренней энергии всей системы. Следовательно,
Если внутри системы не совершается работа никакими телами, то, согласно первому закону термодинамики, изменение внутренней энергии любого тела происходит только за счет обмена теплом с другими телами этой системы: ΔUi = Qi. Учитывая
Это уравнение называется уравнением теплового баланса. Здесь Qi - количество теплоты, полученное или отданное i -ым телом. Любое из количеств теплоты Qi может означать теплоту, выделяемую или поглощаемому при плавлении какого-либо тела, сгорании топлива, испарении или конденсации пара, если такие процессы происходят с различными телами системы, и будут определятся соответствующими соотношениями. Уравнение теплового баланса является математическим выражением закона сохранения энергиипри теплообмене. Вопрос 46 Работа при расширении газа
δ A = F·dx = p·S·dx = p·dV (20).
Если F изменяется, то: На рис. б p·dV – это площадь заштрихованной полоски, a При изобарическом процессе (рис. а, кривая I) работа газа:
При изохорическом процессе (рис. а, кривая II) объем не меняется, т. е. dV = 0 и, следовательно, А = 0. При изотермическом процессе меняются и р, и V (рис. б). Заменив давление через объем и температуру, согласно уравнению (4), получим работу газа при T =const:
Проведем процесс расширения газа из состояния 1 (рис. б) в состояние 2 по кривой II (А>0), а сжатие обратно в состояние 1 – по кривой I (А<0). Процесс с возвращением в ту же точку называется циклом. Тогда общая работа будет равна разности площадей под кривыми II и I, т. е. площади цикла. Если цикл на диаграммах p – V совершается по часовой стрелке (см. рис. б), то работа при расширении больше, чем при сжатии и полная работа А > 0. Поскольку мы возвращаемся в ту же точку, ΔU = 0. Из (18) следует, что при таком процессе и теплота, подводимая к телу, должна быть больше нуля (Q > 0). Так происходит в тепловой машине, когда тепло подводится, а машина производит положительную работу. Если же цикл совершается против часовой стрелки, то А < 0. Соответственно и Q < 0, т. е. энергия не подводится к телу, а отводится от него. Это имеет место в холодильнике. В обоих случаях происходит обмен энергией с окружающей средой либо в виде работы, либо в виде обмена теплотой. Вопрос 46.1 Теплоемкость еплоемкость – это количество теплоты, которое необходимо сообщить системе для увеличения ее температуры на 1 Если в качестве системы мы берем индивидуальное вещество, то общая теплоемкость системы
Теплоемкость может быть удельная и молярная. Удельная теплоемкость Молярная теплоемкость Различают истинную и среднюю теплоемкость. В технике обычно используют понятие средней теплоемкости. Средняя Если системе, содержащей количество вещества
Истинная молярная теплоемкость
Согласно уравнению (19), теплоемкость, как и теплота, не является функцией состояния. При постоянном давлении или объеме, согласно уравнениям (11) и (12), теплота, а, следовательно, и теплоемкость приобретают свойства функции состояния, то есть становятся характеристическими функциями системы. Таким образом, получаем изохорную и изобарную теплоемкости. Изохорная теплоемкость
Изобарная теплоемкость
Теплоемкость зависит не только от температуры, но и от объема системы, поскольку между частицами существуют силы взаимодействия, которые изменяются при изменении расстояния между ними, поэтому в уравнениях (20) и (21) используют частные производные. Энтальпия идеального газа, как и его внутренняя энергия, является функцией только температуры:
а в соответствии с уравнением Менделеева–Клапейрона
Поэтому для идеального газа в уравнениях (20), (21) частные производные можно заменить на полные дифференциалы:
Из совместного решения уравнений (23) и (24) с учетом (22), получим уравнение взаимосвязи между
Разделив переменные в уравнениях (23) и (24), можно рассчитать изменение внутренней энергии и энтальпии при нагревании 1 моль идеального газа от температуры
Если в указанном интервале температур теплоемкость можно считать постоянной, то в результате интегрирования получаем:
Установим взаимосвязь между средней и истинной теплоемкостью. Изменение энтропии с одной стороны выражается уравнением (27), с другой –
Приравняв правые части уравнений и выразив среднюю теплоемкость, имеем:
Аналогичное выражение можно получить для средней изохорной теплоемкости. Теплоемкость большинства твердых, жидких и газообразных веществ повышается с ростом температуры. Зависимость теплоемкости твердых, жидких и газообразных веществ от температуры выражается эмпирическим уравнением вида:
где а, b, c и Теплоемкость идеального газа не зависит от температуры. Согласно молекулярно-кинетической теории теплоемкость, приходящаяся на одну степень свободы, равна
Тогда изобарная теплоемкость одноатомного идеального газа согласно (25) определится по уравнению
Двухатомные молекулы идеального газа помимо трех степеней свободы поступательного движения имеют и 2 степени свободы вращательного движения. Следовательно:
Вопрос 47
|
||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 716; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.248.48 (0.009 с.) |


 ,
, На рисунке а приведена зависимость давления газа от его объема. Точка 1 означает состояние газа, так как указывает его давление и объем в данный момент. Температуру при этом можно найти из (4). Линии означают процессы, так как показывают, через какие состояния система проходит. Процесс может быть без изменения давления (прямая I на рисунке а). Такой процесс называется изобарическим. Изохорический процесс (прямая II) – это процесс без изменения объема. Процесс без изменения температуры (изотермический) будет примерно таким, как показано кривой III. Это гипербола, так как при Т = const давление обратно пропорционально объему: p~1/V (см. уравнение (4)). Расширяясь, газ производит работу. Пусть в цилиндре поршень площадью S под действием постоянной силы F передвинулся вследствие расширения газа на расстояние dx. Работа газа будет равна:
На рисунке а приведена зависимость давления газа от его объема. Точка 1 означает состояние газа, так как указывает его давление и объем в данный момент. Температуру при этом можно найти из (4). Линии означают процессы, так как показывают, через какие состояния система проходит. Процесс может быть без изменения давления (прямая I на рисунке а). Такой процесс называется изобарическим. Изохорический процесс (прямая II) – это процесс без изменения объема. Процесс без изменения температуры (изотермический) будет примерно таким, как показано кривой III. Это гипербола, так как при Т = const давление обратно пропорционально объему: p~1/V (см. уравнение (4)). Расширяясь, газ производит работу. Пусть в цилиндре поршень площадью S под действием постоянной силы F передвинулся вследствие расширения газа на расстояние dx. Работа газа будет равна: (21).
(21). – это сумма площадей всех полосок от V 1 до V 2. T. о., работа газа измеряется площадью под кривой на диаграмме p – V. Очевидно, что работа зависит от процесса, т. е. от того, происходит ли расширение газа по кривой I или по кривой II (видно, что на рис. б под кривой II площадь больше, чем под кривой I).
– это сумма площадей всех полосок от V 1 до V 2. T. о., работа газа измеряется площадью под кривой на диаграмме p – V. Очевидно, что работа зависит от процесса, т. е. от того, происходит ли расширение газа по кривой I или по кривой II (видно, что на рис. б под кривой II площадь больше, чем под кривой I). (22).
(22). (23).
(23). (К) при отсутствии полезной работы и постоянстве соответствующих параметров.
(К) при отсутствии полезной работы и постоянстве соответствующих параметров.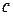 равняется теплоемкости 1 моль вещества (
равняется теплоемкости 1 моль вещества ( ) умноженное на число моль (
) умноженное на число моль ( ).
). . (16)
. (16) – это количество теплоты, необходимое для нагревания единицы массы вещества на 1 град (интенсивная величина).
– это количество теплоты, необходимое для нагревания единицы массы вещества на 1 град (интенсивная величина). – это количество теплоты, необходимое для нагревания одного моль вещества на 1 град.
– это количество теплоты, необходимое для нагревания одного моль вещества на 1 град. – это теплоемкость для определенного интервала температур.
– это теплоемкость для определенного интервала температур. , сообщили количество теплоты
, сообщили количество теплоты  , а температура системы повысилась от
, а температура системы повысилась от 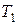 до
до  , то можно рассчитать среднюю удельную или молярную теплоемкость:
, то можно рассчитать среднюю удельную или молярную теплоемкость: ,
,  . (17)
. (17) ,
, 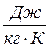 . (18)
. (18) – это отношение бесконечно малого количества теплоты, сообщенной 1 моль вещества при определенной температуре, к приращению температуры, которое при этом наблюдается.
– это отношение бесконечно малого количества теплоты, сообщенной 1 моль вещества при определенной температуре, к приращению температуры, которое при этом наблюдается. . (19)
. (19) – количество теплоты, которое необходимо сообщить системе, чтобы повысить температуру на 1
– количество теплоты, которое необходимо сообщить системе, чтобы повысить температуру на 1  .
. . (20)
. (20) – количество теплоты, которое необходимо сообщить системе, чтобы повысить температуру на 1
– количество теплоты, которое необходимо сообщить системе, чтобы повысить температуру на 1  .
. . (21)
. (21) ,
, , тогда
, тогда . (22)
. (22) . (23)
. (23) . (24)
. (24) . (25)
. (25) . (26)
. (26) . (27)
. (27) . (28)
. (28)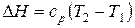 . (29)
. (29) .
. . (30)
. (30) . (31)
. (31) – эмпирические коэффициенты, вычисленные на основе экспериментальных данных о
– эмпирические коэффициенты, вычисленные на основе экспериментальных данных о  , причем коэффициент
, причем коэффициент  – к неорганическим. Значения коэффициентов для различных веществ приведены в справочнике и применимы только для указанного интервала температур.
– к неорганическим. Значения коэффициентов для различных веществ приведены в справочнике и применимы только для указанного интервала температур. (степень свободы – число независимых видов движения на которые можно разложить сложное движение молекулы). Для одноатомной молекулы характерно поступательное движение, которое можно разложить на три составляющие в соответствии с тремя взаимно перпендикулярными направлениями по трем осям. Поэтому изохорная теплоемкость одноатомного идеального газа равна
(степень свободы – число независимых видов движения на которые можно разложить сложное движение молекулы). Для одноатомной молекулы характерно поступательное движение, которое можно разложить на три составляющие в соответствии с тремя взаимно перпендикулярными направлениями по трем осям. Поэтому изохорная теплоемкость одноатомного идеального газа равна . (32)
. (32) . (33)
. (33) ,
,  .
.


