
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференциальные уравнения движения основных звеньевСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
И структурные схемы Уравнение ротора турбогенератора Согласно теореме об изменении момента движения для неустановившегося режима:
где
Если роторы турбины и генератора вращаются с различными скоростями
где
Для установившегося режима ротор вращается равномерно, что возможно в случае равенства момента движущих сил турбины
Вычтем в правых частях почленно уравнение (2) из (1) и введем обозначения:
Тогда уравнение движения ротора примет вид:
Момент действующих сил в турбине может быть выражен таким образом:
где
Если распределительные органы находятся так близко от турбины, что при их перемещении
Момент сил сопротивления генератора для неизменного сопротивления электрической сети можно представить в виде функции:
Уравнения движения ротора составим так, чтобы использовать, что в исследованиях устойчивости регулирования при изучении малых колебаний. Для этого разложим функции
Подставив эти выражения в (3) и обозначив
где
Динамические постоянные Выражение (7) можно привести к виду
где Данное уравнение содержит одну постоянную времени Т, а безразмерный коэффициент Динамические константы вычисляют по заданным характеристикам турбины и генератора. Некоторые характеристики могут быть выражены аналитически, но чаще их задают в виде графиков. В качестве примера на рис. 1 показаны графики изменения вращающегося момента турбины от координаты
Рисунок 1
а) Изменение б) Изменение На рис. 1 представлен график Так как В некоторых системах составляющая
где
Если принять для всех режимов работы турбогенератора (ТГ) одно и тоже среднее значение
Постоянная
Турбина с отбором пара В качестве примера составим уравнение ротора для паровой турбины с одним отбором пара, обладающий двумя группами клапанов (рис.10.3) расположенных перед частью высокого давления (ЧВД) и частью низкого давления (ЧНД) турбины. Положение этих клапанов определим соответственно независимыми координатами Х1 и Х2. Между двумя отсеками турбины расположена камера отбора пара, которая вместе с прилагающими трубами и теплообменными аппаратами составляет объем V, и в этом объеме находится пар под давлением Р. Вращающий момент турбины складывается из моментов М1 и М2, развиваемых соответственно ЧВД и ЧНД турбины. Каждый из этих моментов изменяется в зависимости от положения клапанов перед соответствующим отсеком турбины, от угловой скорости вращения и от давления в камере отбора:
Считаем давления перед турбиной и за него неизменными. Разложив эти функции в степенной ряд и повторив выкладки, сделанные при выводе (7), получим
где
В операторной форме уравнение (12) имеет вид:
где
Рисунок 3 – Схема турбины с отбором пара
Турбина с емкостью В турбинах нередко между распределительными органами и лопаточным аппаратом имеется емкость V (рис. 4).
Рисунок 4 – Схема турбины с емкостью перед лопаточным аппаратом
В таких установках вращающий момент нельзя представить только в зависимости от положения распределительных органов, а надо его выразить в функции от давления
Поступив с этой функцией написанным выражением (10.5), получим уравнение ротора, аналогичное (10.7)
где
Между величинами Х и Турбокомпрессор Если вместо генератора или помимо него, на валу турбомашины находится насос или компрессор, уравнение ротора по существу и по существу и по форме может отличится от уравнения (7). Момент сил сопротивления на валу насоса или компрессора
Эта функция вносит два дополнительных члена в уравнение ротора, которое можно записать, например, для турбины, вращающей компрессор, в таком виде:
где
Для постоянной Если емкости перед компрессором и за ним малы, параметры газа алгебраически связаны со скоростью вращения и три последних члена в левой части (15) можно объединить в один. При этом уравнение ротора принимает вид (7). Уравнение емкости Постоянная емкость Представим себе резервуар неизменной вместимости V, заполненный газом, который принимает в резервуар в единицу времени в количестве На эти расходы газа можно влиять посредством задвижек 1 и 2. При установившемся движении газа
Путем воздействия на распределительные органы нарушим равенство расходов (16). Тогда согласно закону сохранения материи
где
Рисунок 5 Схема аккумулятора газа с постоянным объемом
Разделив обе части (17) на
где Выберем в качестве параметра, характеризующего состояние газа в аккумуляторе, давление
где n – показатель политропы. После дифференцирования (19) найдем:
В уравнение (20) левую и правую часть разделим на
Тогда Рассматривая колебания малыми, считаем что
В (18) введем Тогда
Предположим, что расходы газа G1 и G2 можно представить в виде следующих функций:
где
Подставив (23) и (24) в (22) и представив переменные в относительных единицах, получим уравнение газового объема в форме:
где Динамическая постоянная Динамические постоянные Количество газа, поступающего в резервуар и вытекающего из него, может зависеть от дополнительных параметров по сравнению с принятыми в уравнениях (23) и (24). Так, например, давление перед задвижкой 1 может изменятся В этом случае в уравнении емкости появится дополнительный член с переменной Р1. Допустим, что во всем диапазоне изменений расход G1 линейно зависит от координаты m1. Тогда при n=1 константа Так же как для ротора в предыдущем параграфе, умножим обе части уравнения (25) на R и запишем это уравнение в операторной форме:
где Коэффициенты Переменная емкость Емкость
Правую часть (27) разделим на два слагаемых:
где
Рисунок 6 – Схема аккумулятора газа с переменным объемом
Выполнив разложение функций
где Если массой поршня пренебречь, можно установить алгебраическую связь между его ходом и изменением давления где
Выразив
где
где
Величина Второй член в скобках (30) отражает влияние на процесс регулирования сжимаемости жидкости. ЛЕКЦИЯ №11 Уравнение регулятора
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 658; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.18.135 (0.009 с.) |

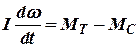 ,
,
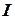 – момент инерции ротора;
– момент инерции ротора;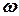 – угловая скорость вращения ротора.
– угловая скорость вращения ротора. ,
,  и их моменты инерции
и их моменты инерции 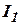 и
и  , то в (1) необходимо подставлять приведенный момент инерции
, то в (1) необходимо подставлять приведенный момент инерции ,
,
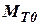 и момента сил сопротивления
и момента сил сопротивления 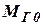
 .
.
 .
.
 .
.
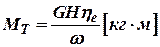 ,
,
 – Расход рабочего тепла турбиной в пч/с;
– Расход рабочего тепла турбиной в пч/с; – удельная теоретическая работа в кг м/кг;
– удельная теоретическая работа в кг м/кг; – эффективный КПД турбины.
– эффективный КПД турбины.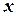 практически мгновенно изменяется расход
практически мгновенно изменяется расход  .
.
 .
.
 и
и 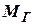 в ряд по степеням
в ряд по степеням 
 и
и 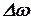 , ограничившись лишь степенями:
, ограничившись лишь степенями: ;
;
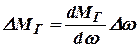 .
.
 ;
;  , получим
, получим ,
,
 ;
;
 .
.
 и
и  имеют размерность времени и являются постоянными турбогенератора.
имеют размерность времени и являются постоянными турбогенератора.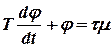 , или в операторной форме
, или в операторной форме ,
,
 .
. не содержит момента инерции ротора и характеризует статические свойства системы.
не содержит момента инерции ротора и характеризует статические свойства системы.
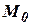 и
и 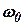 – расчетные величины);
– расчетные величины); .
.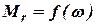 . Графики эти необходимы для вычисления постоянных
. Графики эти необходимы для вычисления постоянных  , а
, а 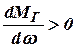 , то
, то  .
. в уравнении (7) играет малую роль, тогда можно записать:
в уравнении (7) играет малую роль, тогда можно записать: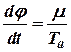 ,
,
 ,
,
 и если предположить, что произошел полный сброс нагрузки и что распределительные органы остаются в открытом положении
и если предположить, что произошел полный сброс нагрузки и что распределительные органы остаются в открытом положении  , то время
, то время  , в течении которого скорость вращения машины достигает ее значения при установившемся движении на холостом ходу, определится из уравнения (10):
, в течении которого скорость вращения машины достигает ее значения при установившемся движении на холостом ходу, определится из уравнения (10): или
или 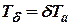
 ,
,  имеет смысл времени разбега ТГ в пределах полного статического изменения скорости вращения
имеет смысл времени разбега ТГ в пределах полного статического изменения скорости вращения 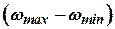 при максимальном и постоянном расходе рабочего тела и неизменных его параметрах.
при максимальном и постоянном расходе рабочего тела и неизменных его параметрах.
 ,
,
 ,
, 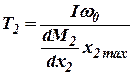 ,
,  ,
, 
 ;
; 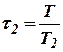 ;
; 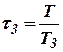 .
.


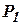 перед турбиной, от которого непосредственно зависит расход и напор:
перед турбиной, от которого непосредственно зависит расход и напор: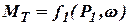 .
.
 ,
,
 ;
;  ;
;  зависит от начальных (
зависит от начальных ( ) параметров рабочего тела и от скорости вращения:
) параметров рабочего тела и от скорости вращения: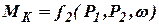 .
. ,
,
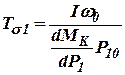 ;
;  ;
;  .
.
 и в то же время вытекает из него в количестве
и в то же время вытекает из него в количестве 
 ,
,
 – удельный вес газа
– удельный вес газа
 и вычитая получено (16) из (17), получим:
и вычитая получено (16) из (17), получим: ,
,
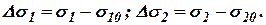
 . Предположим, что во время неустановившегося процесса состояние газа в резервуаре изменяется политропно, то есть:
. Предположим, что во время неустановившегося процесса состояние газа в резервуаре изменяется политропно, то есть: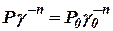 ,
,
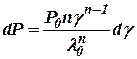 .
.
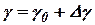 и разложим в ряд (бином Ньютона) выражение:
и разложим в ряд (бином Ньютона) выражение:
 .
. величина малая, а произведение
величина малая, а произведение 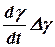 величиной второго порядка малости. Поэтому, отбросив величины второго и высшего порядка малости, последнее уравнение запишем так:
величиной второго порядка малости. Поэтому, отбросив величины второго и высшего порядка малости, последнее уравнение запишем так: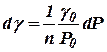 .
.
 вместе
вместе  и обозначим D0 вес газа в данном резервуаре, то есть положим
и обозначим D0 вес газа в данном резервуаре, то есть положим  .
. .
.
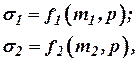
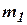 и
и  – координаты, определяющие положения распределительных органов 1 и 2 (рис. 5). При этом давление до задвижки 1 и после задвижки 2 считаем неизменным. Тогда для малых колебаний имеем:
– координаты, определяющие положения распределительных органов 1 и 2 (рис. 5). При этом давление до задвижки 1 и после задвижки 2 считаем неизменным. Тогда для малых колебаний имеем: ,
,
 .
.
 ,
,
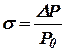 ;
; 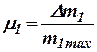 ;
; 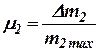 ;
;  ;
; 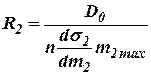 ;
;  .
. имеет положительное значение так как
имеет положительное значение так как 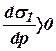 и
и  .
. ,
,  и
и  , а тогда
, а тогда  .
. при полностью открытой задвижки 1 и закрытой задвижки 2, если во время заполнения расход условно считать неизменным и равным расходу для давления
при полностью открытой задвижки 1 и закрытой задвижки 2, если во время заполнения расход условно считать неизменным и равным расходу для давления 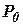 установившегося режима. Аналогичное условное толкование можно дать константе
установившегося режима. Аналогичное условное толкование можно дать константе 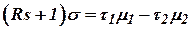 или
или 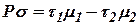
 ;
;  ;
;  .
. и
и  не содержат емкости и носят статический характер.
не содержат емкости и носят статический характер.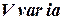 представлена на рис. 6. в виде пространства, к которому подвод и отвод жидкости регулируются распределительными органами 1 и 2 и которые ограничено с одной стороны поршнем 3. Для координат сохраняем обозначения, которыми отмечены соответствующие элементы динамической системы. Уравнение емкости запишем в таком виде:
представлена на рис. 6. в виде пространства, к которому подвод и отвод жидкости регулируются распределительными органами 1 и 2 и которые ограничено с одной стороны поршнем 3. Для координат сохраняем обозначения, которыми отмечены соответствующие элементы динамической системы. Уравнение емкости запишем в таком виде: .
.
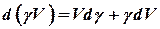 ,
,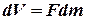 ,
,  – активная площадь поршня.
– активная площадь поршня.
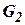 в степенной ряд, вместо (27) получим:
в степенной ряд, вместо (27) получим: ,
,
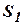 ,
, 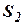 и
и 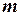 – координаты соответственно распределительных органов и поршня.
– координаты соответственно распределительных органов и поршня. ,
, – жесткость пружины. Согласно последнему уравнению и соотношениям п.2.1, получим
– жесткость пружины. Согласно последнему уравнению и соотношениям п.2.1, получим .
. через
через 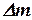 и поделив все члены уравнения (28) на величину
и поделив все члены уравнения (28) на величину 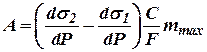 , представим уравнение емкости в виде:
, представим уравнение емкости в виде: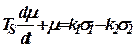 ,
,
 ;
;  ;
;  .
.
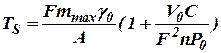 ,
,
 ;
;  .
.
 представляет собой весовое количество жидкости, вытесняемой или всасываемой поршнем в течение его максимального хода. Величина
представляет собой весовое количество жидкости, вытесняемой или всасываемой поршнем в течение его максимального хода. Величина  характеризует изменение расхода жидкости под влиянием изменения давления
характеризует изменение расхода жидкости под влиянием изменения давления 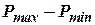 при неизменном положении распределительных органов. Дробь, стоящая перед скобкой
при неизменном положении распределительных органов. Дробь, стоящая перед скобкой  имеет размерность времени.
имеет размерность времени.


