
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Движение тела, брошенного под углом к горизонтуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть тело брошено под углом α к горизонту со скоростью
Рис.29
Начало отсчета совместим с начальным положением тела. Проекции начальной скорости на оси Оу и Ох: Тогда движение тела будет описываться уравнениями:
Из этих формул следует, что в горизонтальном направлении тело движется равномерно, а в вертикальном — равноускоренно. Траекторией движения тела будет парабола. Учитывая, что в верхней точке параболы
Время полета тела находим из условия, что при t=t2 координата у2=0. Следовательно, Время движения тела с максимальной высоты t3=t2-t1=2t1-t1=t1. Следовательно, сколько времени тело поднимается на максимальную высоту, столько времени оно опускается с этой высоты. Подставляя в уравнение координаты х (6) значение времени t2, найдем:
Мгновенная скорость в любой точке траектории направлена по касательной к траектории (см. рис. 29), модуль скорости определяется по формуле
Таким образом, движение тела, брошенного под углом к горизонту или в горизонтальном направлении, можно рассматривать как результат двух независимых движений — горизонтального равномерного и вертикального равноускоренного (свободного падения без начальной скорости или движения тела, брошенного вертикально вверх).
Методические рекомендации по решению задач Рассмотрим, что может быть целью кинематических задач. 1. Нас может интересовать изменение кинематических величин в процессе движения, т.е. получение сведений об изменении координат, скорости, ускорения, а также соответствующих угловых величин. 2. В ряде задач, например, в задаче о движении тела под углом к горизонту, требуется узнать о значениях физических величин в конкретных состояниях: дальности полета, наибольшей величине подъема и т.д. 3. В случаях, когда тело одновременно участвует в нескольких движениях (например, качение шара) или рассматривается относительное движение нескольких тел, возникает необходимость установить соотношения между перемещениями, скоростями и ускорениями (линейными и угловыми), т.е. найти уравнения кинематической связи. Несмотря на большое разнообразие задач по кинематике, можно предложить следующий алгоритм их решения: 1. Сделать схематический рисунок, изобразив начальное положение тел и их начальное состояние, т.е. 2. Выбрать систему отсчета на основании анализа условия задачи. Для этого нужно выбрать тело отсчета и связать с ним систему координат, указав начало отсчета координат, направление осей координат, момент начала отсчета времени. При выборе положительных направлений руководствуются направлением движения (скорости) или направлением ускорения. 3. Составить на основании законов движения систему уравнений в векторном виде для всех тел, а затем в скалярной форме, спроецировав на координатные оси эти векторные уравнения движения. При записи этих уравнений следует обратить внимание на знаки "+" и "-" проекций входящих в них векторных величин. 4. Ответ необходимо получить в виде аналитической формулы (в общем виде), а в конце произвести числовые расчеты.
Пример 4. Сколько времени пассажир, сидящий у окна поезда, который идет со скоростью 54 км/ч, будет видеть проходящий мимо него встречный поезд, скорость которого 36 км/ч, а длина 250 м? Дано: Найти: t.
Решение. Неподвижную систему отсчета свяжем с Землей, подвижную – с поездом, в котором находится пассажир. Согласно закону сложения скоростей
Так как путь, пройденный встречным поездом относительно первого, равен длине поезда, то время
Пример 5. Пароход идет от Нижнего Новгорода до Астрахани 5,0 суток, а обратно - 7,0 суток. Как долго будет плыть плот от Нижнего Новгорода до Астрахани? Стоянки и задержки в движении исключить. Дано: t1=5 сут, t2=7 сут. Найти: t3
Решение. Неподвижную систему отсчета свяжем с берегом, подвижную – с водой. Будем считать, что скорость воды на всем пути одинакова и скорость парохода относительно воды постоянна и равна модулю мгновенной скорости парохода относительно воды. Так как плот движется относительно берега со скоростью течения реки
где Зная время движения, можно найти скорость:
Из формул (1) и (2) имеем:
При движении парохода против течения
С другой стороны,
Решая систему уравнений (3) и (4) относительно
Найдем время движения плота:
t3=35 сут.
Пример 6. При равноускоренном движении тело проходит за два первых равных последовательных промежутка времени по 4,0 с каждый пути s1 = 24 м и s2=64 м соответственно. Определите начальную скорость и ускорение тела. Дано: t1=t2= 4,0 с, s1 =24 м, s2 = 64 м. Найти:
Решение. Запишем уравнения пути для s1 и (s1+s2) соответственно. Так как начальная скорость в этом случае одинакова, то
Так как t1=t2, то
Выразив из (1)
Тогда начальная скорость
Пример 7. Автомобиль, двигаясь по прямолинейной траектории равноускоренно с начальной скоростью 5,0 м/с, прошел за первую секунду путь, равный 6,0 м. Найдите ускорение автомобиля, мгновенную скорость в конце второй секунды и перемещение за 2,0 с. Дано: Найти: Решение. Зная путь, пройденный телом за первую секунду, можно найти ускорение:
Скорость в конце второй секунды найдем по формуле
Перемещение за 2 с можно рассчитать по формулам:
Пример 8. Кинематическое уравнение движения материальной точки по прямой (ось х) имеет вид x = A + Bt + Ct3, где А=4 м, В=2м/с, С=-0,5 м/с3. Для момента времени t1=2 c определить: 1) координату точки х1 точки; 2) мгновенную скорость v1; 3) мгновенное ускорение а1. Дано: x = A + Bt + Ct3, А=4 м, В=2 м/с, С=-0,5 м/с3, t1=2 c. Найти: х1; v1; а1. Решение. 1.Подставим в уравнение движения вместо t заданное значение времени t1: x1 = A + Bt1 + Ct13. Подставим в это выражение значения А, В, С, t1 и произведем вычисления: х1 = 4 м. 2. Мгновенная скорость: 3. Мгновенное ускорение:
Пример 9. Кинематическое уравнение движения материальной точки по прямой (ось х) имеет вид х = A + Bt + Ct2, где А=5 м, В=4м/с, С= -1м/с2. Определить среднюю скорость vхср за интервал времени от t1=1 c до t2=6 c. Дано: х = A + Bt + Ct2, А=5м, В=4м/с, С=- 1м/с2, t1=1 c, t2=6 c. Найти: vхср -? ахср -? Решение. Средняя скорость за интервал времени t2-t1 определяется выражением vср=(х2-х1)/(t2- t1). х1 = A + Bt1 + Ct12= 8 м, х2 = A + Bt2 + Ct22= –7 м. Подставим значения х1, х2, t1, t2 и произведем вычисления: vхср= -3 м/с.
Пример 10. Из вертолета, находящегося на высоте h = 300 м, сбросили груз. Через какое время груз достигнет земли, если: а) вертолет неподвижен; б) вертолет опускается со скоростью v0=5 м/с; 3) вертолет поднимается со скоростью v0=5 м/с. Описать графически соответствующие движения груза в осях s(t), v(t) и a(t).
Решение. а) Груз, покинувший неподвижный вертолет, свободно падает, т.е. движется равноускоренно с ускорением свободного падения g. Время движения найдем из соотношения б) Движение груза, покинувшего вертолет, который опускается с постоянной скоростью v0=5 м/с, является равноускоренным движением с постоянным ускорением g и описывается уравнением
Подстановка численных значений дает уравнение 9,8t2+10t-600=0.
Отрицательный результат не имеет физического смысла, поэтому время движения t=7,57 с. Графики движение объекта отмечены 2 на рисунке. 3) Движение груза, покинувшего вертолет, который поднимается с постоянной скоростью v0=5 м/с, cостоит из двух этапов. На первом этапе – груз движется равнозамедленно с постоянным ускорениемg, направленным противоположно скорости, и описывается уравнениями
В верхней точке траектории скорость становится равной нулю, поэтому
Подставляя второе уравнение системы в первое, получим
На втором этапе – свободное падение с высоты h0=h+h1=300+1,28=301,28 м. Поскольку
Графики движение объекта отмечены 3 на рисунке.
Пример 11. С воздушного шара, опускающегося вниз с постоянной скоростью 2 м/с, бросили вертикально вверх груз со скоростью 18 м/c относительно земли. Определить расстояние между шаром и грузом в момент, когда груз достигает высшей точки своего подъема. Через какое время груз пролетит мимо шара, падая вниз. Дано: v01= 2 м/с, v02=18 м/c Найти: s-? τ -?
Решение. Направим ось 0Y вертикально вверх, начало совместим с точкой 0, в которой находился шар в момент бросания груза. Тогда уравнения движения груза и воздушного шара:
Скорость движения груза изменяется по закону v2=v02 – gt. В наивысшей точке В подъема груза v2=0. Тогда время подъема до этой точки
За это время воздушный шар опустился до точки А; его координата
Расстояние между точками А и В:
Через промежуток времени τ, когда камень пролетит мимо шара, координаты тел будут одинаковы: у1С=у2С;
Отсюда
Пример 12. С какой скоростью и по какому курсу должен лететь самолет, чтобы за два часа пролететь на север 300 км, если во время полета дует северо-западный ветер под углом 30о к меридиану со скоростью 27 км/ч? Дано: t=7,2∙103 c; l =3∙105 м; α=30° ≈ 0,52 рад; v2 ≈7,2 м/с. Найти: v2 -? φ -?
Решение. Рассмотрим движение самолета в системе отсчета, связанной с землей. Проведем ось ОХ в направлении на восток, а ось OY - на север. Тогда скорость движения самолета в выбранной системе отсчета
где v= l /t (2) Уравнение (1) в проекции на оси ОХ: 0=v1∙sinα – v2∙sinφ; OY: v= v2∙cosφ - v1∙cosα, или v1∙sinα = v2∙sinφ, v2∙cosφ=v1∙cosα + v (3) Разделив эти уравнения почленно, получим tgφ=v1sinα/(v1cosα+ v), или с учетом (2) tgφ=v1∙sinα/(v1∙cosα+ l /t); φ=arctgv1∙sinα/(v1∙cosα+ l /t) ≈0,078 рад. Возводя в квадрат правые и левые части уравнений (3) и складывая полученные уравнения, находим v22∙sin2φ + v22 ∙cos2φ = v12 sin2α+ (v1∙cosα + v)2, откуда
Пример 13. Тело, брошенное вертикально вверх, вернулось на землю через t=3 с. Найти высоту подъема тела и его начальную скорость.
Решение. Движение тела вверх является равнозамедленным с ускорением - g и происходит в течение времени t 1, а движение вниз – равноускоренным с ускорением g и происходит в течение времени t 2. Уравнения, описывающие движение на участках АВ и ВА, образуют систему:
Поскольку vB=0, то v0=gt1. Подставив v0 в первое уравнение системы, получим Высота подъема тела
Пример 14. Свободно падающее тело в последнюю секунду движения прошло половину пути. Найти высоту, с которой оно брошено и время движения.
Решение. Зависимость пройденного пути от времени для свободно падающего тела Решая систему
получим t2-4t+2=0. Корни этого уравнения t1=3,41 с и t2=0,59 с. Второй корень не подходит, т.к. время движения, исходя из условия задачи, должно превышать одну секунду. Следовательно, тело падало в течение 3,41 с и прошло за это время путь
Пример 15. С башни высотой 25 м горизонтально брошен камень со скоростью 15 м/с. Найти: 1) сколько времени камень будет в движении, 2) на каком расстояниион упадет на землю, 3) с какой скоростью он упадет на землю, 4) какой угол составит траектория камня с горизонтом в точке его падения на землю. Сопротивление воздуха не учитывать. Дано: Н=25 м, vo=15 м/с Найти: t-? sx-? v -? φ-?
Решение. Перемещение брошенного горизонтально камня можно разложить на два: горизонтальное sx и вертикальное sy: sy=H=gt2/2, sx=vot, где t - время движения. Отсюда:
2) sx=vot= 33,9 м; 3) vy=gt=22,1м/с; 4) sinφ= vy/v=0,827; φ=55о48’. Пример 16. С башни высотой 25 м горизонтально со скоростью vx=10 м/c брошено тело. Найти: 1) время t падения тела, 2) на каком расстоянии l от основания башни оно упадет, 3) скорость v в конце падения, 4) угол, который составит траектория тела с землей в точке его приземления.
Решение. Движение тела является сложным. Оно участвует в равномерном движении по горизонтали и равноускоренном с ускорением g по вертикали. Поэтому участок АВ описывается уравнениями:
Для точки А эти уравнения принимают вид:
Тогда l =10∙2,26=22,6 м, а vy=9,8∙2,26=22,15 м/с. Поскольку Угол, который траектория составляет с землей, равен углу φ в треугольнике скоростей в т. А, тангенс которого Пример 17. Для тела, брошенного с горизонтальной скоростью vx=10 м/с, через время t=2 с после начала движения найти: нормальное, тангенциальное и полное ускорения, а также радиус кривизны траектории в этой точке.
Решение. Вертикальная составляющая скорости vy=gt=9,8∙2=19,6 м/с Скорость в точке А:
Векторы Отсюда,
Нормальное ускорение
Пример 18. Мяч бросили со скоростью 10 м/с под углом 40о к горизонту. Найти: 1) на какую высоту поднимется мяч; 2) на каком расстоянии от места бросания мяч упадет на землю, 3) сколько времени он будет в движении. Дано: vo=10 м/с, α=40о. Найти: sy -? sx -? t -?
Решение. 1) Найдем наибольшую высоту sy max, на которую поднимается тело, брошенное со скоростью vo подуглом α к горизонту. Имеем (см. рис.): vy=vo sinα – gt; (1) sy=vot∙sinα – gt2/2. (2) В верхней точке vy = 0 и из (1) получим vo∙sin𝛼 = gt1, отсюда время подъема мяча t1=vo∙sinα/g. Подставляя t1 в (2), получим sy max= vo2 ∙sin2α/(2g)= 2,1 м. 2) Найдем дальность полета sx max тела, брошенного под углом к горизонту. Имеем: vx=v o ∙cosα, (3) sx=vxt=vot∙cosα. (4) Тело упадет на горизонтальную плоскость через время t2=2t1=2vosinα/g. Подставляя t2 в (4), получим sxmax = vо2sin2α/ g= 10,0 м. 3) t2=2t1=2vosinα/g=1,3 с.
Пример 19. Тело брошено со скоростью v0=10 м/с2 под углом α=30° к горизонту. На какую высоту тело поднимется. На каком расстоянии от места бросания оно упадет на землю? Какое время он будет в движении?
Решение. Горизонтальная и вертикальная составляющие начальной скорости
Движение на участке ОА можно разложить на два простых движения: равномерное по горизонтали и равнозамедленное по вертикали:
В точке А
Тогда Если тело участвует одновременно в нескольких движениях, то в каждом из них оно участвует независимо от другого, следовательно, время движения на участке АВ определяется временем движения вниз – t2. Время движения вверх равно времени движения вниз, а, значит, При равномерном движении по горизонтали за равные промежутки времени тело проходит равные участки пути, следовательно,
Дальность полета
Высота подъема тела
Пример 20. Точка движется прямолинейно на плоскости по закону x=4(t-2)2. Каковы начальная скорость v0 и ускорение точки a? Найти мгновенную скорость точки vt=5 в начале пятой секунды движения. Решение. 1) Т.к. v=x’, то v0=(4∙(t-2)2)’=(4∙(t2-4t+4))’=(4t2-16t+16)’=8t-16 при t=0 v0=-16 м/с. 2) Т.к. a= 3) При t=4, т.к. до начала 5 с прошло 4 с. vt=5=8t-16=8∙4-16=32 м/с. Ответ: Начальная скорость точки v0=-16 м/с, ускорение a=8 м/с, скорость точки в начале пятой секунды движения vt=5=32 м/с.
Пример 21. Движение материальной точки описывается уравнениями: а) s=αt3; б) s=αt2+βt. Сравните среднюю скорость Решение. Вспомним определения средней и мгновенной скорости:
Выражения для мгновенной скорости получаются путем дифференцирования уравнения движения.
Выражения для средней скорости находятся как отношение изменения криволинейной координаты к времени:
Получим выражения для среднеарифметической скорости:
Ответим на вопрос условия задачи. Видно, что в случае “а” средняя и среднеарифметическая скорости не совпадают, а в случае “б” - совпадают.
Пример 22. Материальная точка движется равномерно по криволинейной траектории. В какой точке траектории ускорение максимально?
Решение. При движении по криволинейной траектории ускорение складывается из тангенциального и нормального. Тангенциальное ускорение характеризует быстроту изменения величины (модуля) скорости. Если величина скорости не изменяется, тангенциальное ускорение равно нулю. Нормальное ускорение зависит от радиуса кривизны траектории an= v 2/R. Ускорение максимально в точке с наименьшим радиусом кривизны, т.е. в точке С.
Пример 23. Материальная точка движется согласно закону: 1) Определить начальную координату, начальную скорость и ускорение путем сравнения с законом движения с постоянным ускорением. Записать уравнение для проекции скорости. Решение. Закон движения с постоянным ускорением имеет вид
Сравнивая это уравнение с уравнением условия задачи, получаем x 0 = - 1 м, v 0x = 1 м/с, a x = - 0,25 м/с2. Возникает вопрос: какой смысл имеет знак “минус”? Когда проекция вектора отрицательна? Только в том случае, когда вектор направлен против оси координат. Изобразим на рисунке начальную координату, векторы скорости и ускорения.
Запишем уравнение для скорости в виде
и подставим в него полученные данные (начальные условия)
2) Найти зависимость скорости и ускорения от времени, применяя определения этих величин. Решение. Применим определения для мгновенных значений скорости и ускорения:
Производя дифференцирование, получим v x=1-0,25t, ax = - 0,25 м/с2. Видно, что ускорение не зависит от времени. 3) Построить графики vх(t) и aх(t). Охарактеризовать движение на каждом участке графика. Решение. Зависимость скорости от времени - линейная, график представляет собой прямую линию. При t = 0 vх = 1 м/с. При t = 4 с vх = 0.
Из графика видно, что на участке “а” проекция скорости положительная, а ее величина убывает, т.е. точка движется замедленно в направлении оси х. На участке “b” проекция скорости отрицательная, а ее модуль возрастает. Точка движется ускоренно в направлении, противоположном оси х. Следовательно, в точке пересечения графика с осью абсцисс происходит поворот, изменение направления движения. 4) Определить координату точки поворота и путь до поворота. Решение. Еще раз отметим, что в точке поворота скорость равна нулю. Для этого состояния из уравнений движения получаем:
Из второго уравнения получаем t пов = 4 с. (Видно, чтобы получить это значение не обязательно строить и анализировать график). Подставим это значение в первое уравнение: xпов=-1+4-42/8 = 1 м. Изобразим, как двигалась точка.
Путь до поворота, как видно из рисунка, равен изменению координаты: sпов=xпов-x0=1-(-1)=2 м. 5) В какой момент времени точка проходит через начало координат? Решение. В уравнении движения следует положить х = 0. Получаем квадратное уравнение 0=-1+t-t2/8 или t2-8t+8=0. У этого уравнения два корня: 6) Найти путь, пройденный точкой за 5 секунд после начала движения, и перемещение за это время, а также среднюю путевую скорость на этом участке пути. Решение. Прежде всего найдем координату, в которой оказалась точка после 5 секунд движения и отметим ее на рисунке. x(5)=-1+5-52/8= 0,875 м.
Поскольку в данном состоянии точка находится после поворота, то пройденный путь уже не равняется изменению координаты (перемещению), а складывается из двух слагаемых: пути до поворота s1 = xпов - x0 = 1 - (-1) = 2 м и после поворота s2 = xпов - x(5) = 1 - 0,875 = 0,125 м, s = s1 + s2 = 2,125 м. Перемещение точки равно sх = x(5) - x0 = 0,875 - (-1) = 1,875 м Средняя путевая скорость вычисляется по формуле
В рассмотренной задаче описан один из наиболее простых видов движения - движение с постоянным ускорением. Тем не менее, данный подход к анализу характера движения является универсальным.
Пример 24. При одномерном движении с постоянным ускорением зависимости координаты и скорости частицы от времени описываются соотношениями:
Установить связь между координатой частицы и ее скоростью. Решение. Из этих уравнений исключаем время t. Для этого используем метод подстановки. Из второго уравнения выражаем время
Если движение начинается из начала координат (х 0 =0) из состояния покоя (v 0x =0), то полученная зависимость принимает вид
хорошо знакомый из школьного курса физики.
Пример 25. Движение материальной точки описывается уравнением: Решение. Условие задачи сформулировано с применением векторного способа описания движения. Перейдем к координатному способу. Коэффициенты при единичных векторах представляют собой проекции вектора скорости, а именно:
Вначале получим зависимости x(t) и y(t), решая задачу первого класса.
Из полученных уравнений исключим время t. Из первого уравнения
Обратим внимание, что координата х должна быть отрицательной, что соответствует положительным значениям времени t.
Пример 26. Частица движется в положительном направлении оси x так, что ее скорость меняется по закону Решение. Установим уравнения, связывающие v и x. По условию задачи Отсюда Разделяя переменные
Искомую зависимость скорости от времени можно получить, применяя любое из двух исходных уравнений. Например,
Пример 27. Частица движется в положительном направлении оси x так, что ее ускорение меняется по закону a=α-βx, где α и β - положительные постоянные. Учитывая, что в момент времени t = 0 она покоилась и находилась в начале координат (x 0 = 0), найдем зависимость скорости частицы от координаты. Решение. Установим уравнения, связывающие а и x. a=α-βx, (1)
В эти три уравнения входят четыре переменных: x, v, a, t. Исключим a и t. Выразим из (2)
С учетом выражения (1) получаем дифференциальное уравнение
Разделяя переменные
и производя интегрирование
получаем
Искомая зависимость скорости от координаты имеет вид
Пример 28. С башни высотой h бросили камень со скоростью v 0 под углом α к горизонту. Найти: 1) какое время камень будет в движении; 2) на каком расстоянии s он упадет на землю; 3) с какой скоростью он упадет на землю; 4) какой угол β составит траектория камня с горизонтом в точке его падения; 5) нормальное и тангенциальное ускорения камня в этой точке, а также радиус кривизны траектории; 6) наибольшую высоту подъема камня. Сопротивлением воздуха пренебречь. Решение. На примере этой задачи покажем, как в обобщенном виде можно установить приведенный алгоритм решения любой задачи данного класса. 1. В задаче рассматривается движение материальной точки (камня) в поле силы тяжести Земли. Следовательно, это движение с постоянным ускорением свободного падения g, направленным вертикально вниз. <
|
||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 2210; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.162.166 (0.014 с.) |

 . Как и в предыдущих случаях, будем пренебрегать сопротивлением воздуха. Для описания движения необходимо выбрать две оси координат — Ох и Оу (рис. 29).
. Как и в предыдущих случаях, будем пренебрегать сопротивлением воздуха. Для описания движения необходимо выбрать две оси координат — Ох и Оу (рис. 29).
 ,
,  . Проекции ускорения:
. Проекции ускорения:  ,
, 
 (6)
(6) (7)
(7) (8)
(8)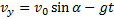 (9)
(9) , можно найти время подъема тела до верхней точки параболы:
, можно найти время подъема тела до верхней точки параболы:


 — максимальная высота подъема тела.
— максимальная высота подъема тела. . Отсюда,
. Отсюда,  — время полета тела. Сравнивая эту формулу с формулой (10), видим, что t2=2t1.
— время полета тела. Сравнивая эту формулу с формулой (10), видим, что t2=2t1.
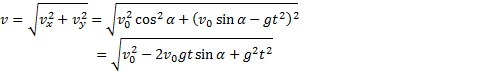
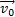 и
и 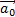 .
.

 , где
, где  - скорость встречного поезда относительно первого. В проекциях на ось Ох:
- скорость встречного поезда относительно первого. В проекциях на ось Ох: .
.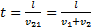 , t=10 c.
, t=10 c.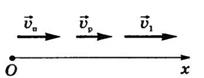
 , то время его движения
, то время его движения  , где s – расстояние между городами. При движении парохода по течению его скорость согласно закону сложения скоростей
, где s – расстояние между городами. При движении парохода по течению его скорость согласно закону сложения скоростей 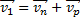 , или в проекциях на ось Ох:
, или в проекциях на ось Ох: (1)
(1) - скорость парохода относительно берега,
- скорость парохода относительно берега,  - скорость парохода относительно реки.
- скорость парохода относительно реки. (2)
(2) (3)
(3) , или в проекциях на ось Ох
, или в проекциях на ось Ох  , где
, где  - скорость парохода относительно берега.
- скорость парохода относительно берега.
 . Тогда
. Тогда (4)
(4) , получим:
, получим:

 .
.

 (2)
(2)


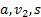



 Тогда в момент времени t1 мгновенная скорость v1 = B + 3Ct12. Подставим сюда значения В,С, t1: v1= – 4 м/с. Знак минус указывает на то, что в момент времени t1=2 c точка движется в отрицательном направлении координатной оси.
Тогда в момент времени t1 мгновенная скорость v1 = B + 3Ct12. Подставим сюда значения В,С, t1: v1= – 4 м/с. Знак минус указывает на то, что в момент времени t1=2 c точка движется в отрицательном направлении координатной оси. Мгновенное ускорение в момент времени t1 равно а1 = 6Сt1. Подставим значения С, t1: а1= –6 м/с2. Знак минус указывает на то, что направление вектора ускорения совпадает с отрицательным направлением координатной оси, причем в условиях данной задачи это имеет место для любого момента времени.
Мгновенное ускорение в момент времени t1 равно а1 = 6Сt1. Подставим значения С, t1: а1= –6 м/с2. Знак минус указывает на то, что направление вектора ускорения совпадает с отрицательным направлением координатной оси, причем в условиях данной задачи это имеет место для любого момента времени.
 Откуда
Откуда  Графики движение объекта отмечены 1 на рисунке.
Графики движение объекта отмечены 1 на рисунке.







 Координата груза в точке В
Координата груза в точке В





 (1)
(1) , или с учетом (2)
, или с учетом (2)


 . Если сравнить это выражение с третьим уравнением системы, то можно сделать вывод о том, что время подъема равно времени спуска t1=t2=t/2=1,5с. Начальная скорость и скорость при приземлении равны друг другу и составляют v0=vA=gt1=9,8∙1,5=14,7 м/с.
. Если сравнить это выражение с третьим уравнением системы, то можно сделать вывод о том, что время подъема равно времени спуска t1=t2=t/2=1,5с. Начальная скорость и скорость при приземлении равны друг другу и составляют v0=vA=gt1=9,8∙1,5=14,7 м/с.
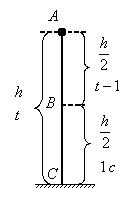
 . Поскольку участок ВС, составляющие половину всего пути, пройден за время, равное 1 с, то первая половина пути АВ пройдена за время (t-1) с. Тогда движение на участке ВС может быть описано как
. Поскольку участок ВС, составляющие половину всего пути, пройден за время, равное 1 с, то первая половина пути АВ пройдена за время (t-1) с. Тогда движение на участке ВС может быть описано как 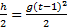 .
.






 , то
, то 
 , поэтому φ=68,7°.
, поэтому φ=68,7°.

 образуют треугольник скоростей, а векторы
образуют треугольник скоростей, а векторы  - треугольник ускорений. Как видно из рисунка, эти треугольники подобны, а это означает, что их стороны пропорциональны:
- треугольник ускорений. Как видно из рисунка, эти треугольники подобны, а это означает, что их стороны пропорциональны:  .
.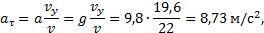
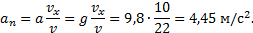
 , поэтому радиус кривизны траектории
, поэтому радиус кривизны траектории


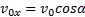


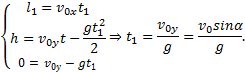
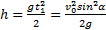 и
и 

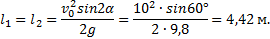


 , то a=(8t-16)’=8 м/с.
, то a=(8t-16)’=8 м/с. и среднеарифметическую начальной и конечной скоростей v ср в интервале времени 0 - t. Здесь α и β - положительные постоянные.
и среднеарифметическую начальной и конечной скоростей v ср в интервале времени 0 - t. Здесь α и β - положительные постоянные.














 . t1 = 1,17 с, t2 = 6,83 с. Действительно, точка проходит через начало координат два раза: при движении “туда” и “обратно”.
. t1 = 1,17 с, t2 = 6,83 с. Действительно, точка проходит через начало координат два раза: при движении “туда” и “обратно”.


 и подставляем в первое уравнение:
и подставляем в первое уравнение:

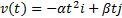 , где i и j - орты осей х и у, α и β - положительные постоянные. В начальный момент времени частица находилась в точке х0 =у0=0. Найти уравнение траектории частицы у(х).
, где i и j - орты осей х и у, α и β - положительные постоянные. В начальный момент времени частица находилась в точке х0 =у0=0. Найти уравнение траектории частицы у(х).




 . Из второго уравнения получаем
. Из второго уравнения получаем
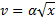 , где α - положительная постоянная. Учитывая, что в момент времени t = 0 она находилась в начале координат (x0 = 0), найти зависимость от времени скорости частицы.
, где α - положительная постоянная. Учитывая, что в момент времени t = 0 она находилась в начале координат (x0 = 0), найти зависимость от времени скорости частицы. .
. (ее исключить проще всего). Получилось дифференциальное уравнение с разделяющимися переменными.
(ее исключить проще всего). Получилось дифференциальное уравнение с разделяющимися переменными. и интегрируя от 0 до t и от 0 до х,
и интегрируя от 0 до t и от 0 до х,  , получаем:
, получаем:  , откуда находим зависимость координаты от времени
, откуда находим зависимость координаты от времени



 и подставим в (3):
и подставим в (3):








