
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Краткие сведения по истории развития кинематикиСодержание книги
Поиск на нашем сайте
Кинематика, как специальный раздел теоретической механики, возникла позднее статики и динамики, а именно, в начале второй половины XIX в. Появление первых исследований по кинематике связано с изобретением огнестрельного оружия. В первую очередь внимание исследователей привлекали вопросы определения траектории полета снаряда, уточнение понятий о неравномерном и криволинейном движении точки. Леонардо да Винчи (1452—1519) первый экспериментально изучал вопрос о свободном вертикальном падении тяжелого тела. Однако лишь благодаря трудам Г. Галилея (1564—1642) развитие механики тесно связывается с запросами техники того времени. Галилею принадлежит введение понятия об ускорении и доказательство того, что траекторией движения снаряда, брошенного в пустоте под некоторым углом к горизонту, является парабола. Законы, найденные Галилеем, были развиты в исследованиях Э. Торричелли (1608—1647), установившем формулу пропорциональности скорости падения тела корню квадратному из высоты падения. Обобщение понятия ускорения на случай криволинейного движения было получено X. Гюйгенсом (1629—1695), который первым обратил внимание на возможность разложения ускорения при криволинейном движении на касательное и нормальное. Однако строгое доказательство этого было дано Л. Эйлером (1707—1783). Кинематические законы движения планет были установлены И. Кеплером (1571—1630). Эти законы легли в основу закона всемирного тяготения, открытого Ньютоном. Л. Эйлеру принадлежат основополагающие исследования по кинематике точки в случае естественного способа задания движения, по кинематике вращательного движения твердого тела вокруг неподвижной точки. Он создал широко применяемый метод кинематического описания движения твердого тела с помощью трех углов, называемых углами Эйлера. Развитие кинематики системы обязано трудам Ж. Лагранжа (1736-1813). Однако только бурный рост машиностроения в XIX в. повлек за собой расцвет кинематики как науки. По предложению Ж. Ампера в 1851 г. кинематика выделилась в особый раздел теоретической механики. Появляется ряд глубоких исследований по кинематике твердого тела французских ученых М. Шаля (1793—1886), Л. Пуансо, Г. Кориолиса (1792—1843). П. Л. Чебышев (1821—1894) создал в России научную школу по кинематике механизмов. Богатое научное наследие по кинематике механизмов Чебышева разрабатывается советскими учеными, среди которых, в первую очередь, следует отметить Н. И.Мерцалова (1860—1948), И. И. Артоболевского, А. П. Котельникова (1865—1940), Д. С. Зернова, Л. В. Асура (1878—1920), Я. Л. Геронимуса и др. «Отцу русской авиации» Н. Е. Жуковскому (1847—1921) принадлежат первоклассные работы по теоретической механике, в том числе и по кинематике, в которых широко внедрены геометрические методы доказательств различных теорем. Ряд замечательных исследований по кинематике принадлежит профессору Одесского университета В. Н. Лигнину (1846—1900), возглавлявшему на Украине научное направление исследований по кинематике.
Кинематика точки. Введение в кинематику. Кинематикой (от греческого «кинема» — движение) называется раздел механики, в котором изучаются геометрические свойства движения тел без учета их инертности (массы) и действующих на них сил. В кинематике изучают зависимости между пространственно-временными характеристиками механического движения. Поэтому кинематику называют также геометрией движения. Основной задачей кинематики является нахождение положения тела в любой момент времени, если известны его положение, скорость и ускорение в начальный момент времени. Обычно кинематику подразделяют на две части — кинематику точки и кинематику твердого тела. Механическое движение - это изменение положения тел (или частей тела) относительно друг друга в пространстве с течением времени. Для определения положения движущегося тела (или точки) в разные моменты времени с телом, по отношению к которому изучается движение, жестко связывают какую-нибудь систему координат, образующую вместе с этим телом систему отсчета. Тело отсчета - тело (или группа тел), принимаемое в данном случае за неподвижное, относительно которого рассматривается движение других тел. Система отсчета - это система координат, связанная с телом отсчета, и выбранный способ измерения времени (рис. 1).
Рис.1
Изображать систему отсчета будем в виде трех координатных осей (не показывая тело, с которым они связаны). Движение тел совершается в пространстве с течением времени. Пространство в механике мы рассматриваем, как трехмерное евклидово пространство. Время является скалярной, непрерывно изменяющейся величиной. В задачах кинематики время t принимают за независимое переменное (аргумент). Все другие переменные величины (расстояния, скорости и т. д.) рассматриваются как изменяющиеся с течением времени, т.е. как функции времени t. В теоретической механике при измерении пространства за основную единицу длины принимают метр (м), а за основную единицу времени — секунду (с). Время предполагается одинаковым в любых системах отсчета (системах координат) и не зависимым от движения этих систем относительно друг друга. Время обозначается буквой и рассматривается как непрерывно изменяющаяся величина, принимаемая в качестве аргумента. При измерении времени в кинематике различают такие понятия, как промежуток времени, момент времени, начальный момент времени. Промежутком времени называется время, протекающее между двумя физическими явлениями. Моментом времени называют границу между двумя смежными промежутками времени. Начальным моментом называется время, с которого начинают отсчет времени. Для решения задач кинематики надо, чтобы изучаемое движение было как-то задано (описано). Кинематически задать движение или закон движения тела (точки) - значит задать положение этого тела (точки) относительно данной системы отсчета в любой момент времени. Основная задача кинематики точки и твердого тела состоит в том, чтобы, зная закон движения точки (тела), установить методы определения всех кинематических величин, характеризующих данное движение. Положение тела можно определить с помощью радиус-вектора Радиус-вектор Координата х точки М - это проекция конца радиуса-вектора точки М на ось Ох. Обычно пользуются прямоугольной системой координат Декарта. В этом случае положение точки М на линии, плоскости и в пространстве определяют соответственно одним (х), двумя (х, у) и тремя (х, у, z) числами - координатами (рис. 2.1).
Рис.2
Рис.2.1
Материальная точка - тело, размерами которого в данных условиях можно пренебречь. Этой моделью пользуются в тех случаях, когда линейные размеры рассматриваемых тел много меньше всех прочих расстояний в данной задаче или когда тело движется поступательно. Основной задачей кинематики точки является изучение законов движения точки. Зависимость между произвольными положениями движущейся точки в пространстве и времени определяет закон ее движения. Закон движения точки считают известным, если можно определить положение точки в пространстве в произвольный момент времени. Положение точки рассматривается по отношению к выбранной системе координат. Поступательным называется движение тела, при котором прямая, проходящая через любые две точки тела, перемещается, оставаясь параллельной самой себе. При поступательном движении все точки тела описывают одинаковые траектории и в любой момент времени имеют одинаковые скорости и ускорения. Поэтому для описания такого движения тела достаточно описать движение его одной произвольной точки. В дальнейшем под словом "тело" будем понимать "материальная точка". Линия, которую описывает движущееся тело в определенной системе отсчета, называется траекторией. На практике форму траектории задают с помощью математических формул (у=f(х) — уравнение траектории) или изображают на рисунке. Вид траектории зависит от выбора системы отсчета. Например, траекторией тела, свободно падающего в вагоне, который движется равномерно и прямолинейно, является прямая вертикальная линия в системе отсчета, связанной с вагоном, и парабола в системе отсчета, связанной с Землей. В зависимости от вида траектории различают прямолинейное и криволинейное движение. Путь s - скалярная физическая величина, определяемая длиной траектории, описанной телом за некоторый промежуток времени. Путь всегда положителен: s> 0. Перемещение
где Проекция перемещения на ось Ох: ∆rx =∆х = х-х0, где x0 и x - координаты тела в начальный и конечный моменты времени. Модуль перемещения не может быть больше пути: Знак равенства относится к случаю прямолинейного движения, если направление движения не изменяется. Зная перемещение и начальное положение тела, можно найти его положение в момент времени t:
Способы задания движения точки Для задания движения точки можно применять один из следующих трех способов: 1) векторный, 2) координатный, 3) естественный. 1. Векторный способ задания движения точки. Пусть точка М движется по отношению к некоторой системе отсчета Oxyz. Положение этой точки в любой момент времени можно определить, задав ее радиус-вектор
Рис.3 При движении точки М вектор
Равенство определяет закон движения точки в векторной форме, так как оно позволяет в любой момент времени построить соответствующий вектор Геометрическое место концов вектора 2. Координатный способ задания движения точки. Положение точки можно непосредственно определять ее декартовыми координатами х, у, z (рис.3), которые при движении точки будут с течением времени изменяться. Чтобы знать закон движения точки, т.е. ее положение в пространстве в любой момент времени, надо знать значения координат точки для каждого момента времени, т.е. знать зависимости x=f1(t), y=f2(t), z=f3(t). Уравнения представляют собой уравнения движения точки в прямоугольных декартовых координатах. Они определяют закон движения точки при координатном способе задания движения. Чтобы получить уравнение траектории надо из уравнений движения исключить параметр t. Нетрудно установить зависимость между векторным и координатным способами задания движения. Разложим вектор
где rx, ry, rz - проекции вектора на оси; Так как начало
Если движение точки задано в полярных координатах r=r(t), φ = φ(t), где r — полярный радиус, φ — угол между полярной осью и полярным радиусом, то данные уравнения выражают уравнение траектории точки. Исключив параметр t, получим r = r(φ). Пример 1. Движение точки задано уравнениями
Рис.4
Чтобы исключить время, параметр t, найдём из первого уравнения sin2t=x/2, из второго cos2t=y/3. Затем возведём в квадрат и сложим. Так как sin22t+cos22t=1, получим Начальное положение точки M 0 (при t =0) определяется координатами x0=0, y0=3 см. Через 1 сек. точка будет в положении M 1 с координатами x1=2sin2=2∙0,91=1,82 см, y1=2cos2=3∙(-0,42)= -1,25 см. Примечание. Движение точки может быть задано с помощью и других координат. Например, цилиндрических или сферических. Среди них будут не только линейные размеры, но и углы. При необходимости, с заданием движения цилиндрическими и сферическими координатами можно познакомиться по учебникам. 3. Естественный способ задания движения точки.
Рис.5
Естественным способом задания движения удобно пользоваться в тех случаях, когда траектория движущейся точки известна заранее. Пусть кривая АВ является траекторией точки М при ее движении относительно системы отсчета Oxyz (рис.5) Выберем на этой траектории какую-нибудь неподвижную точку О', которую примем за начало отсчета, и установим на траектории положительное и отрицательное направления отсчета (как на координатной оси). Тогда положение точки М на траектории будет однозначно определяться криволинейной координатой s, которая равна расстоянию от точки О’ до точки М, измеренному вдоль дуги траектории и взятому с соответствующим знаком. При движении точка М перемещается в положения M 1, М 2,.... следовательно, расстояние s будет с течением времени изменяться. Чтобы знать положение точки М на траектории в любой момент времени, надо знать зависимость s=f(t). Уравнение выражает закон движения точки М вдоль траектории. Функция s= f(t) должна быть однозначной, непрерывной и дифференцируемой. За положительное направление отсчета дуговой координаты s принимают направление движения точки в момент, когда она занимает положение О. Cледует помнить, что уравнение s=f(t) не определяет закон движения точки в пространстве, так как для определения положения точки в пространстве нужно знать еще траекторию точки с начальным положением точки на ней и фиксированное положительное направление. Таким образом, движение точки считается заданным естественным способом, если известна траектория и уравнение (или закон) движения точки по траектории. Важно заметить, что дуговая координата точки s отлична от пройденного точкой по траектории пути σ. При своем движении точка проходит некоторый путь σ, которой является функцией времени t. Однако пройденный путь σ совпадает с расстоянием s лишь тогда,когда функцияs = f(t) монотонно изменяется со временем, т.е. при движении точки в одном направлении. Допустим, что точка М переходит из М1 в М2. Положению точки в М1 соответствует время t1, а положению точки в М2 - время t2. Разложим промежуток времени t2- t1 на весьма малые промежутки времени ∆t1 (i = 1,2, …n) так, чтобы в каждый из них точка совершала движение в одном направлении. Соответствующее приращение дуговой координаты обозначим ∆si. Пройденной точкой путь σ будет положительной величиной:
Если движение точки задано координатным способом, то пройденный путь определяется по формуле
так как
где dx=xdt, dy= ydt, dz=zdt. Следовательно,
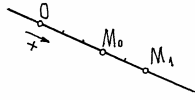
Пример 2. Точка движется по прямой линии, по закону s=2t+3 (см) (рис. 6).
Рис.6
В начале движения, при t=0 s=OM0=s0=3 см. Положение точки M 0 называется начальным положением. При t=1 с, s=OM1=5 см. Конечно, за 1 сек. точка прошла расстояние M 0 M 1 = 2см.Так что s – это не путь пройденный точкой, а расстояние от начала отсчёта до точки.
Вектор скорости точки Одной из основных кинематических характеристик движения точки является векторная величина, называемая скоростью точки. Понятие скорости точки в равномерном прямолинейном движении относится к числу элементарных понятий. Скорость - мера механического состояния тела. Она характеризует быстроту изменения положения тела относительно данной системы отсчета и является векторной физической величиной. Единица измерения скорости – м/с. Часто используют и другие единицы, например, км/ч: 1 км/час=1/3,6 м/с. Движение точки называется равномерным, если приращения радиуса-вектора точки за одинаковые промежутки времени равны между собой. Если при этом траекторией точки является прямая, то движение точки называется прямолинейным. Для равномерно-прямолинейного движения ∆r= v ∆t, (1) где v – постоянный вектор. Вектор v называется скоростью прямолинейного и равномерного движения полностью его определяет. Из соотношения (1) видно, что скорость прямолинейного и равномерного движения является физической величиной, определяющей перемещение точки за единицу времени. Из (1) имеем
Направление вектора v указано на рис. 6.1.
Рис.6.1
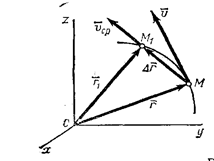
При неравномерном движении эта формула не годится. Введем сначала понятие о средней скорости точки за какой-нибудь промежуток времени. Пусть движущаяся точка находится в момент времени t в положении М, определяемом радиусом-вектором
Рис. 7
Отношение вектора перемещения точки к соответствующему промежутку времени дает векторную величину, называемую средней по модулю и направлению скоростью точки за промежуток времени∆t:
Скоростью точки в данный момент времени t называется векторная величина v, к которой стремится средняя скорость vср при стремлении промежутка времени ∆t к нулю:
Итак, вектор скорости точки в данный момент времени равен первой производной от радиуса-вектора точки по времени. Так как предельным направлением секущей ММ 1 является касательная, то вектор скорости точки в данный момент времени направлен по касательной к траектории точки в сторону движения.
Определение скорости точки при координатном способе задания движения Вектор скорости точки
Таким образом, проекции скорости точки на координатные оси равны первым производным от соответствующих координат точки по времени. Зная проекции скорости, найдем ее модуль и направление (т.е. углы α, β, γ, которые вектор v образует с координатными осями) по формулам
Итак, численная величина скорости точки в данный момент времени равна первой производной от расстояния (криволинейной координаты) s точки по времени. Направлен вектор скорости по касательной к траектории, которая нам наперед известна.
Определение скорости точки при естественном способе задания движения Величину скорости можно определить как предел (∆r – длина хорды ММ 1):
где ∆s – длина дуги ММ 1. Первый предел равен единице, второй предел – производная ds/dt. Следовательно, скорость точки есть первая производная по времени от закона движения:
Направлен вектор скорости, как было установлено ранее, по касательной к траектории. Если величина скорости в данный момент будет больше нуля, то вектор скорости направляется в положительном направлении
Вектор ускорения точки Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости. Оно показывает, на какую величину изменяется скорость тела за единицу времени. В СИ единицей ускорения является метр на секунду в квадрате Пусть в некоторый момент времени t движущаяся точка находится в положении М и имеет скорость v, а в момент t1 приходит в положение M1 и имеет скорость v1 (рис. 8).
Рис.8
Тогда за промежуток времени ∆t=t1-t скорость точки получает приращение Отношение приращения вектора скорости
Вектор среднего ускорения имеет то же направление, что и вектор Ускорением точки в данный момент времени t называется векторная величина Ускорение точки равно нулю лишь тогда, когда скорость точки v постоянна как по величине, так и по направлению: это соответствует только прямолинейному и равномерному движению. Найдем, как располагается вектор При прямолинейном движении с возрастающей по модулю скоростью (рис. 9, а) векторы При прямолинейном движении с убывающей по модулю скоростью (рис. 9, б) направления векторов
Рис.9
Если траекторией точки является плоская кривая, то вектор ускорения
Определение ускорения при координатном способе задания движения Вектор ускорения точки
Или
т.е. проекция ускорения точки на координатные оси равны первым производным от проекций скорости или вторым производным от соответствующих координат точки по времени. Модуль и направление ускорения найдутся из формул
где α1, β1, γ1 - углы, образуемые вектором ускорения с координатными осями. Пример 3. Движение точки задано уравнениями x=2t, y=3-4t2. Из первого уравнения t=x/2. Подставив во второе, получим уравнение траектории: y=3-x2 Это уравнение параболы. В начале движения, при t=0, точка находилась на самом верху, в положении M 0 (x0=0, y0=3 см). А, например, при t =0,5 c она будет в положении M с координатами x1=1 см; y1=2 см. Проекции скорости на оси vx= При t =0,5 c, vx=2см∙с-1, vy=-4 см∙с-1. И модуль скорости Составляющие скорости по осям и вектор её показаны в масштабе на рис. 10.
Рис.10
Проекции ускорения ax=
|
||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 1657; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.189.182.15 (0.01 с.) |


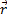 или с помощью координат.
или с помощью координат.

 тела за определенный промежуток времени - направленный отрезок прямой, соединяющий начальное (точка М0) и конечное (точка М) положение тела (см. рис. 2):
тела за определенный промежуток времени - направленный отрезок прямой, соединяющий начальное (точка М0) и конечное (точка М) положение тела (см. рис. 2): ,
, — радиус-векторы тела в эти моменты времени.
— радиус-векторы тела в эти моменты времени. ≤s.
≤s.




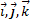 – единичные векторы направленные по осям, орты осей.
– единичные векторы направленные по осям, орты осей.
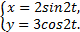
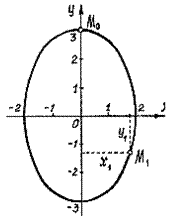
 . Это уравнение эллипса с полуосями 2 см и 3 см (рис.4).
. Это уравнение эллипса с полуосями 2 см и 3 см (рис.4).


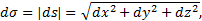



 (рис.7). Тогда перемещение точки за промежуток времени ∆t=t1-t определяется вектором
(рис.7). Тогда перемещение точки за промежуток времени ∆t=t1-t определяется вектором  который будем называть вектором перемещения точки. Из треугольника ОММ 1 видно, что
который будем называть вектором перемещения точки. Из треугольника ОММ 1 видно, что  ; следовательно,
; следовательно, 


 , учитывая, что rx=x, ry=y, rz=z, найдем:
, учитывая, что rx=x, ry=y, rz=z, найдем:


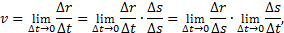

 .
.
 . Для построения вектора
. Для построения вектора 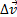 отложим от точки М вектор, равный v 1, и построим параллелограмм, в котором диагональю будет
отложим от точки М вектор, равный v 1, и построим параллелограмм, в котором диагональю будет 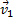 , a одной из сторон
, a одной из сторон  . Тогда, очевидно, вторая сторона и будет изображать вектор
. Тогда, очевидно, вторая сторона и будет изображать вектор 
 , к которой стремится среднее ускорение
, к которой стремится среднее ускорение  при стремлении промежутка времени ∆t к нулю: Вектор ускорения точки в данный момент времени равен первой производной от вектора скорости или второй производной от радиуса-вектора точки по времени.
при стремлении промежутка времени ∆t к нулю: Вектор ускорения точки в данный момент времени равен первой производной от вектора скорости или второй производной от радиуса-вектора точки по времени.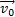 сонаправлены (
сонаправлены ( ) и проекция ускорения на направление движения положительна.
) и проекция ускорения на направление движения положительна. ) и проекция ускорения на направление движения отрицательна.
) и проекция ускорения на направление движения отрицательна.
 в проекции на оси получаем:
в проекции на оси получаем:



 =2см∙с-1, vy=
=2см∙с-1, vy=  =-8t см∙с-1.
=-8t см∙с-1.
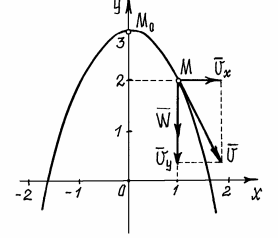
 =0, ay=
=0, ay=  =-8 см∙с-2. Так как проекция вектора ускорения на ось x равна нулю, а на ось y – отрицательна, то вектор ускорения направлен вертикально вниз, и величина его постоянна, не зависит от времени.
=-8 см∙с-2. Так как проекция вектора ускорения на ось x равна нулю, а на ось y – отрицательна, то вектор ускорения направлен вертикально вниз, и величина его постоянна, не зависит от времени.


