
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свободное падение тел. Ускорение свободного паденияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Свободное падение - это движение тела под действием только силы тяжести. На тело, падающее в воздухе, кроме силы тяжести действует сила сопротивления воздуха, следовательно, такое движение не является свободным падением. Свободное падение — это падение тел в вакууме. Ускорение Ускорение свободного падения Галилео Галилей установил (закон Галилея): все тела падают на поверхность Земли под действием земного притяжения при отсутствии сил сопротивления с одинаковым ускорением, т.е. ускорение свободного падения не зависит от массы тела. Убедиться в этом можно, используя трубку Ньютона или стробоскопический метод. Трубка Ньютона представляет собой стеклянную трубку длиной около 1 м, один конец которой запаян, а другой снабжен краном (рис. 25).
Рис.25
Поместим в трубку три разных предмета, например дробинку, пробку и птичье перо. Затем быстро перевернем трубку. Все три тела упадут на дно трубки, но в разное время: сначала дробинка, затем пробка и, наконец, перо. Но так падают тела в том случае, когда в трубке есть воздух (рис. 25, а). Стоит только воздух откачать насосом и снова перевернуть трубку, мы увидим, что все три тела упадут одновременно (рис. 25, б). В земных условиях g зависит от географической широты местности. Наибольшее значение оно имеет на полюсе g=9,81 м/с2, наименьшее — на экваторе g=9,75 м/с2. Причины этого: 1) суточное вращение Земли вокруг своей оси; 2) отклонение формы Земли от сферической; 3) неоднородное распределение плотности земных пород. Ускорение свободного падения зависит от высоты h тела над поверхностью планеты. Его, если пренебречь вращением планеты, можно рассчитать по формуле:
где G — гравитационная постоянная, М — масса планеты, R — радиус планеты. Как следует из последней формулы, с увеличением высоты подъема тела над поверхностью планеты ускорение свободного падения уменьшается. Если пренебречь вращением планеты, то на поверхности планеты радиусом R
Для небольших высот (g<<h) можно считать g=const, для таких высот свободное падение является равноускоренным движением. Для его описания можно использовать формулы равноускоренного движения: уравнение скорости: кинематическое уравнение, описывающее свободное падение тел: или в проекции на ось
Движение тела, брошенного вертикально Свободно падающее тело может двигаться прямолинейно или по криволинейной траектории. Это зависит от начальных условий. Рассмотрим это подробнее.
Свободное падение без начальной скорости ( При выбранной системе координат движение тела описывается уравнениями: Из последней формулы можно найти время падения тела с высоты h:
Подставляя найденное время в формулу для скорости, получим модуль скорости тела в момент падения:
Движение тела, брошенного вертикально вверх с начальной скоростью
Рис.26 Рис.27 Движение тела описывается уравнениями: Из уравнения скорости видно, что тело движется равнозамедленно вверх, достигает максимальной высоты, а затем движется равноускоренно вниз. Учитывая, что при y=hmax скорость
Движение тела, брошенного горизонтально Если скорость Рассмотрим движение тела, брошенного горизонтально с высоты h со скоростью
Рис.28 Тогда движение тела опишется уравнениями:
Анализ этих формул показывает, что в горизонтальном направлении скорость тела остается неизменной, т.е. тело движется равномерно. В вертикальном направлении тело движется равноускоренно с ускорением g, т.е. так же, как тело, свободно падающее без начальной скорости. Найдем уравнение траектории. Для этого из уравнения (3) найдем время
Это уравнение параболы. Следовательно, тело, брошенное горизонтально, движется по параболе. Скорость тела в любой момент времени направлена по касательной к параболе (см. рис. 28). Модуль скорости можно рассчитать по теореме Пифагора:
Зная высоту h, с которой брошено тело, можно найти время t1, через которое тело упадет на землю. В этот момент координата у равна высоте у1=h. Из уравнения (4) находим: Отсюда
|
||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 4522; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.01 с.) |

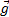 , которое сообщает телу сила тяжести, называют ускорением свободного падения. Оно показывает, на какую величину изменяется скорость свободно падающего тела за единицу времени.
, которое сообщает телу сила тяжести, называют ускорением свободного падения. Оно показывает, на какую величину изменяется скорость свободно падающего тела за единицу времени.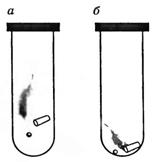
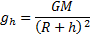

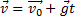
 ,
,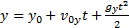 .
.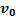 =0) (рис. 26).
=0) (рис. 26).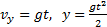 .
.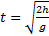 .
.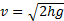 .
.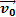 (рис. 27)
(рис. 27)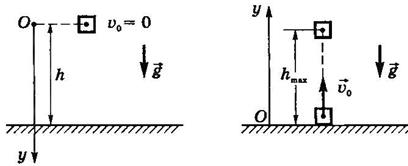
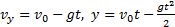
 и в момент достижения телом первоначального положения у=0, можно найти:
и в момент достижения телом первоначального положения у=0, можно найти: — время подъема тела на максимальную высоту;
— время подъема тела на максимальную высоту; — максимальная высота подъема тела;
— максимальная высота подъема тела;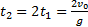 — время полета тела;
— время полета тела;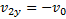 — проекция скорости в момент достижения телом первоначального положения.
— проекция скорости в момент достижения телом первоначального положения.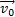 направлена не вертикально, то движение тела будет криволинейным.
направлена не вертикально, то движение тела будет криволинейным. (рис. 28). Сопротивлением воздуха будем пренебрегать. Для описания движения необходимо выбрать две оси координат — Ох и Оу. Начало отсчета координат совместим с начальным положением тела. Из рис.28 видно, что
(рис. 28). Сопротивлением воздуха будем пренебрегать. Для описания движения необходимо выбрать две оси координат — Ох и Оу. Начало отсчета координат совместим с начальным положением тела. Из рис.28 видно, что 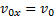 ,
, 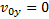 ,
,  ,
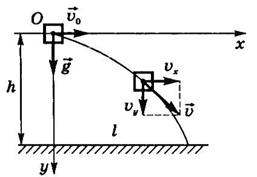
, 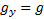 .
.
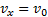 ,
, 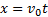 (3)
(3) ,
,  (4)
(4)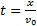 и, подставив его значение в формулу (4), получим:
и, подставив его значение в формулу (4), получим: 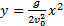
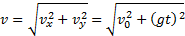
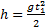

 — дальность полета тела. Модуль скорости тела в этот момент
— дальность полета тела. Модуль скорости тела в этот момент  .
.


