
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изучение физического маятника и определение ускорения силы тяготенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Физическим маятником называют тело, способное осуществлять колебание вокруг недвижимой точки, которая не совпадает с его центром массы (рис.1). Отсюда вытекает, что в положении равновесия физического маятника его центр масс С находится на вертикали с точкой подвеса О, но ниже от нее. При отклонении маятника от положения равновесия на угол
где I – момент инерции тела относительно горизонтальной оси, которая проходит через точку О (ось перпендикулярная к площади рисунка), m – масса маятника; знак минус указывает на то, что момент силы тяготения старается возвратить маятник к положению равновесия, а угол отклонения
или
Величина
Величина
Величину Точку
где
где
Из рис.1 видно, что
Из равенств приведенных длин вытекает равенство периодов колебаний относительно осей, которые проходят через сопряженные точки
В физическом маятнике можно сделать передвижни опорные призмы, или изменять положение отдельных его частей. Если центр качания будет при этом расположенный в пределах тела, то можно достичь такого положения, что маятник будет оборотным, т.е. выбранные его две точки опоры станут сопряженными. Оборотные маятники изготовляют разных конструкций. В данной задаче применяют оборотный маятник, который изображен на рис.2. Он состоит из однородного стержня, на котором есть шкала и передвижные опорные призмы П и грузы Г1 и Г2, которые могут закрепляться в любом месте стержня. Перед началом измерений необходимо выбрать такие условия опыта, чтобы точность измерений была наибольшей. Проведены такие оценки. Для этого перепишем (4) в виде
Графическая зависимость периода колебаний Т от расстояния а изображена на рис.3. С цьогo графика видно, что при приближении точки подвеса к центру масс С (а1
и, если пренебречь
Если разложить это выражение в ряд по степеням
Если периоды Т1 и Т2 полностью совпадают, то (8) переходит в (6). Учитывая (8) и (6), получим для относительной погрешности, обусловленной тем, что периоды Т1 и Т2 не совпадают:
Из (9) видим, что погрешность неограниченно возрастает, если
Предыдущие исследования позволяют всегда расположить призмы и грузы так, чтобы выполнялось это условие. Для этого у маятника, который применяется в нашей лаборатории, следует разместить: 1) призмы П на 5-м и 85-м делениях; 2) грузГ2 в интервале от 30-го и до 60-го деления шкалы; 3) груз Г1на 91-м делению. Чтобы найти приведенную длину маятника, будем изменять его момент инерции I относительно точки подвеса до тех пор пока точки, в которых закрепленны призмы П, станут сопряженными. Это состояние можно достичь определенным расположением груза. Для этого грузГ1 следует передвигать в интервале от 91-го до 115-го деления стержня и через каждые 3 см определять период колебаний маятника. Эти определения надо повторять трижды при это необходимо наблюдать 25 полных колебаний. Полученные средние значения периодов нанесите на график в зависимости от положения груза Г1 . На оси абцис отложите деления шкалы стержня маятника, а на оси ординат – величины периодов колебаний. После этого переверните маятник и придавайте ему колебания на второй опорной призме П. Снова передвигайте груз Г1на 3см в интервале от 115-го до 91-го деления и каждый раз определяйте период колебаний маятника. Эти значения периодов нанесите на график. Точка сечения кривых определит положение груза Г1 , при котором периоды колебаний маятника Т1 и Т2 в прямом и перевернутом положениях наиболее близки друг к другу. ГрузГ1закрепите в положении, которое отвечает точке сечения кривых и определите время 100 полных колебаний не меньше трех раз в прямом положении маятника и так же определите период 100 колебаний повторенных три раза для перевернутого маятника. Если периоды Т1 и Т2 для прямого и обратного маятника не отличаются больше чем на 0,003, то для вычисления ускорения свободного падения g пользуются формулой (6). При расхождении Т1 и Т2на большую величину для расчета g пользуются формулой (8), или формулой Бесселя:
Чтобы определить величины а1 и а2, надо маятник снять с консоли, осторожно положить его на подставку с острой гранью и уравновесить. Расстояние от точки маятника, который находится на грани, до опорных призм дают величины а1 и а2.Измерения а1 и а2выполняют с помощью масштабной линейки с точностью до одного миллиметра. По результатам измерений вычисляют ускорение силы тяготения и оценивают точность эксперимента.
Контрольные вопросы 1. Какое движение носит название колебательного? 2. Определить состояние механического равновесия. Какими являются условия пребывания механической системы в состоянии равновесия? Какое равновесие является устойчивым, а какое - неустойчивым? При каких условиях в механической системе может возникнуть колебательное движение? 3. Какие колебания назваются свободными, или собственными? От чего зависит частота собственных колебаний? 4. Какие колебания называют гармоничными? Что такое фаза гармоничных колебаний и что она характеризует? Как связанны между собой фазы, координаты, скорости и ускорение тела, которое осуществляет гармоничные колебания? От чего зависят амплитуда, частота и начальная фаза гармоничных колебаний? 5. Какую систему называют математическим маятником? Какими параметрами определяется период колебаний математического маятника. Опишите колебание математического маятника. Постройте схематические графики зависимости ускорения, скорости и координаты от времени. 6. Дайте определение физического маятника. Что называется приведенной длиной физического маятника и его центром колебаний. Какие точки маятника являются сопряженными? 7. Какие есть методы нахождения приведенной длины физического маятника? Какая связь существует между ускорением свободного падения и приведенной длиной и периодом колебаний физического маятника. Почему ускорение свободного падения в разных широтах разное? РАБОТА №13
|
||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1355; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.007 с.) |

 возникает вращательный момент М силы тяготения, плечо которой
возникает вращательный момент М силы тяготения, плечо которой  . Он старается возвратить маятник в положение равновесия. Если действием моментов сил трения пренебречь, то из основного уравнения
. Он старается возвратить маятник в положение равновесия. Если действием моментов сил трения пренебречь, то из основного уравнения  динамики вращательного движения достанем
динамики вращательного движения достанем
 , (1)
, (1) и уравнение (1) приобретает вид
и уравнение (1) приобретает вид , (2)
, (2) . (3)
. (3) имеет размерность частоты в квадрате. Тогда период колебаний
имеет размерность частоты в квадрате. Тогда период колебаний . (4)
. (4)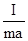 имеет размерность длины, т.е.
имеет размерность длины, т.е. . (5)
. (5) называют приведенной длиной физического маятника. Очевидно, математический маятник будет иметь такой же период колебаний, как и физический маятник, по условиям, которые его длина равняется приведенной длине физического маятника.
называют приведенной длиной физического маятника. Очевидно, математический маятник будет иметь такой же период колебаний, как и физический маятник, по условиям, которые его длина равняется приведенной длине физического маятника. , которая находится на линии ОС на расстоянии l от точки подвеса О, называют точкой колебаний, или центром колебаний физического маятника. Если в этой точке подвесить физический маятник, то его период колебаний не изменится. В самом деле, если
, которая находится на линии ОС на расстоянии l от точки подвеса О, называют точкой колебаний, или центром колебаний физического маятника. Если в этой точке подвесить физический маятник, то его период колебаний не изменится. В самом деле, если  ,
, – момент инерции маятника относительно оси, которая проходит через точку
– момент инерции маятника относительно оси, которая проходит через точку  , а
, а  ,
, – момент инерции маятника относительно параллельной оси, которая проходит через его центр масс. Тогда
– момент инерции маятника относительно параллельной оси, которая проходит через его центр масс. Тогда , а
, а  .
. , то
, то  ;
;  .
.
 . (6)
. (6) Описание установки и методики измерений.
Описание установки и методики измерений. . (7)
. (7) 0) период колебаний Т стремится к бесконечности, т.е. движение становится непериодическим. Период возрастает также при отдалении точки подвеса от центра масс маятника. При некотором определенном значении расстояния а период колебаний является минимальным (Тmin). Если период колебаний отличается от Тmin, то, как видно из рис.3, одно и тоже значение Т достигается при двух разных значениях а. Если поместить точку подвеса на расстоянии а1 от центра тяготения, то центр качания будет находиться на расстоянии а2. Эти значения а1 и а2 и необходимо найти опытным путем, чтобы вычислить g, так как в этом случае
0) период колебаний Т стремится к бесконечности, т.е. движение становится непериодическим. Период возрастает также при отдалении точки подвеса от центра масс маятника. При некотором определенном значении расстояния а период колебаний является минимальным (Тmin). Если период колебаний отличается от Тmin, то, как видно из рис.3, одно и тоже значение Т достигается при двух разных значениях а. Если поместить точку подвеса на расстоянии а1 от центра тяготения, то центр качания будет находиться на расстоянии а2. Эти значения а1 и а2 и необходимо найти опытным путем, чтобы вычислить g, так как в этом случае  является приведенной длиной. Но тяжело достичь совпадения периодов прямого и обратного маятника. Они будут отличаться на какое-то значение
является приведенной длиной. Но тяжело достичь совпадения периодов прямого и обратного маятника. Они будут отличаться на какое-то значение  . Тогда
. Тогда , а
, а  ,
, , то
, то . (8)
. (8) .
. . (9)
. (9) ,т.е., если Т
,т.е., если Т 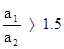 .
.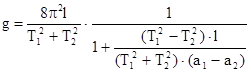 , (10)
, (10)


