
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изучение динамики плоского движения с помощьюСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Маятнике Максвелла
В общем случае положения твердого тела в пространстве можно определить, задав любые три точки этого тела, которые не лежат на одной прямой. Положение каждой из выбранных точек тела относительно некоторой системы отсчета определяется 3-мя координатами
Это означает, что независимых переменных (или степеней свободы), описывающих положение такой системы в пространстве будет всего 5, т.е. любая связь уменьшает число степеней свободы на единицу. Таким образом, твердое тело имеет 6 степеней свободы. Эти шесть независимых параметров можно задавать различными способом в зависимости от обстоятельств.
 Движение твердого тела в пространстве удобно разложить на слагаемые для того, чтобы 3 из 6 параметров описывали поступательное движение тела, а другие 3 ‑ ориентацию тела в пространстве. Для этого достаточно связать жестко с произвольной точкой тела ОБ¢ декартову систему координат Движение твердого тела в пространстве удобно разложить на слагаемые для того, чтобы 3 из 6 параметров описывали поступательное движение тела, а другие 3 ‑ ориентацию тела в пространстве. Для этого достаточно связать жестко с произвольной точкой тела ОБ¢ декартову систему координат  . .
Ориентирование в пространстве этой системы координат, а значит и твердого тела, относительно инерциальной системы отсчета
Положение точки твердого тела Итак, положение твердого тела как системы с шестью степенями свободы описывается шестью параметрами
где Для анализа движения твердого тела, а также условий равновесия необходимо решить систему уравнений движения
Первое уравнение – уравнение движения центра масс тела, второе – уравнение моментов. Для твердого тела эти уравнения являются замкнутой системой, т.е. с их помощью можно полностью определить движение твердого тела в заданных внешних полях, если известны начальные условия. Действительно, для шести неизвестных координат Интересным видом движения является плоское движение, при котором траектории всех точек тела лежат в параллельных плоскостях. Примером плоского движения может служить скатывание шара, цилиндра, обруча по наклонной плоскости. Движение тела в этом случае полностью определяется движением одного из его сечений в какой-нибудь из параллельных плоскостей. Поскольку положение сечения в плоскости определяется заданием координат двух произвольных точек сечения, то при плоском движении тела имеется 3 степени свободы. Уравнения движения (1) и (2) для плоского движения приобретают следующий вид:
 : вектор угловой скорости : вектор угловой скорости  будет всегда перпендикулярен плоскости диска. Поэтому уравнение движения (1¢) и (2¢) можно записать в виде: будет всегда перпендикулярен плоскости диска. Поэтому уравнение движения (1¢) и (2¢) можно записать в виде:
где Для анализа движения маятника систему (3)-(5) удобно решить относительно ускорения
По всей видимости, ускорение диска тем меньше, чем больше момент инерции системы В предлагаемой работе необходимо экспериментально определить зависимость силы натяжения нитей от величины момента инерции системы, воспользовавшись выражением (7). Экспериментальная установка дает возможность изменять момент инерции маятника путем насадки на диск (1) колец, которые имеют разную массу. Для определения момента инерции системы преобразуем выражение (6) к виду
Чтобы экспериментально определить момент инерции маятника
Таким образом, для определения момента инерции системы необходимо определить ее массу Определив момент инерции системы, из выражения (7) легко рассчитать силу натяжения нити Установка позволяет также определить экспериментально моменты инерции использованных в опытах колец. Действительно, измерив время движения
Надев на маятник кольцо массой
Тогда, в силу аддитивности, момент инерции кольца будет равен
Порядок выполнения работы. 1. Измерить штангенциркулем диаметр стержня маятника. 2. Зафиксировать положение центра масс маятника по линейке (3) рис. 2. в верхнем и нижнем положениях маятника и определить путь 3. Поднять маятник в крайнее верхнее положение, наматывая нити виток к витку на стержень и закрепить маятник. 4. Нажать кнопку "Пуск" пульта управления, при этом маятник начинает свое движение и автоматически включается таймер. 5. При прохождении маятником своего нижнего положения таймер автоматически выключается, и на табло пульта управления высвечивается время движения. 6. Нажав кнопку "Сбрасывание", повторить опыт не менее 5 раз. 7. Рассчитать момент инерции маятника 8. Провести эксперименты с разными кольцами, надевая их на диск маятника, в соответстсвии с пунктами 1-7. 9. Результаты экспериментов представить графически в виде зависимости 10. Определить моменты инерции колец, используя выражения (9) и (10). Сравнить с расчетом по формуле 11. Определить погрешности прямых и косвенных измерений.
Контрольные вопросы, задачи 1. Какие параметры определяют положение твердого тела в пространстве? Как определить скорость произвольной точки тела при плоском движении? 2. Является ли система уравнений (1) и (2) замкнутой? 3. Сколько степеней свободы имеет тело, которое осуществляет плоское движение? 4. Выведите соотношения (6) и (7). 5. Определите скорости точек на ободе кольца, лежащих на концах перпендикулярных диаметров в произвольный момент времени. Лабораторная работа № 11 Изучение движения гироскопа Цель работы: ознакомление с особенностями движения гироскопа. Измерение угловой скорости прецессии.
Теоретический материал. Вращательное движение твердого тела. Момент силы. Момент инерции. Момент импульса твердого тела относительно оси. Уравнение моментов. Мгновенные оси вращения. Главные оси и главные моменты инерции, их физическое содержание. Гироскопы и их применение. Прецессия гироскопа. Свободный гироскоп и гироскоп на вращающемся диске. Физический пример прецессии.
 , равно как и вектор угловой скорости , равно как и вектор угловой скорости 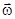 , будет направлен вдоль оси тела. Это понятно из соображений симметрии: в силу осесимметричности движения нет никакого преобладающего направления, куда бы мог быть направлен вектор , будет направлен вдоль оси тела. Это понятно из соображений симметрии: в силу осесимметричности движения нет никакого преобладающего направления, куда бы мог быть направлен вектор  . .
 Чтобы ось фигуры гироскопа могла свободно проворачиваться в пространстве, гироскоп обычно помещают в так называемый карданов подвес (рис. 1). Маховик гироскопа 1 закрепляется на концах диаметра внутреннего кольца 2 (ось СС¢). Внутреннее кольцо, в свою очередь, может вращаться вокруг перпендикулярной оси BB¢, которая проходит через подшипники на концах диаметра внешнего кольца. Наконец, внешнее кольцо 3 может оборачиваться вокруг третьей оси АА¢, проходящей через неподвижный подшипник подставки. Все три взаимно перпендикулярные оси пересекаются в одной точке, которая называется центром карданового подвеса. Гироскоп в кардановом подвесе имеет три степени свободы и может делать любые повороты вокруг центра подвеса и будет уравновешен, если центр его масс совпадает с центром подвеса. До тех пор, пока на гироскоп не действуют никакие внешние силы, его ось будет сохранять свое направление в пространстве в силу закона сохранения момента импульса. Направление (как и величина) вектора Чтобы ось фигуры гироскопа могла свободно проворачиваться в пространстве, гироскоп обычно помещают в так называемый карданов подвес (рис. 1). Маховик гироскопа 1 закрепляется на концах диаметра внутреннего кольца 2 (ось СС¢). Внутреннее кольцо, в свою очередь, может вращаться вокруг перпендикулярной оси BB¢, которая проходит через подшипники на концах диаметра внешнего кольца. Наконец, внешнее кольцо 3 может оборачиваться вокруг третьей оси АА¢, проходящей через неподвижный подшипник подставки. Все три взаимно перпендикулярные оси пересекаются в одной точке, которая называется центром карданового подвеса. Гироскоп в кардановом подвесе имеет три степени свободы и может делать любые повороты вокруг центра подвеса и будет уравновешен, если центр его масс совпадает с центром подвеса. До тех пор, пока на гироскоп не действуют никакие внешние силы, его ось будет сохранять свое направление в пространстве в силу закона сохранения момента импульса. Направление (как и величина) вектора  остается неизменным. Чтобы изменить направление оси гироскопа, необходимо на него подействовать моментом внешних сил. При этом наблюдается противоестественное, на первый взгляд, вращение гироскопа, названное гироскопическим эффектом. Под действием пары сил остается неизменным. Чтобы изменить направление оси гироскопа, необходимо на него подействовать моментом внешних сил. При этом наблюдается противоестественное, на первый взгляд, вращение гироскопа, названное гироскопическим эффектом. Под действием пары сил  и и  (рис. 2), которые казалось бы, должны были вызвать поворот оси гироскопа ОО вокруг прямой ОБ¢ОБ¢ ось гироскопа вращается вокруг прямой ОБ²ОБ² (оси ОО, ОБ¢ОБ¢ и ОБ²ОБ² взаимно перпендикулярны). Этот эффект объясняется законами динамики вращательного движения. Момент пары сил (рис. 2), которые казалось бы, должны были вызвать поворот оси гироскопа ОО вокруг прямой ОБ¢ОБ¢ ось гироскопа вращается вокруг прямой ОБ²ОБ² (оси ОО, ОБ¢ОБ¢ и ОБ²ОБ² взаимно перпендикулярны). Этот эффект объясняется законами динамики вращательного движения. Момент пары сил  в соответствии с определением направлен вдоль прямой ОБ¢ОБ¢. За время в соответствии с определением направлен вдоль прямой ОБ¢ОБ¢. За время 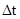 момент импульса момент импульса  , получит приращение , получит приращение
т.е.
 Направление вектора Направление вектора  задает новое положение оси вращения гироскопа и, как легко видеть из рис. 2, ось обернулась вокруг прямой ОБ²ОБ² так, что угол, между векторами задает новое положение оси вращения гироскопа и, как легко видеть из рис. 2, ось обернулась вокруг прямой ОБ²ОБ² так, что угол, между векторами 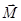 и и  уменьшился. Если действовать на гироскоп продолжительное время внешними силами, которые имеют постоянный по направлению момент уменьшился. Если действовать на гироскоп продолжительное время внешними силами, которые имеют постоянный по направлению момент 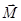 , ось гироскопа установится, в конечном итоге, в направлении, которое совпадает с вектором , ось гироскопа установится, в конечном итоге, в направлении, которое совпадает с вектором 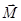 . Это явление положено в основу работы гироскопического компаса. . Это явление положено в основу работы гироскопического компаса.
До сих пор мы рассматривали простое движение гироскопа вокруг оси симметрии. Реальный гироскоп, как правило, принимает участие в более сложном движении, при котором вектор момента импульса
где
Легко заметить, что при
где
В основе теории гироскопов лежит уравнение динамики вращательного движения:
Если момент внешних сил
Из уравнения (4) с учетом того, что моменты инерции
Таким образом, кинетическая энергия вращательного движения гироскопа равно
Совокупность уравнений (3)-(5) позволяет объяснить характер движения гироскопа.
 Устойчивость движения быстро вращающегося гироскопа легко объяснить, исходя из уравнение (3). Действительно, если гироскоп с большим моментом инерции привести в быстрое вращение, то он будет иметь большой момент импульса. Увеличение момента Устойчивость движения быстро вращающегося гироскопа легко объяснить, исходя из уравнение (3). Действительно, если гироскоп с большим моментом инерции привести в быстрое вращение, то он будет иметь большой момент импульса. Увеличение момента  за время за время  определяется формулой (3): определяется формулой (3):
При кратковременных влияниях даже больших сил величина Интересно проявляет себя гироскоп при действии на него внешних сил, момент которых остается постоянным по величине и перпендикулярным к оси обращения. В этом случае наблюдается так называемая вынужденная прецессия гироскопа. Рассмотрим гироскоп, изображенный на рис. 5. Он состоит из маховика 1 и электромотора 2, расположенных на одной оси. Гироскоп устроен так, что он может свободно вращаться вокруг оси симметрии, а также вокруг горизонтальной и вертикальной осей. Приложим к какой-нибудь точке оси гироскопа (т. А) постоянную силу
В таком приближении векторы Направление и величину угловой скорости прецессии легко найти из следующих соображений. Введем единичный вектор
Соответственно избранному направлению вращения маховика векторы
поскольку момент импульса
С учетом (3) получаем:
Принимая во внимание (8), имеем:
 Таким образом, векторы Таким образом, векторы  и и  антипараллельны, причем антипараллельны, причем  имеет размерность частоты (проверить самостоятельно). Эта частота называется частотой прецессии. Гироскоп будет осуществлять вращательное движение вокруг вертикальной оси. Приведенные соображения справедливы при условии имеет размерность частоты (проверить самостоятельно). Эта частота называется частотой прецессии. Гироскоп будет осуществлять вращательное движение вокруг вертикальной оси. Приведенные соображения справедливы при условии  . .
Целью данной работы является ознакомление с особенностями движения гироскопа.
Измерения и обработка результатов. Прибор (рис. 6) состоит из электрического моторчика А, закрепленного в обойме В. Обойма опирается на вертикальный стержень С и может вращаться вокруг горизонтальной оси, а вместе со стержнем ‑ вокруг вертикальной. Углы поворота вокруг этой оси могут определяться по шкале Д. Собственно гироскопом является ротор моторчика с массивным диском Э. Момент внешних сил, приложенных к гироскопу, может изменяться при перемещении груза К по стержню обоймы или дополнительным навесом гирек известной массы. Питание моторчика переменным током осуществляется через автотрансформатор, подводка тока к подвижному моторчику осуществляется через скользящие контакты. В процессе выполнения работы необходимо придерживаться правил безопасности и не притрагиватьс к вращающемуся диску. Перед началом измерений необходимо убедиться в том, что прибор может свободно вращаться вокруг своих осей. Порядок выполнения работы. Ознакомиться с инструкцией по эксплуатации установки. Потом под надзором преподавателя на практике ознакомиться с органами ее управления, которые позволяют задавать и определять: а). момент внешних сил; б). угловую скорость вращения гироскопа; в). угол поворота гироскопа; г). угловую скорость прецессии. Будем базироваться на формуле (10) записав ее в следующем виде:
где: Работа предусматривает выполнение следующего комплекса измерений: а). При фиксированном значении
Из графика следует найти б). При заданной частоте вращения w, снять зависимость W от
Как и раньше определить величину Контрольные вопросы: 1. Что такое оси свободного вращения? Какие из них устойчивы? 2. Что называется гироскопом? 3. Какой гироскоп называется свободным? Уравновешенным? 4. Как устроен карданов подвес? 5. Что такое нутация гироскопа? 6. Что такое прецессия гироскопа? Чем прецессия отличается от нутации? 7. При каких условиях можно считать, что вектор момента импульса гироскопа, мгновенная угловая скорость вращения и ось симметрии совпадают? 8. От чего зависит скорость прецессии? 9. Момент какой силы вызывает прецессию гироскопа в данной работе? Каким способом можно изменять величину и направление момента силы? 10. Что в виду, когда говорят, что прецессия являеться «безынерционным» движением? 11. Почему несвободный гироскоп становится "послушным"? Литература: Физический практикум под редакцией В.И. Ивероновой. Механика и молекулярная физика. -Г., 1967, стр. 133-141. А.Н. Матвеев. Механика и теория относительности. -Г., 1976. §52. С.П. Стрелков. Механика. -Г., 1965, гл. VII, §65, 67. С.Э. Хайкин. Физические основы механики. -Г., 1963, гл. XIII, §103, 104. Колебательные движения Во многих физических явлениях наблюдаются колебательные движения, или колебания. Колебание - это ограниченные движения, которые повторяются, или почти повторяются, относительно некоторого среднего состояния. Это состояние в отдельных случаях может быть состоянием равновесия. Характерной особенностью всех колебательных движений есть их периодичность, т.е. регулярная повторяемость через определенные одинаковые промежутки времени, которые называют периодом колебания. В зависимости от физической природы величины, которая испытывает периодические изменения, различают колебания механические, электромагнитные, и др. Но математические методы их изучения являются общими. Математически одинаково описывается движение маятника настенных часов, движение атомов и ионов в твердом теле возле узлов кристаллической решетки. Подавляющее большинство акустических, электромагнитных и оптических явлений неразрывно связанно с колебательными движениями. Колебательные системы, в которых параметры со временем не изменяются, называют линейными. Колебательные процессы в таких системах достаточно изучены и их математическая теория полностью развита. Колебательные системы, параметры которых зависят от состояния системы, называют нелинейными. Простейшими среди колебательных движений есть гармоничные колебания, при которых физическая величина изменяется со временем по закону синуса или косинуса. Гармоничные колебания важны тем, что все колебания, которые встречаются в природе и технике, с довольно добрым приближением описываются синусоидальным законом. Даже тогда, когда колебания происходят несинусоидально, их можно представить как результаты наложения нескольких гармоничных колебаний. Общий подход к изучению колебательных процессов был впервые сформулирован Л.И.Мандельштамом. Фундаментальный вклад у изучение колебаний внесли Ж.Лагранж, А.Пуанкаре, Дж.Максвелл, Г.Герц., А.М.Ляпунов, О.М.Крылов, А.А.Андронов, Г.С.Горелик, М.В.Келдыш и др. РАБОТА №12
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 963; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.016 с.) |

 Таким образом, общее число координат, которые описывают положение твердого тела, равняется 9. Однако, не все из этих девяти координат будут независимыми. Так как в твердом теле расстояние между любыми произвольными точками тела в процессе его движения не меняется, то независимых параметров останется шесть. Действительно, положение двух точек в пространстве характеризуется 6-ю координатами:
Таким образом, общее число координат, которые описывают положение твердого тела, равняется 9. Однако, не все из этих девяти координат будут независимыми. Так как в твердом теле расстояние между любыми произвольными точками тела в процессе его движения не меняется, то независимых параметров останется шесть. Действительно, положение двух точек в пространстве характеризуется 6-ю координатами:  для одной точки и
для одной точки и  ‑ для другой. Если между этими точками существует твердая связь, например, они соединены между собой стрежнем длиной
‑ для другой. Если между этими точками существует твердая связь, например, они соединены между собой стрежнем длиной  , то каждая из координат может быть найдена из очевидного соотношения
, то каждая из координат может быть найдена из очевидного соотношения
 , в которой рассматривается движение тела, полностью определяется углами Эйлера
, в которой рассматривается движение тела, полностью определяется углами Эйлера 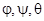 (рис. 1). Эти углы фиксируются таким образом: выбирается линия узлов ОА – линия сечения плоскостей
(рис. 1). Эти углы фиксируются таким образом: выбирается линия узлов ОА – линия сечения плоскостей 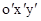 и
и  . Тогда указанные на рисунке углы
. Тогда указанные на рисунке углы 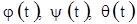
 , с которой связана система координат
, с которой связана система координат  этой точки относительно инерциальной системы координат или же декартовыми координатами
этой точки относительно инерциальной системы координат или же декартовыми координатами  .
.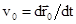 точки твердого тела О и вращательного движения с мгновенной угловой скоростью
точки твердого тела О и вращательного движения с мгновенной угловой скоростью  ,
, ‑ радиус-вектор произвольной точки твердого тела в системе
‑ радиус-вектор произвольной точки твердого тела в системе  (1)
(1) (2)
(2) (1¢)
(1¢) (2¢)
(2¢)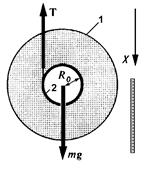 Здесь w и M ‑ проекция векторов
Здесь w и M ‑ проекция векторов  (3)
(3) (4)
(4) (5)
(5) - радиус стрежня,
- радиус стрежня,  - момент инерции системы относительно оси вращения,
- момент инерции системы относительно оси вращения, 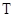 - сила натяжения нитей.
- сила натяжения нитей. и силы натяжения
и силы натяжения  . После нескладных преобразований получаем:
. После нескладных преобразований получаем: (6)
(6) (7)
(7) ускорение диска
ускорение диска  , а сила натяжения
, а сила натяжения  . В этом случае диск будет просто неподвижно висеть на нитях. При
. В этом случае диск будет просто неподвижно висеть на нитях. При  , т.е. диск будет свободно падать и потому нити не испытают никакого натяжения. Уравнения (3) и (4) не описывают поведение маятника в нижний мертвой точке, когда происходит перебрасывание нитей с одной стороны стержня на другую. Диск будет продолжать вращаться в прежнем направлении, но нити будут уже наматываться на стержень, так что диск придет в движение вверх, пока его кинетическая энергия не превратиться в потенциальную. Следует отметить, что в нижний мертвой точке происходит изменение направления скорости на обратную. Поэтому в этот момент центр масс маятника испытает большее ускорение, что приводит к большому натяжению нитей.
, т.е. диск будет свободно падать и потому нити не испытают никакого натяжения. Уравнения (3) и (4) не описывают поведение маятника в нижний мертвой точке, когда происходит перебрасывание нитей с одной стороны стержня на другую. Диск будет продолжать вращаться в прежнем направлении, но нити будут уже наматываться на стержень, так что диск придет в движение вверх, пока его кинетическая энергия не превратиться в потенциальную. Следует отметить, что в нижний мертвой точке происходит изменение направления скорости на обратную. Поэтому в этот момент центр масс маятника испытает большее ускорение, что приводит к большому натяжению нитей. .
.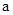 . Ускорение системы легко определить из выражения
. Ускорение системы легко определить из выражения  , где
, где  - расстояние, которое проходит центр масс маятника;
- расстояние, которое проходит центр масс маятника;  - время движения. Тогда последнее выражение можно переписать
- время движения. Тогда последнее выражение можно переписать (8)
(8) , измерить радиус стержня
, измерить радиус стержня 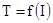 .
. маятника с высоты
маятника с высоты  , по формуле (8) можно рассчитать момент инерции маятника
, по формуле (8) можно рассчитать момент инерции маятника  .
. (9)
(9) , и повторив опыт, найдем момент инерции системы маятник-кольцо:
, и повторив опыт, найдем момент инерции системы маятник-кольцо: (10)
(10) . Отметим, что в опытах высоты
. Отметим, что в опытах высоты  .
. .
. Элементарные сведения о гироскопах
Элементарные сведения о гироскопах , (1)
, (1)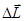 параллельно
параллельно  .
. . Рассмотрим частный случай движения тела, у которого закреплена одна точка (т. ОБ, рис. 3). Положим, что гироскоп вращается с угловой скоростью
. Рассмотрим частный случай движения тела, у которого закреплена одна точка (т. ОБ, рис. 3). Положим, что гироскоп вращается с угловой скоростью  вокруг оси ОО и одновременно ось ОО вращается вокруг оси ОО¢ с угловой скоростью
вокруг оси ОО и одновременно ось ОО вращается вокруг оси ОО¢ с угловой скоростью  . Это движение можно заменить вращением с угловой скоростью
. Это движение можно заменить вращением с угловой скоростью  вокруг мгновенной оси, положение которой определяется вектором
вокруг мгновенной оси, положение которой определяется вектором  ;
;  ,
, и
и  - моменты инерции относительно осей ОО и ОО¢. Тогда вектор
- моменты инерции относительно осей ОО и ОО¢. Тогда вектор  .
. ¹
¹ 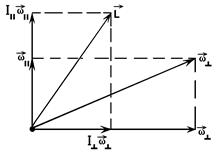 К аналогичному результату можно прийти, если рассмотреть вращение гироскопа вокруг мгновенной оси, которая не совпадает с осью симметрии (см. рис. 4). В этом случае можно разложить вектор
К аналогичному результату можно прийти, если рассмотреть вращение гироскопа вокруг мгновенной оси, которая не совпадает с осью симметрии (см. рис. 4). В этом случае можно разложить вектор  и перпендикулярную к ней
и перпендикулярную к ней  . В результате получаем:
. В результате получаем: , (2)
, (2) и
и  - моменты инерции относительно указанных осей. (Очевидно, что направление
- моменты инерции относительно указанных осей. (Очевидно, что направление  . (3)
. (3) =
=  (4)
(4) и
и  вектора
вектора  :
:
 (5)
(5) .
. , и направление оси гироскопа практически не изменяется. Гироскоп как бы сопротивляется всяким попыткам изменить величину и направление его момента импульса.
, и направление оси гироскопа практически не изменяется. Гироскоп как бы сопротивляется всяким попыткам изменить величину и направление его момента импульса. (6)
(6) параллельны (рис. 4). Поскольку момент силы
параллельны (рис. 4). Поскольку момент силы  , направленный вдоль оси гироскопа. Длину отрезка ОА обозначим буквой
, направленный вдоль оси гироскопа. Длину отрезка ОА обозначим буквой  . Тогда момент силы
. Тогда момент силы  , так как
, так как  (7)
(7) ,
,  (8)
(8) взаимно перпендикулярны и не изменяются по модулю, их можно связать соотношением:
взаимно перпендикулярны и не изменяются по модулю, их можно связать соотношением: (9)
(9)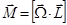
 откуда
откуда  и.
и. (10)
(10)
 , (11)
, (11) снять зависимость угловой скорости прецессии W от угловой скорости обращения гироскопа w. Построить график в переменных
снять зависимость угловой скорости прецессии W от угловой скорости обращения гироскопа w. Построить график в переменных  , представляющий собой прямую, тангенс угла наклона которой к оси абсцисс равняется:
, представляющий собой прямую, тангенс угла наклона которой к оси абсцисс равняется: .
. и по известным величинам
и по известным величинам  ,
,  относительно оси симметрии.
относительно оси симметрии. , потом определить тангенс угла наклона прямой к оси абсцисс. В этом случае его величина определяется выражением:
, потом определить тангенс угла наклона прямой к оси абсцисс. В этом случае его величина определяется выражением: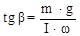 .
.


