
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В проекции на вертикальную осьСодержание книги
Поиск на нашем сайте
Пренебрегая трением в блоке и его массой, можно считать, что Поскольку нить есть нерастяжимой, то
С помощью машины Атвуда можно исследовать законы равномерного движения без начальной скорости:
На правом грузе размещают перегрузок 7 массой m, а левый груз удерживают электромагнитом. В момент выключения электромагнита включается секундомер, а в момент удара груза об сплошную платформу 4 секундомер выключается. Изменяя положение платформы 4, убедиться в справедливости формулы (4). Для определения скорости, в данный момент времени следует в тот же момент прекратить действие перегрузка 8 и дать возможность грузам двигаться по инерции. Устранение перегрузка 8 производится с помощью подставки 6. Для определения скорости измеряют время t от начала движения грузов до момента снятия перегрузка, а также время
Эта скорость равняется мгновенной скорости равнопеременного движения в момент времени
Изменяя расстояние от фиксированного положения правого груза на подставке 6, меняют скорость Для проверки второго закона Ньютона
Где Порядок выполнения работы: 1. Проверьте формулу (4) для пути при равнопеременном движении. При неизменной массе перегрузка проведите не меньше пяти опытов, изменяя величину
Таблица 1
Постройте график зависимости 2. Проверьте формулу (5) для скорости равнопеременного движения. Для этого оставьте массу перегрузка неизменной, таким образом и ускорение останется постоянным. Изменяя расстояние между фиксированным положением правого груза и подставкой 6, которая снимает перегрузок 8, меняют мгновенную скорость. Опыт проводят для пяти разных положений подставки 6. Результаты экспериментов и расчетов
Таблица 2
Строят графики зависимости 3. Проверьте выполнение второго закона Ньютона Таблица 3
Проводят сравнение полученного среднего значения
Контрольные вопросы: 1. Сформулируйте законы динамики поступательного движения. 2. Какой вид имеет график зависимости координаты от времени при равнопеременном движении при наличии начальной скорости и при ее отсутствии? Как по этому графику определить скорость тела в данный момент времени? 3. Равнопеременное движение тел можно было бы изучать на примере свободного падения. Которые при этом возникают трудности? В чем преимущество и недостатки изучения такого характера движения с помощью машины Атвуда? 4. Какие ошибки возникают в данной работе? Какие мероприятия следует принять для их устранения или для уменьшения величины этих ошибок? 5. Изменяется ли натяжение нитей, если один груз заменить другим?
Рекомендованная литература: 1. Инструкция. 2. Д.В. Сивухин, Общий курс физики. I, -М., 1974, § 11, 12. 3. С.П.Стрелков,Общий курс физики. Механика, -М.,1975,§16, 17.
Лабораторная работа № 4 ДВИЖЕНИЕ ЦЕНТРА МАСС СИСТЕМЫ Цель работы: проверка законов динамики материальной точки, получение навыков построения графиков и учета систематических ошибок. Теоретический материал. Определение материальной точки. Описание перемещения, скорости и ускорение материальной точки в векторной и координатной форме. Прямолинейное движение материальной точки. Физическое содержание I закона Ньютона. Сила как мера интенсивности взаимодействия тел. Второй закон Ньютона. Масса. Импульс. III закон Ньютона.
В любой системе материальных тел есть одна замечательная точка С – центр инерции или центр масс, которая имеет ряд интересных и важных свойств. Определим положение этой точки относительно начала О данной системы отсчета радиус-вектором
где В проекциях на координатные оси:
В случае однородного твердого тела, который имеет центр симметрии, центр масс совпадает с центром симметрии. Если тело имеет ось симметрии, то центр масс лежит на этой оси. В более сложных случаях координаты центра масс находятся или путем расчетов, или экспериментально. Отметим также, что в однородном поле силы тяжести центр инерции системы совпадает с ее центром тяжести. Найдем скорость движения центра масс. Взяв производную от (1) по времени, получим
где Для импульса системы
т.е. импульс системы равняется произведению массы системы на скорость движения ее центра масс. Учитываем, что
где
Уравнение (5) называется уравнением движения центра масс. Согласно этому уравнению, при движении любой системы тел (в инерциальной системе отсчета), ее центр масс двигается так, как если бы вся масса системы была сосредоточена в этой точке и к ней были бы приложенны все внешние силы, которые действуют на систему. При этом ускорение центра масс совершенно не зависит от точек приложения внешних сил.
Целью данной работы является экспериментальная проверка теоремы о движении центра масс. Для этого используется машина Атвуда, дополненная некоторыми деталями. Два грузика А и В (см.рис.1), массы которых одинаковы и равны 0,5 кг, висят на двух параллельных нитях, перекинутых через блоки С и Д. Использование двух параллельных нитей не дает возможности грузикам вращаться вокруг их вертикальных осей. Грузик А имеет форму цилиндра, Грузик В состоит из двух полуцилиндров, составленных своими плоскостями так, что между ними существует щель. Центр масс этого грузика находится на тонком проводе, который соединяет две его половины. Приблизительно на середине прямой, соединяющей центры масс свободно висящих грузиков, размещен рычаг Р, который может вращаться в вертикальной плоскости вокруг оси О и перемещаться поступательно в плоскости обращения. Это позволяет выставить острый конец рычага Р в центре масс грузиков А и В и зафиксировать такое положение рычага зажимным винтом. К острому конца рычага прикреплена нить Z. Она проходит в щель рычага В через его центр масс (нить перекинута через провод в щели) и опускается вертикальную вниз между двумя полуцилиндрами. Она все время натянута, поскольку на ее нижнем конце закреплен грузик Е. На грузике В симметрично с двух его концов прикрепленны крючки (на рис. 1 не указаны), на которые можно подвешивать дополнительный груз. При нагрузке дополнительными грузиками (массой грузика Е пренебрегаем) центр масс системы смещается вдоль нити Z (ось Х). Когда система двигается (грузик В ‑ вертикально вверх, грузик А ‑ вертикально вниз), центр масс двигается вниз вдоль оси Y, оставаясь все время на линии натянутой нити. Итак, за движущимся центром масс можно следить как за движением определенной и фиксированной точки пересечения нити Z и вертикальной прямой Y. Этой прямой является левый край металлической линейки R с делениями, способной перемещаться параллельно самой себе в вертикальной плоскости. Перемещение линейки достигается тем, что она свободно подвешена к краю диска С, который может вращаться вокруг горизонтальной оси О. Вращение диска по часовой стрелке дает перемещение линейки вправо и наоборот. Зажимным винтом диск, а значит и линейка могут быть закрепленны в нужном положении. Для удержания грузиков (при наличии дополнительного груза на грузике В) в покое используется электромагнит N. Включенный электромагнит удерживает грузик. При размыкании ключа электромагнит отключается и включается электросекундомер, который фиксирует начало движения. Время движения определяется по электросекундомеру, который останавливается в тот момент, когда грузик В достигает нижней платформы, на которой имеется электрический контакт для выключения секундомера. В условиях данной задачи, х - координата центра масс остается неизменной и равной
где
Y-компонента центра масс двигается вдоль вертикали, которая совпадает с левым краем линейки R, с ускорением которое может быть найдено из уравнения движения центра масс (5). Оно в данной ситуации имеет вид
Здесь Уравнение движения для грузиков В и А (пренебрегая силами их трения в воздухе) имеют вид
Здесь Из уравнений (8) и (9) получим
Пренебрегая массой блоков С и П по сравнению с массой грузиков А и В можно разность
где
Из уравнений (7), (8), (9) получим
Подставив (12) в (13), окончательно имеем
Порядок выполнения работы 1. Прежде чем начать измерение, необходимо убедиться, что нити не перекручены (грузики легко двигаются), электромагнит функционирует и при опускании грузика В замыкается контакт, который выключает электросекундомер. 2. На грузик В навешивают дополнительные грузики и находят, при каком наименьшем 3. Потом к грузику В добавляют еще дополнительные грузики (10 или 15 г) и определяют из формулы (6) 4. После этого грузик В поднимают и фиксируют на заданной высоте, включив ток в цепи электромагнита. Отмечают то деление на вертикальной линейке, напротив которого проходит натянутая нить Z. Выключают ток в цепи электромагнита, одновременно включают электросекундомер. В момент удара грузика В о нижнюю платформу секундомер прекращает отсчет времени движения. Записывают показание секундомера. Отмечают, на каком отсчете шкалы линейки находилась в этот момент нить. Это дает возможность определить расстояние, которое проходит центр масс за известное время. Это время можно изменять, меняя положение нижней платформы на стойке. Для заданной величины перегрузки на грузик В и разных интервалов движения грузиков (разных положений платформы) ускорение должно оставаться постоянной величиной. 5. Для определения величины ускорения перемещения центра масс используется кинематическое соотношение
где 6. Непосредственная проверка теоремы о движении центра масс состоит в соответствии (в пределах погрешности измерений) определенной опытным путем величины и рассчитанной по формуле (14).
Контрольные вопросы: 6. Сформулируйте законы динамики поступательного движения. 7. Какой вид имеет график зависимости координаты от времени при равнопеременном движении при наличии начальной скорости и при ее отсутствии? Как по этому графику определить скорость тела в данный момент времени? 8. Равнопеременное движение тел можно было бы изучать на примере свободного падения. Какие при этом возникают трудности? В чем преимущество и недостатки изучения такого характера движения с помощью машины Атвуда? 9. Какие ошибки возникают в данной работе? Какие меры следует предпринять для их устранения или для уменьшения величины этих ошибок? 10. Изменяется ли натяжение нитей, если один грузик заменить другим?
Рекомендованная литература: 4. Инструкция. 5. Д.В. Сивухин, Общий курс физики. I, -М., 1974, § 11, 12. 6. С. П. Стрелков,Общий курс физики. Механика,-М.,1975,§16, 17.
Лабораторная работа № 5
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 581; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.37.178 (0.011 с.) |

 . (2)
. (2) . Из третьего закона Ньютона следует
. Из третьего закона Ньютона следует  .
. , тогда из (2) получаем:
, тогда из (2) получаем: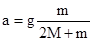 . (3)
. (3)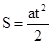 , (4)
, (4) . (5)
. (5) от момента снятия перегрузка до момента столкновения правого груза со сплошной платформой 4. Зная расстояние между платформами 6 и 4, находят скорость равномерного движения между платформами
от момента снятия перегрузка до момента столкновения правого груза со сплошной платформой 4. Зная расстояние между платформами 6 и 4, находят скорость равномерного движения между платформами . (6)
. (6)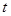 снятия перегрузка 8, т.е.:
снятия перегрузка 8, т.е.: . (7)
. (7) равномерного движения и убеждаются в справедливости формулы (5).
равномерного движения и убеждаются в справедливости формулы (5). действуют таким образом: на оба груза помещают разные перегрузки и определяют ускорение
действуют таким образом: на оба груза помещают разные перегрузки и определяют ускорение  . После этого оба перегрузка помещают на одно тело, т.е. увеличивают результирующую силу при неизменной общей массе, и определяют ускорение
. После этого оба перегрузка помещают на одно тело, т.е. увеличивают результирующую силу при неизменной общей массе, и определяют ускорение  . Согласно второму закону Ньютона
. Согласно второму закону Ньютона  находят отношение ускорений
находят отношение ускорений , (8)
, (8) и
и  – массы перегрузков. Изменяя эти массы, убеждаются в справедливости формулы (8), которая является следствием второго закона динамики.
– массы перегрузков. Изменяя эти массы, убеждаются в справедливости формулы (8), которая является следствием второго закона динамики. и измеряя
и измеряя 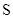


 от
от  . Обязательно укажите погрешности для каждой точки. По графику определите ускорение. Полученное значение сравните с величиной, рассчитанной по формуле (3).
. Обязательно укажите погрешности для каждой точки. По графику определите ускорение. Полученное значение сравните с величиной, рассчитанной по формуле (3). заносят в таблицу 2 (величины
заносят в таблицу 2 (величины 


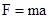 . Для этого размещают на правом грузе перегрузок большей массы 8, а на левом – меньшей массы (типа 7). Выключая электромагнит измеряют время
. Для этого размещают на правом грузе перегрузок большей массы 8, а на левом – меньшей массы (типа 7). Выключая электромагнит измеряют время  также как среднее трех измерений. Результат эксперимента
также как среднее трех измерений. Результат эксперимента  и расчетов
и расчетов  заносят в таблицу 3 для пяти разных положений платформы 4.
заносят в таблицу 3 для пяти разных положений платформы 4.

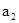
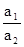
 с величиной
с величиной  .
.
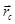 таким образом:
таким образом: , (1)
, (1) и
и  – масса и радиус-вектор і-го тела,
– масса и радиус-вектор і-го тела,  - масса всей системы.
- масса всей системы. ,
, 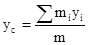 ,
,  . (1a)
. (1a) , (2)
, (2) - импульс
- импульс  -го тела.
-го тела. , из (2) будем иметь:
, из (2) будем иметь: , (3)
, (3)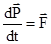 , (4)
, (4) – результирующая всех внешних сил, которые действуют на систему. Из (2) и (4) получим
– результирующая всех внешних сил, которые действуют на систему. Из (2) и (4) получим . (5)
. (5)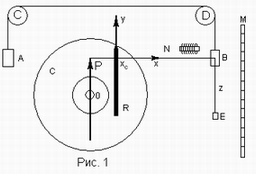 Из (5)следует, что когда
Из (5)следует, что когда  , то
, то  , ведь
, ведь 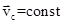 .Таким, в частности, является случай замкнутой системы. Кроме того, если
.Таким, в частности, является случай замкнутой системы. Кроме того, если  , то, согласно (3), импульс системы также является константой. Т.е., если центр масс системы двигается равномерно и прямолинейно, то ее импульс сохраняется в процессе движения. Уравнение (5) по форме совпадает с основным уравнением динамики материальной точки и является его обобщением на случай системы тел.
, то, согласно (3), импульс системы также является константой. Т.е., если центр масс системы двигается равномерно и прямолинейно, то ее импульс сохраняется в процессе движения. Уравнение (5) по форме совпадает с основным уравнением динамики материальной точки и является его обобщением на случай системы тел. , (6)
, (6)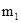 – масса грузика В и всех дополнительных грузиков на нем;
– масса грузика В и всех дополнительных грузиков на нем; - масса грузика А;
- масса грузика А; и
и  – их горизонтальные координаты, которые отсчитываются от конца рычага Р.
– их горизонтальные координаты, которые отсчитываются от конца рычага Р. . (7)
. (7)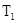 и
и  ‑ натяжение нитей грузиков В и А соответственно.
‑ натяжение нитей грузиков В и А соответственно.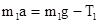 , (8)
, (8) . (9)
. (9)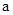 – ускорение движениягрузиков, нить считаем невесомой и нерастяжимой, за положительное направление принято направление вектора
– ускорение движениягрузиков, нить считаем невесомой и нерастяжимой, за положительное направление принято направление вектора  .
. . (10)
. (10) отождествить с силой трения в осях двух блоков, т.е. считать
отождествить с силой трения в осях двух блоков, т.е. считать , (11)
, (11) – масса дополнительного тягарця при определении силы трения (см. ниже). С учетом (11), формула (10) принимает вид
– масса дополнительного тягарця при определении силы трения (см. ниже). С учетом (11), формула (10) принимает вид . (12)
. (12) . (13)
. (13) . (14)
. (14) – координату центра масс. Начало координат при этом следует поместить в центр масс грузиков А и В (без учета дополнительных грузов), т.е. в месте закрепления нити Е. В этом случае координаты
– координату центра масс. Начало координат при этом следует поместить в центр масс грузиков А и В (без учета дополнительных грузов), т.е. в месте закрепления нити Е. В этом случае координаты  центров масс грузиков А и В равны по модулю и могут быть найденны как половина расстояния между грузами А і В, когда они находятся на одном уровне (
центров масс грузиков А и В равны по модулю и могут быть найденны как половина расстояния между грузами А і В, когда они находятся на одном уровне ( ). Определив величину расстояния
). Определив величину расстояния 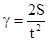 ,
, – расстояние,
– расстояние, 


