
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение модулей упругости растягивания и изгибаСодержание книги
Поиск на нашем сайте
Цель работы: определение модуля Юнга из растягивание провода и из изгиба балки, ознакомление с методами измерения модуля Юнга Теоретический материал. Упругие силы. Деформация сплошной среды. Типы упругих деформаций. Связь между силой и деформацией. Закон Гука для деформаций растягивания и сдвига. Модуль Юнга. Коэффициент Пуассона. Энергия упругой деформации. Диаграмма растягивания. Хрупкость и пластичность. Определение модуля Юнга из растягивание провода. Рассмотрим один из простейших случаев упругой деформации - растягивание провода, который имеет постоянное сечение S. Верхний Соответственно закону Гука, относительное удлинение
Коэффициент пропорциональности α в формуле (1) записанный как Из соотношения (1) видно, что модуль Юнга равняется такому напряжению, которое растянуло бы тело цилиндрической формы вдвое ( Формула (1) является рабочей при измерении величины Е методом растяжения. Принимая во внимание соотношение
Обратимся теперь к методике измерений и обработки результатов эксперимента. Блок-схема экспериментальной установки представлена на рис. 1. К стальному проводу (KL) прикрепленная платформа (А), на которую последовательно кладут грузы. С помощью индикатора (В) определяется абсолютное удлинение Задача 1. Измерения
Задача 2. Одна из задач экспериментальной физики заключается в проверке связей между определенными физическими величинами, которые предусмотрены теорией. Подобные эксперименты позволяют, в частности, проявить качество теоретической модели, установить границы (условия) ее применение, определить численные величины параметров, которые входят в аналитические выражения. Одним из методов, которые разрешают наиболее точно определить указанные параметры по результатам измерений, есть метод наименьших квадратов. Коротко напомним его содержание относительно нашей работы. Итак, мы знаем, что абсолютное удлинение провода Δl должно быть прямо пропорционально массе груза m, т.е.
где коэффициент пропорциональности К, как это видно из формулы (1), равняется:
Иначе говоря, экспериментальные точки в переменных (
Минимум суммы S(K) ищется по правилам дифференциального исчисления и условия:
Таким образом, по данным измерений можно найти (К), а потом, соответственно соотношению (4), и модуль Юнга. Нанесите экспериментальные точки на график
Определение модуля Юнга из изгиба балки (пластины) прямоугольной формы.
Если горизонтально расположенную упругую балку (пластину) закрепить с одного конца, а другой конец нагрузить телом весом Перемещение λ, которое получает свободный конец пластины, называется стрелой прогиба. Стрела прогиба будет зависеть от модуля Юнга (Е) и геометрических параметров пластины. Для пластины, которая имеет длину (L), ширину (а) и высоту (b), стрела прогиба выражается формулой:
В случае, если пластина будет обеими концами свободно положенная на твердые сопротивления и нагруженная в середине весом
Формула (8) разрешает определить модуль Юнга соответственно методикам, описанным выше, что и предлагается выполнить студентам. Установка для определения модуля упругости по величине изгиба состоит из массивной платформы с двумя стойками на концах. На стойках укрепленные стальные призмы так, что ребра их параллельные между собой. На специальной штанге укрепляют индикатор так, чтобы штифт касался середины внутренней плоскости пластины. Сверху на середину пластины нагружают последовательно 0.5 кг, 1 кг, 1.5 кг, 2 кг, 2.5 кг, каждый раз определяя стрелу прогиба с помощью индикатора. Дальше проделывают ту же операцию в обратном порядке, отмечая каждый раз ее прогиб. Результаты заносятся в таблицу. Определите модуль Юнга используя методики, предложенные выше. Оцените погрешности измерений соответственно соотношению:
где Контрольные вопросы: 1. По какому признаку тела делятся на упругие и неупругие? Что называется деформацией тела? Какая особенность сил, которые возникают внутри тела при упругих и пластических деформациях? В чем причина упругих и пластических деформаций? 2. Как по величине внешней силы, которая деформирует тело, определить возникающую при этом силу упругости? 3. Перечислите основные типы деформаций. 4. Что называется деформацией растяжения (сжатия), сдвига? Как при этом смещаются отдельные пласты (и частицы) тела? Какими абсолютными и относительными величинами характеризуются эти деформации и какими силами они вызываются? 5. Что такое механическое напряжение, и в каких единицах она измеряется? 6. В чем заключается закон Гука? Как он математически записывается в общей форме? Приведите запись закона Гука для деформации растяжения и сдвига. 7. Что называют модулем Юнга и модулем сдвига? Какими единицами они измеряются и как они связаны с коэффициентами растяжения и сдвига? 8. Изобразите образец графика зависимости упругого напряжения от значения деформации. Укажите область пластических деформаций. 9. Что называют границей пропорциональной зависимости? Границей упругости? Границей прочности? 10. Что называется коэффициентом Пуассона? 11. Которые из величин в данных роботах необходимо измерить точнее и чему? 12. Как деформируются отдельные пласты стержня при его изгибе? Что называется стрелой прогиба? 13. С какой целью рекомендуется делать измерения как при возрастающих, так и при ниспадающих нагрузках? 14. Каким образом можно исключить влияние начального изгиба провода на точность определения Е? 15. Что необходимо начать, чтобы в процессе эксперимента не выйти за пределы области где удлинение провода пропорционально ее натяжения (область пропорциональности)?
Рекомендованная литература: 1. Физический практикум под редакцией В.И. Ивероновой, Механика и молекулярная физика, -М., 1967 2. С.П. Стрелков. Механика, -М., Наука. 1965. гл, X, §81-84, 86-89. 3. С.Э. Хайкин. Физические основы механики, -М., 1963, гл XIV. §105-106 4. И.В. Савельев. Курс общей физики, т. I. Механика, колебание и волны, молекулярная физика, -М., 1973, §45.
Лабораторная работа №3 Изучение второго закона динамики на машине Атвуда Цель работы: проверка законов динамики материальной точки, приобретение навыков построения графиков и учет систематических ошибок.
Теоретический материал. Определение материальной точки. Описание перемещения, скорости и ускорение материальной точки в векторной и координатной формах. Прямолинейное движение материальной точки. Физическое содержание I закона Ньютона. Сила как мера интенсивности взаимодействия тел. Второй закон Ньютона. Масса. Импульс. III закон Ньютона.
Если на правый груз поместить дополнительный перегрузок массой m и отключить электромагнит, то система придет в движение. Для В векторной форме
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 642; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.217.1 (0.009 с.) |

 конец провода закрепим, а к нижнему подвесим груз с массой m. Пусть l0- начальная длина провода,
конец провода закрепим, а к нижнему подвесим груз с массой m. Пусть l0- начальная длина провода, 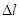 -ее абсолютное удлинение под действием груза m.
-ее абсолютное удлинение под действием груза m.
 будет прямо пропорционально нормальному напряжению σ (
будет прямо пропорционально нормальному напряжению σ ( ). В нашем случае
). В нашем случае  (g-ускорение свободного падения). Таким образом, можно записать:
(g-ускорение свободного падения). Таким образом, можно записать: . (1)
. (1) . Константа Е характеризует упругие свойства тела и называется модулем Юнга. Легко видеть, что размерность последнего в системе СИ
. Константа Е характеризует упругие свойства тела и называется модулем Юнга. Легко видеть, что размерность последнего в системе СИ 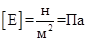 .
. ). Однако, для большинства тел это невозможно, так как они разрываются раньше.
). Однако, для большинства тел это невозможно, так как они разрываются раньше.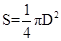 , получаем
, получаем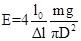 . (2)
. (2) не является величиной постоянной, как это выходит формально из формулы (2). Действительно, все величины, которые входят в (2), за исключением
не является величиной постоянной, как это выходит формально из формулы (2). Действительно, все величины, которые входят в (2), за исключением 

 , (3)
, (3) . (4)
. (4) ,
,  ) должны укладываться на прямую. Однако, из-за погрешности измерений это будет не так. Точки, действительно, будут ложиться более или менее на прямую, но как ее провести? Быть может, на глаз? Уравнение искомой прямой (3) нам известно, но не известна величина константы К. Обычно в уравнение прямой прибавляют также и свободный член (С), что разрешает лучше уложить точки на прямую. Он связан с какими-нибудь систематическими погрешностями. Будем считать, что мы их учли, поэтому
) должны укладываться на прямую. Однако, из-за погрешности измерений это будет не так. Точки, действительно, будут ложиться более или менее на прямую, но как ее провести? Быть может, на глаз? Уравнение искомой прямой (3) нам известно, но не известна величина константы К. Обычно в уравнение прямой прибавляют также и свободный член (С), что разрешает лучше уложить точки на прямую. Он связан с какими-нибудь систематическими погрешностями. Будем считать, что мы их учли, поэтому  . Таким образом, каждому значению mi мы можем сопоставить два значения абсолютного удлинения провода
. Таким образом, каждому значению mi мы можем сопоставить два значения абсолютного удлинения провода  . Одно из них получено в результате измерений
. Одно из них получено в результате измерений  . Обычно последнее мы не знаем, так как коэффициент К заранее не известен. Тем не менее, введем разность
. Обычно последнее мы не знаем, так как коэффициент К заранее не известен. Тем не менее, введем разность  , которая показывает отклонение результатов измерений от теоретических значений. Константу (К), соответственно методу наименьших квадратов, находят из условия минимума суммы квадратов отклонений:
, которая показывает отклонение результатов измерений от теоретических значений. Константу (К), соответственно методу наименьших квадратов, находят из условия минимума суммы квадратов отклонений: . (5)
. (5) . Дифференцируя (5), получаем:
. Дифференцируя (5), получаем: . (6)
. (6) , то этот конец опустится, т.е. пластина деформируется. Легко понять, что при таком изгибе верхние пласты пластины будут растягиваться, нижние - сжиматься, а некоторый средний (нейтральный) пласт сохраняет длину и только претерпевает искривление.
, то этот конец опустится, т.е. пластина деформируется. Легко понять, что при таком изгибе верхние пласты пластины будут растягиваться, нижние - сжиматься, а некоторый средний (нейтральный) пласт сохраняет длину и только претерпевает искривление. . (7)
. (7) (рис. 2), стрела прогиба будет также определяться формулой (7), но с заменой Р на
(рис. 2), стрела прогиба будет также определяться формулой (7), но с заменой Р на  и
и 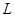 на
на  . Действительно, в случае такого изгиба каждая из опор совершает на пластину противодействую, равную
. Действительно, в случае такого изгиба каждая из опор совершает на пластину противодействую, равную 
 . (8)
. (8)
 .
. Машина Атвуда состоит из легкого блока 1, закрепленного на верхнем конце вертикальной штанги 2, на которой нанесена шкала с сантиметровыми пометками. Блок вращается с достаточно малым трением, иначе необходимо предусматривать компенсацию этого трения. Через блок перекинута нить с двумя одинаковыми грузами массой М. Грузи могут опираться на подставки 4, а также способны перемещаться вдоль штанги. Для фиксации грузов в заданном положении и для их освобождения используется электромагнит 5. Подставки 4 - сплошные, подставка 6 имеет отверстие, через которое свободно проходит груз. Кроме того в комплект входят дополнительные грузи 7 и 8, которые используют для приведения системы в состояние движения.
Машина Атвуда состоит из легкого блока 1, закрепленного на верхнем конце вертикальной штанги 2, на которой нанесена шкала с сантиметровыми пометками. Блок вращается с достаточно малым трением, иначе необходимо предусматривать компенсацию этого трения. Через блок перекинута нить с двумя одинаковыми грузами массой М. Грузи могут опираться на подставки 4, а также способны перемещаться вдоль штанги. Для фиксации грузов в заданном положении и для их освобождения используется электромагнит 5. Подставки 4 - сплошные, подставка 6 имеет отверстие, через которое свободно проходит груз. Кроме того в комплект входят дополнительные грузи 7 и 8, которые используют для приведения системы в состояние движения. определения ускорения грузов запишем уравнение поступательного движения каждого груза (обозначение смотреть на рис. 2):
определения ускорения грузов запишем уравнение поступательного движения каждого груза (обозначение смотреть на рис. 2): . (1)
. (1)


