
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение момента инерции и проверка теоремы Штейнера методом крутильных колебанийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Цель работы: методом крутильных колебаний определить момент инерции тел, проверить теорему Штейнера. Теоретический материал.
 . Верхние концы нитей прикреплены к диску меньшего радиуса . Верхние концы нитей прикреплены к диску меньшего радиуса  . Трифілярний подвес крепится на специальном кронштейне, вмонтированному в стенку. . Трифілярний подвес крепится на специальном кронштейне, вмонтированному в стенку.
Платформа может делать крутильные колебания возле вертикальной оси, которая проходит через центры верхнего и нижнего дисков. Колебания возбуждаются поворотом верхнего диска с помощью шнура, связанного с ним и переброшенного через блок. При крутильных колебаниях платформы центр масс ее перемещается вдоль оси обращения. Если работа сил, которые приводят к потерям энергии имела в сравнимые с энергией запасенной в системе, то можно считать, что механическая энергия сохраняется, а колебание являются незатухающими (это первое предположение, на котором базируются дальнейшие расчеты). На рис.1 представленные две позиции платформы. Позиция а. Платформа проходит через положение равновесия. Механическая энергия есть чисто кинетической:
где: Позиция б. Платформа возвратила на угол j, при этом центр масс поднялся на высоту Полная механическая энергия системы определяется соотношением:
Обратимся теперь к методике определения момента инерции тела. Крайне редко экспериментатор имеет возможность провести прямые измерения необходимой величины. Обычно результат получают путем косвенных измерений. Таким образом, задачи сводится к установлению связи момента инерции с величинами, непосредственно измеренными на опыте. Очевидно, что в нашем случае это масса, время, геометрические характеристики системы: радиусы платформы - Установим связь между высотой
Используя теорему Пифагора находим (см. рис.1а):
Теорема косинусов разрешает найти
Подставляя выражение (3) и (4) в (2) после элементарных преобразований имеем:
Принимая во внимание неровности:
Таким образом, формула (5) принимает вид:
Для простоты расчетов будем считать колебание малыми, т.е.
Полная механическая энергия
Соответственно первому допущению
Возьмем во внимание известные кинематические соотношения:
после простых преобразований получаем:
Уравнение (9) є линейным, однородным дифференциальным уравнением второго порядка, решением которого является функция:
где:
Циклическая частота колебаний (связанная с периодом соотношением:
Учитывая (12) с (11) получаем:
Формула (13) устанавливает связь между моментом инерции платформы, периодом ее колебания, массой платформы и геометрических параметров системы. Поэтому формулу (13) следует рассматривать как рабочую. Порядок выполнения работы. 1. Возбудите малые колебания пустой платформы. Определите ее момент инерции 2. Положите на платформу тело, момент инерции которого нужно определить. Если тело имеет осевую симметрию, необходимо установить тело так, чтобы ось вращения проходила через его центр масс. Измерения
Проведите измерения (по предложению преподавателя) момента инерции тела, которое имеет осевую симметрию. Сопоставьте результаты измерений с расчетами. Следует учесть, что 3. Выше уже упоминалась о возможностях измерения момента инерции тела произвольной формы относительно любой оси, в том числе и относительно оси, которая проходит через центр масс. Поскольку положение последнего точно не известно, поступают таким образом. Проводят измерения периода колебания системы при разных положениях тела. В конечном итоге нужно найти такое положение, которому отвечает минимальный период. Определенный таким образом момент инерции будет отвечать моменту инерции относительно оси проходящей через центр масс (Чему?). Проверка теоремы Штейнера. Теорему Штейнера проверяют, пользуясь двумя одинаковыми телами. Для этого следует проделать следующий цикл измерений:
Сравните полученное значение с вычисленным соответственно теореме Штейнера:
где: В предотвращении перекосов тела следует располагать на платформе строго симметрично, для чего на платформе нанесенные концентрические окружности на определенном расстоянии друг от друга. Погрешности измерений. Вид формулы (13) разрешает сразу записать выражение для относительной погрешности момента инерции в виде:
Однако следует иметь в виду то, что момент инерции тела определяется как разность результатов измерений при нагруженной Учитывая то, что ошибки могут только накапливаться, можно оценить погрешность в определении
Как видно из (18) результат будет зависеть от соотношения между Принимая во внимание сказанное выше, самостоятельно проведите оценки погрешностей измерений Контрольные вопросы: 1. Какая величина называется моментом инерции тела? Какую роль играет момент инерции в динамике вращательного движения? 2. Сформулируйте и доведите теорему Штейнера. 3. В чем заключается метод трифилярного подвеса? Применение каких законов разрешает получить формулу для расчета момента инерции тел в данной работе? Получите формулу для расчета момента инерции. 4. Момент каких сил создает крутильные колебания системы? Учитывается ли в работе изменение силы натяжения нити в процессе колебаний? 5. Как изменяется период крутильных колебаний при изменении массы нижней платформы? Какое условие должна быть выполненная, чтобы колебания были гармоническими? 6. Каким образом, не изменяя массы груза на платформе, изменить период крутильных колебаний? Которое с найденных значений периодов отвечает такому положению тела на платформе, при котором ось вращения проходит через его центр масс? 7. Укажите возможные ошибки эксперимента. Литература: 1. Физический практикум под редакцией В.И. Ивероновой. Механика и молекулярная физика, -М., 1967. 2. А.Н.Матвеев. Механика и теория относительности, -М., 1976, §43, 50. 3. Д.В. Сивухин. Общий курс физики, т.I, -М., §35, 36, 42. 4. С.Э. Хайкин. Физические основы механики, -М., 1975, §59-6I, 64.
Лабораторная работа №10
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1692; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.009 с.) |

 Вращательное движение твердого тела. Момент силы, момент инерции. Теорема Штейнера. Момент импульса твердого тела относительно оси. Уравнение движения твердого тела. Уравнение моментов. Системы материальных точек и момент сил, которые действуют на систему материальных точек. Потенциальная и кинетическая энергии. Кинетическая энергия вращающегося твердого тела. Закон сохранения энергии. Консервативные и дисипативні системы. О законах сохранения и неконсервативные системы. Гармонические колебания. Амплитуда, период, частота.
Вращательное движение твердого тела. Момент силы, момент инерции. Теорема Штейнера. Момент импульса твердого тела относительно оси. Уравнение движения твердого тела. Уравнение моментов. Системы материальных точек и момент сил, которые действуют на систему материальных точек. Потенциальная и кинетическая энергии. Кинетическая энергия вращающегося твердого тела. Закон сохранения энергии. Консервативные и дисипативні системы. О законах сохранения и неконсервативные системы. Гармонические колебания. Амплитуда, период, частота.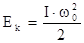 ,
, - момент инерции платформы (свободной или нагруженной),
- момент инерции платформы (свободной или нагруженной),  - угловая скорость в рассмотренный момент времени.
- угловая скорость в рассмотренный момент времени. , часть кинетической энергии перешла в потенциальную
, часть кинетической энергии перешла в потенциальную  , где
, где  - масса платформы (нагруженной и свободной).
- масса платформы (нагруженной и свободной). (1)
(1) и длины нитей -
и длины нитей -  .
. или
или  (2)
(2) (3)
(3) :
: (4)
(4) (5)
(5) имеем:
имеем: .
. (6)
(6) (второе предположение). Несложно убедиться, что при
(второе предположение). Несложно убедиться, что при  равенство
равенство  и
и  выполняется с погрешностью в
выполняется с погрешностью в  Поэтому при выполнении работы рекомендуют возбуждать колебание с амплитудой не превышающих нескольких угловых градусов. С учетом выше сказанного (6) принимает вид:
Поэтому при выполнении работы рекомендуют возбуждать колебание с амплитудой не превышающих нескольких угловых градусов. С учетом выше сказанного (6) принимает вид: (7)
(7) с учетом (1) определяется соотношением:
с учетом (1) определяется соотношением: (8)
(8) , итак, производная за временем выражение (8) равняется 0, т.е.:
, итак, производная за временем выражение (8) равняется 0, т.е.: .
.

 (9)
(9) (10)
(10) - амплитуда колебаний,
- амплитуда колебаний,  - начальная фаза, W - циклическая частота колебаний. Путем подстановки (10) в (9) легко убедиться, что функция (10) тождественно удовлетворяет уравнению (9) при условии равенства:
- начальная фаза, W - циклическая частота колебаний. Путем подстановки (10) в (9) легко убедиться, что функция (10) тождественно удовлетворяет уравнению (9) при условии равенства: (11)
(11) (12)
(12) (13)
(13) , используя формулу (13). С помощью секундомера проведите измерения времени 50-100 полных колебаний, который дает возможность довольно точно определить величину периода
, используя формулу (13). С помощью секундомера проведите измерения времени 50-100 полных колебаний, который дает возможность довольно точно определить величину периода  . Необходимые величины
. Необходимые величины  , а также масса платформы указанные в приложении к установке.
, а также масса платформы указанные в приложении к установке. :
: (14)
(14)
 Определите момент инерции одного тела
Определите момент инерции одного тела  от оси вращения соответственно чертам. 2б. Если
от оси вращения соответственно чертам. 2б. Если  (15)
(15) (16)
(16) - масса тела.
- масса тела. (17)
(17) .
. (18)
(18) погрешность при определении
погрешность при определении  ведь
ведь  . Таким образом, при измерении моментов инерции тел заметно меньших величины
. Таким образом, при измерении моментов инерции тел заметно меньших величины  ,
,  . Проанализируйте результаты экспериментов.
. Проанализируйте результаты экспериментов.


