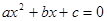Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Изучение колебаний струны и градуировка шкалы частот звукового генератораСодержание книги
Поиск на нашем сайте
Цель работы: исследовать условия образования стоячих волн в натянутой струне; на основании полученных данных проградуировать шкалу частот звукового генератора.
Теоретический материал. Динамика волнового процесса в упругой среде. Волновое уравнение. Энергия волны. Принцип Гюйгенса. Интерференция волн. Стоячие волны.
Рассмотрим колебание гибкой однородной струны с закрепленными концами.
Проекции сил натяжения Т струны на ось y, которые берутся в точках x и x + dx (рис.8), при малых углах α равняются
Разность этих проекций есть сила, которая действует на участок
Здесь r - погонная плотность, т.е. масса единицы длины струны. Поделим уравнение (1) на
Получим
Уравнение типа (3) называют волновыми уравнениями. В общем случае зависимость отклонения y от переменных x и t является сложной. В случае стоячей волны решение значительно упрощается. Стоячая волна имеет ту особенность, что все ее точки колеблются одновременно, хотя и с разными амплитудами. Таким образом, решение уравнения (3) можно изобразить в виде некоторой периодической функции времени B(t), амплитуда которой зависит от координаты x:
Чтобы найти функции
Как видим, левая часть уравнения (5) не зависит от t, а правая – от х. Так как переменные х и t являются независимыми, то это может иметь место только в том случае, если обе части уравнения (5) являются постоянными. Обозначим эту постоянную через -
и
Решением этих уравнений, как нетрудно убедиться непосредственной подстановкой, являются гармонические функции
Подставив полученные значения А и В в (4), найдем решение волнового уравнения
где Рассмотрим (8) более детально. Точки, в которых Объясним, почему перед Положительные значения
или
Как легко убедиться, Частота колебаний (может быть определена из (8)):
Если подставить найденное отсюда
Надо отметить, что определенная формулой (12) собственная частота не зависит от модуля Юнга материала струны. Такой, на первый взгляд, парадоксальный результат является следствием того, что мы не учли изменения натяжения струны при колебаниях. В условиях нашего опыта предположение, что С помощью (12) получим вместо (8)
Из этого соотношения видно, что точки струны с координатами Отметим, что волновому уравнению удовлетворяют не только решения в форме (8), но и сумма выражений типа (8) с разными
Таким образом, в струне могут одновременно существовать колебания с разными собственными частотами; рядом с основным тоном ( Выясним, при каких условиях приведенную выше теорию, которая описывает движение идеально гибкой струны в вакууме, можно применять для реальной струны. При колебании реальной струны всегда происходят потери энергии. Часть энергии теряется вследствие трения о воздух, другая часть проходит через концы струны и т.д. Для поддержки незатухающих колебаний используют вибратор. Если энергия потерь в точности компенсируется энергией, которая поступает от вибратору, то в струне можно наблюдать стоячие волны. Но теперь по струне должна происходить передача энергии. Поэтому рядом со стоячей будет существовать и бегущей волна, вследствие этого узлы будут немного размытыми. Если потери энергии за один период малы по сравнению с запасом колебательной энергии в струне, то искажение стоячей волны бегущей волной не очень существенны. Так как энергия волны пропорциональна квадрату амплитуды, то наши условия можно записать в виде:
где
При наблюдении стоячих волн в реальных условиях легко заметить, что струна не колеблется в одной плоскости, а вращается вокруг положение равновесия. Но любое вращательное движение можно представить как сумму колебаний в двух взаимно перпендикулярных плоскостях, так что предыдущие выводы остаются в силе. В работе исследуются колебания натянутой струны. Схема экспериментальной установки изображена на рис.9. У нижнего конца струны С имеется чашка весов, верхний конец прикреплен к язычку Я электромагнитного вибратору В, который служит для возбуждения колебаний. Обмотка вибратора питается синусоидальным током от звукового генератора ЗГ-33. Если нагрузить чашку весов и включить звуковой генератор, то от вибратора по струне побегут поперечные волны, которые отражаются от места ее закрепления. Образуется сложная картина колебаний. При медленном изменении частоты звукового генератора можно заметить, что при определенных частотах колебания струны стабилизируются - создаются стоячие волны. При этом струна делится неподвижными точками – узлами ‑ на несколько равных отрезков. Амплитуда колебаний отдельных точек струны перестает при этом зависеть от времени и определяется только их положением на струне. При изменении нагрузки на чашке весов картина колебаний сразу размывается. Если теперь изменить частоту звукового генератора, то можно снова получить стоячую волну с тем же числом узлов. Таким образом, частота колебаний стоячей волны зависит от натяжения струны.
Порядок выполнения работы. 1. Включить звуковой генератор. Установите частоту на нуль (смотри инструкцию к ЗГ-ЗЗ) и нагрузите струну. Вращайте ручку изменения частоты генератора и проведите наблюдение стоячих волн. Каждый раз записывайте количество пучностей 2. Повторите эксперимент при разных нагрузках (выполнить при пяти разных нагрузках). 3. Проверьте градуировку шкалы генератора. Для этого постройте график, на оси ординат которого отложите значение частоты колебаний струны, рассчитанные для разных 4. Постройте график зависимости частоты колебаний струны от величины натяжения.
Контрольные вопросы:
Литература:
Приложение
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 751; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.41.109 (0.007 с.) |

 Задача данной работы заключается в исследовании колебаний струны и градуировке звукового генератора по частоте. Для этого, прежде всего, необходимо получить формулу, которая бы связывала частоту колебаний струны с ее параметрами и натяжением.
Задача данной работы заключается в исследовании колебаний струны и градуировке звукового генератора по частоте. Для этого, прежде всего, необходимо получить формулу, которая бы связывала частоту колебаний струны с ее параметрами и натяжением.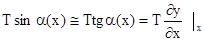 и.
и. 
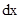 в направлении оси y. Можно записать второй закон Ньютона
в направлении оси y. Можно записать второй закон Ньютона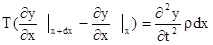 . (1)
. (1) . (2)
. (2)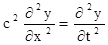 , (3)
, (3)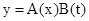 . (4)
. (4)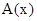 и
и 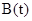 подставим (4) в волновое уравнение (3). Тогда получим
подставим (4) в волновое уравнение (3). Тогда получим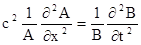 . (5)
. (5) (выбор знака перед
(выбор знака перед 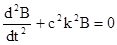 (6)
(6) , (7)
, (7)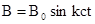 , и
, и 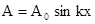 .
.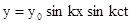 , (8)
, (8) - некоторая постоянная, которая определяет амплитуду колебаний и не имеет для нас существенного значения.
- некоторая постоянная, которая определяет амплитуду колебаний и не имеет для нас существенного значения. становится равным нулю, являются узлами стоячей волны. Между двумя соседними узлами все участки струны колеблются в одинаковой фазе (их скорости имеют одинаковые направления), а при переходе через узел фаза колебаний изменяется на
становится равным нулю, являются узлами стоячей волны. Между двумя соседними узлами все участки струны колеблются в одинаковой фазе (их скорости имеют одинаковые направления), а при переходе через узел фаза колебаний изменяется на 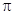 вследствие изменения знака
вследствие изменения знака  . Амплитуда колебаний изменяется вдоль струны по гармоническому закону, а частота колебаний всех точек струны постоянна и равняется
. Амплитуда колебаний изменяется вдоль струны по гармоническому закону, а частота колебаний всех точек струны постоянна и равняется 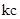 .
. был выбран знак минус. Если изменить этот знак, то решение уравнений (6) и (7) превратится в экспоненты с действительными показателями, которые описывают монотонное убывание, а не периодическое движение. Это не отвечает картине стоячей волны.
был выбран знак минус. Если изменить этот знак, то решение уравнений (6) и (7) превратится в экспоненты с действительными показателями, которые описывают монотонное убывание, а не периодическое движение. Это не отвечает картине стоячей волны. (
( - длина струны) дают
- длина струны) дают , (9)
, (9)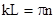 (
(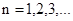 ). (10)
). (10)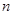 определяет количество пучностей (но не узлов) струны, которые колеблются. Таким образом, волновому уравнению с данными предельными условиями удовлетворяет не любая функция типа (8), а лишь те из них, для которых выполняется условие (10).
определяет количество пучностей (но не узлов) струны, которые колеблются. Таким образом, волновому уравнению с данными предельными условиями удовлетворяет не любая функция типа (8), а лишь те из них, для которых выполняется условие (10). . (11)
. (11)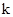 в (10) и использовать выражение (2), то получим формулу для собственных частот струны, т.е. частот, при которых в струне устанавливаются стоячие волны
в (10) и использовать выражение (2), то получим формулу для собственных частот струны, т.е. частот, при которых в струне устанавливаются стоячие волны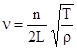 ; (T=mg) (12)
; (T=mg) (12)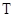 постоянно, хорошо выполняется.
постоянно, хорошо выполняется.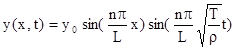 . (13)
. (13) являются узлами. Так как узлы все время остаются в покое, то энергия по струне не течет (энергия не может перейти через узлы). Передача энергии вдоль струны может происходить за счет бегущей волны.
являются узлами. Так как узлы все время остаются в покое, то энергия по струне не течет (энергия не может перейти через узлы). Передача энергии вдоль струны может происходить за счет бегущей волны. . (14)
. (14)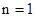 ) могут возбуждаться его гармоники (
) могут возбуждаться его гармоники ( ).
).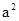 <<
<<  , (15)
, (15) - амплитуда волныбегущей, которую можно измерить по размыванию узла, а
- амплитуда волныбегущей, которую можно измерить по размыванию узла, а  - амплитуда стоячей волны, которая определяется в пучности, которая находится по соседству с данным узлом.
- амплитуда стоячей волны, которая определяется в пучности, которая находится по соседству с данным узлом.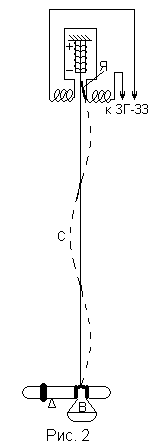 Следует отметить также, что приведенная выше теория выводилась для струны с жестко закрепленными концами, что в реальных условиях не выполняется. Но если перейти от рассмотрения всей струны к рассмотрению ее участка, который расположен между двумя узлами, то использование формул становится очевидным.
Следует отметить также, что приведенная выше теория выводилась для струны с жестко закрепленными концами, что в реальных условиях не выполняется. Но если перейти от рассмотрения всей струны к рассмотрению ее участка, который расположен между двумя узлами, то использование формул становится очевидным. при постоянном натяжении, а на оси абсцисс ‑ соответствующие деления, отмеченные на шкале генератора. Сделайте из графика вывод.
при постоянном натяжении, а на оси абсцисс ‑ соответствующие деления, отмеченные на шкале генератора. Сделайте из графика вывод.