Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
При помощи маятника ОбербекаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Цель работы: экспериментальным путем определить момент инерции системы; сравнить полученный результат с теоретическим значением с целью проверки основного уравнения динамики вращательного движения твердого тела.
Теоретический материал. Вращательное движение твердого тела. Момент силы, момент инерции. Теорема Штейнера. Уравнение движения тела. Второй закон Ньютона. Угловая скорость и. ускорение. Векторы угловой скорости и ускорение. Нормальное и тангенциальное ускорение. Связь тангенциального ускорения с угловым.
В работе изучается динамика вращательного движения. В частности, экспериментально проверяется уравнение моментов для вращения вокруг неподвижной оси
где
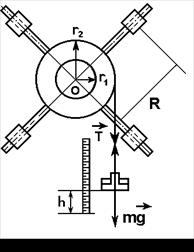
 каждый. Втулка и два шкива радиусами каждый. Втулка и два шкива радиусами  и и  насажены на общую ось. Ось закреплена в подшипниках, так что вся система может вращаться вокруг горизонтальной оси. Передвигая грузы по спицам, можно легко изменять момент инерции насажены на общую ось. Ось закреплена в подшипниках, так что вся система может вращаться вокруг горизонтальной оси. Передвигая грузы по спицам, можно легко изменять момент инерции  тела. На шкив намотана нить, к которой привязана платформа известной массы. На платформу ложится груз, нить натягивается и создает вращающий момент тела. На шкив намотана нить, к которой привязана платформа известной массы. На платформу ложится груз, нить натягивается и создает вращающий момент
где
где
Из уравнений (2) и (3) получаем, что момент силы натяжения нити
Кроме того, на маятник действует момент силы трения в оси
В уравнение (6) входит ускорение Действительно, измеряя время
Тогда
Формула (8) дает связь между ускорением Момент инерции, который входит в (8), в соответствии с теоремой Гюйгенса-Штейнера, может быть записан в виде
Здесь В (8) входит также отношение
В условиях опыта оно меньше или порядка
Измерение. Представляет интерес экспериментально исследовать две зависимости. Первая ‑ зависимость углового ускорения Если на оси ординат откладывать угловое ускорение Если экспериментальные данные подтверждают линейную зависимость Соответственно теореме Гюйгенса-Штейнера.
Выясним, как проверить эту зависимость экспериментально. Для этого превратим соотношение (10), пренебрегая в нем малой величиной (моментом силы трения
Итак,
Из (11) понятно, как экспериментально проверить зависимость (11): нужно, выбрав постоянную массу Если экспериментальные точки в пределах точности измерений ложатся на прямую, то это подтверждает зависимость (11), а значит, и формулу
Отметим, что при выведеннии формулы (11) мы презрели моментом сил трения, т.е. считали, что Роль момента сил трения можно оценить и иначе. Для этого заметим, что если маятник в начальный момент вращается с угловой скоростью
где
где С (12) и (13) находим
Пусть
Отсюда видно, как на опыте определить Задача 1. Сбалансируйте маятник. Для этого оставьте на крестовине два груза на двух противоположных спицах на равных расстояниях от оси вращения. Спицы, на которых находятся грузы, соединенные со втулкой резьбой. Оборачивая спицы в резьбе, добейтесь равновесия. Потом точно сбалансируйте грузы на второй паре спиц на таком же расстоянии от оси вращения. Полезно несколько раз привести маятник во вращение, каждый раз давая ему возможность остановиться. Подумайте, как на основании этих опытов определить, хорошо ли сбалансирован маятник. 2. Определите приблизительно минимальную массу
где 3. Оцените ускорение 4. Определите экспериментально зависимость углового ускорения Для определения зависимости
и определить среднее ускорение груза с соотношение (7):
Эти измерения и вычисления повторите для пяти значений массы Результаты измерений запишите в табл. 1. Таблица 1.
1. Величина
2. Угловое ускорение находится за формулой 3. Полученные экспериментально точки отложите в координатной плоскости 5. Проверьте экспериментально зависимость (11). Для этого, взяв постоянную массу груза

В каждом положении Полученные экспериментальные точки нанесите с учетом погрешностей в координатной плоскости
Таблица 2
Контрольные вопросы: 1. Выведите основное уравнение динамики вращательного движения твердого тела вокруг недвижимой оси. Между какими величинами устанавливается связь в этом уравнении? 2. Что называют моментом силы? Как направленный момент силы? Чему равняется его величина? Что такое плечо силы? Моменты каких сил действуют на систему в данной работе? Как в работе определяется момент силы трения? 3. Что такое момент инерции? Каково его физическое содержание? Запишите основное уравнение динамики вращательного движения относительно системы, рассмотренной в работе. 4. Как определить силу натяжения нити, на которой подвешен груз? Изменится ли сила натяжения, если маятник вместе с грузом затормозить? 5. При каком условии по ускорению груза, подвешенного на нити, можно определить угловое ускорение системы? 6. Сформулируйте и докажите теорему Штейнера. Применяя теорему Штейнера, выведите расчетную формулу для момента инерции системы. 7. Укажите возможные ошибки эксперимента.
Литература: 1. Руководство к лабораторным занятиям по физике под редакцией Л.Л. Гольдина, -М.: Наука, 1973. 2. Д.В. Сивухин. Общий курс физики. Механика, т.I, -M., Наука. 1974. гл. II. §11. гл. V §30, 32, 33.35. 3. И.В. Савельев. Курс общей физики, т. I, Механика, колебания и волны, молекулярная физика. Наука, 1973. §18, 19, 36, 37. 4. С.П. Стрелков. Механика, Наука. 1965, §52, 59. 5. С.Э. Хайкин, Физические основы механики, "Наука", 1971. §49-52, 67, 68.
Лабораторная работа № 7
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 2294; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.012 с.) |

 , (1)
, (1) ‑ угловое ускорение;
‑ угловое ускорение;  ‑ сумма проекций на ось вращения моментов внешних сил.
‑ сумма проекций на ось вращения моментов внешних сил. (2)
(2)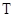 ‑ сила натяжения нити,
‑ сила натяжения нити, 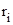 ‑ радиус шкива (
‑ радиус шкива ( (3)
(3) ‑ масса платформы с грузом,
‑ масса платформы с грузом, 
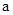 ‑ ее ускорение. Ускорение
‑ ее ускорение. Ускорение 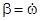 в случае отсутствия проскальзывания нити соотношением
в случае отсутствия проскальзывания нити соотношением (4)
(4)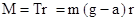 (5)
(5) . С учетом этого уравнение (1) имеет вид
. С учетом этого уравнение (1) имеет вид (6)
(6) , на протяжении которого платформа с грузом опускается на расстояние
, на протяжении которого платформа с грузом опускается на расстояние  , можно найти ускорение
, можно найти ускорение  (7)
(7)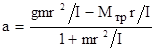 (8)
(8) . Хотя интуитивно понятно, что момент силы трения мал, тем не менее он не настолько мал, чтобы им в (8) можно было полностью пренебречь. Если положить
. Хотя интуитивно понятно, что момент силы трения мал, тем не менее он не настолько мал, чтобы им в (8) можно было полностью пренебречь. Если положить  , то можно убедиться, что результаты опыта будут отличаться от зависимости (8). Можно по порядку величины экспериментально определить
, то можно убедиться, что результаты опыта будут отличаться от зависимости (8). Можно по порядку величины экспериментально определить  , при которой маятник начнет вращаться. Дальнейшие измерения нужно проводить с грузами массой
, при которой маятник начнет вращаться. Дальнейшие измерения нужно проводить с грузами массой  . На первый взгляд относительную роль момента силы трения можно уменьшить, если взять грузы массой
. На первый взгляд относительную роль момента силы трения можно уменьшить, если взять грузы массой 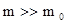 , допустим, груз
, допустим, груз  . Однако это не так по двум причинам. Первая ‑ увеличение массы груза приводит к увеличению силы давления
. Однако это не так по двум причинам. Первая ‑ увеличение массы груза приводит к увеличению силы давления  на ось, а значит и к росту момента силы трения
на ось, а значит и к росту момента силы трения 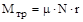 , где
, где  - коэффициент трения,
- коэффициент трения, 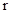 - плечо силы трения. Вторая причина заключается в том, что увеличение
- плечо силы трения. Вторая причина заключается в том, что увеличение  . (9)
. (9) ‑ расстояние центров грузов
‑ расстояние центров грузов  от оси вращения,
от оси вращения, 
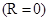 , т.е. равняется моменту инерции системы при
, т.е. равняется моменту инерции системы при  .
.
 (убедитесь в этом!). Пренебрегая этой величиной в выражении (8), получаем формулу, которую можно проверить экспериментально:
(убедитесь в этом!). Пренебрегая этой величиной в выражении (8), получаем формулу, которую можно проверить экспериментально: (10)
(10) от момента внешней силы
от момента внешней силы  при условии, что момент инерции
при условии, что момент инерции  , то. согласно (10), экспериментальные точки должны размещаться на прямой. Из (10) видно, что наклон этой прямой равняется
, то. согласно (10), экспериментальные точки должны размещаться на прямой. Из (10) видно, что наклон этой прямой равняется  , а точка сечения с осью абсцисс дает
, а точка сечения с осью абсцисс дает  , то можно приступить к изучению второй зависимости - зависимости момента инерции
, то можно приступить к изучению второй зависимости - зависимости момента инерции  .
.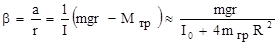 .
. . (11)
. (11) на спицах. Результаты измерений удобно изобразить в виде точек на координатной плоскости
на спицах. Результаты измерений удобно изобразить в виде точек на координатной плоскости  , где
, где  ,
,  .
.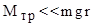 . Значение
. Значение  получено из графика зависимости
получено из графика зависимости  при
при  . Это и разрешает выбрать массу перегрузки так, чтобы неравенство
. Это и разрешает выбрать массу перегрузки так, чтобы неравенство  сознательно выполнялась.
сознательно выполнялась. , то к моменту остановки он повернется на угол
, то к моменту остановки он повернется на угол  , который можно определить из соотношения
, который можно определить из соотношения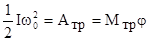 , (12)
, (12)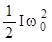 - начальная кинетическая энергия вращающегося маятника,
- начальная кинетическая энергия вращающегося маятника,  - работа сил трения. В (12) предполагается, что момент сил трения является постоянной величиной и связан с угловым ускорением соотношением
- работа сил трения. В (12) предполагается, что момент сил трения является постоянной величиной и связан с угловым ускорением соотношением , (13)
, (13) - ускорения, которые определяются только моментом сил трения.
- ускорения, которые определяются только моментом сил трения. . (14)
. (14) - полное число оборотов, которое делает маятник до остановки, а
- полное число оборотов, которое делает маятник до остановки, а  - период вращения маятника в начале движения. Тогда
- период вращения маятника в начале движения. Тогда 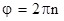 ,
,  и с (14) получаем
и с (14) получаем (15)
(15) .
. , при которой маятник начинает вращаться, и оцените момент сил трения из соотношение
, при которой маятник начинает вращаться, и оцените момент сил трения из соотношение ,
, .
. измерьте время
измерьте время 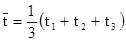



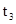

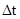
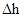

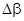



 .
. определяется точностью, с которой вымеренная масса грузов
определяется точностью, с которой вымеренная масса грузов 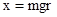 ,
,  и по ним постройте график зависимости
и по ним постройте график зависимости  (рис. 2а).
(рис. 2а). ,
,  и постройте график зависимости
и постройте график зависимости  (рис. 2, б).
(рис. 2, б).