
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение скорости распространения звука методом интерференции волнСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цель работы: определить скорость звука в воздухе методом интерференции звуковых волн. Оценить погрешность эксперимента. Теоретический материал. Продольные и поперечные волны. Уравнение плоской волны. Амплитуда, фаза и частота волны. Динамика волнового процесса в упругой среде. Энергия волны. Поток энергии. Принцип Гюйгенса. Интерференция волн. В физике волнами или волной называют всякое чередование со временем в пространстве максимумов и минимумов любой физической величины, например, плотности вещества, напряженности электрического поля, температуры. Волной часто называют также явления, при которых в пространстве происходит распространение кратковременного электрического или механического “толчка”. Волновой процесс будет задан, если в любые моменты времени известны смещения колеблющихся частиц, расположенных на разных расстояниях от источника волн. Итак, волновой процесс будет определен, если известна функциональная зависимость смещения колеблющейся частицы от координат ее точки равновесия x, y, z и времени t, т.е.
Найдем вид функции (1). Для упрощения рассмотрим плоскую волну, которая распространяется в направлении оси Оx. В этом случае волновые поверхности (геометрические места точек, которые колеблются в одинаковых фазах) будут перпендикулярны оси OX, а смещение колеблющихся точек этих поверхностей зависят только от x и t, т.е. Рассмотрим частный случай. Пусть смещение частицы, лежащей в плоскости x=0, определяется уравнением
Смещение частиц в плоскости, которая расположена на расстоянии x от начальной, происходит позднее на время t. За это время волна распространяется от плоскости x=0 до заданной. Ведь
Поскольку
Так как длина волны
В среде могут распространяться несколько волн. Опыт показывает, что каждая волна распространяются независимо от наличия других волн. Частица среды при этом осуществляет колебания, которые являются результатом сложения колебаний, которые создаются в данной точке пространства каждой волной. Результирующее смещение частицы среды в любой момент времени равняется геометрической сумме смещений, которые осуществляет частица под действием каждой волны в отдельности. Только при определенных условиях при наложении двух волн амплитуды результирующих колебаний разных частиц среды будут иметь неодинаковые величины, значение которых со временем не будет изменяться. В одних местах наблюдается усиление колебаний, в других - ослабление. В общем случае амплитуда результирующих колебаний не равняется сумме амплитуд составляющих колебаний. Это явление наложения волн называют интерференцией. Характерным признаком интерференции является существование зон с максимальными и минимальными амплитудами результирующих колебаний. Эти зоны чередуются, но не перемещаются. Интерференционная картина возникает, когда колебание частиц среды, которые возбуждаются интерферирующимися волнами, происходят в одинаковых направлениях, частоты их колебаний одинаковы и сдвиг фаз между колебаниями частички со временем не изменяется. Волны, которые удовлетворяют этим условиям, называют когерентными. Такое название отвечает и источнику их возбуждения. Пусть в какую-то точку, которая расположена на расстояниях
При добавлении колебаний одного направления найдем амплитуду результирующего колебания
где Из выражения (6) следует, что амплитуда результирующего смещения будет максимальной и равной
Из (6) также следует, что амплитуда результирующих колебаний имеет минимальное значение
т.е. для значений разности хода волн равных нечетному числу длин полуволн:
Таким образом, в случае сложения когерентных волн, результирующее колебание в каждой точке среды имеет постоянную по времени амплитуду, которая зависит от расстояния этой точки до источников колебаний.
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 723; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.155.48 (0.006 с.) |

 , (1)
, (1)
 .
. , (2)
, (2) , (3)
, (3)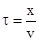 , где v – скорость распространения волн, то (3) перепишем так
, где v – скорость распространения волн, то (3) перепишем так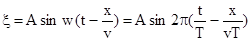 .
.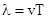 , а волновое число
, а волновое число 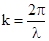 , то
, то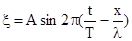 , или
, или 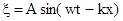 , (4)
, (4) и
и 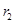 от когерентных источников, в момент времени t доходят две когерентные волны
от когерентных источников, в момент времени t доходят две когерентные волны ,
, , (5)
, (5)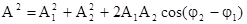 , (6)
, (6)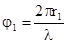 ,
, 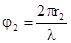 . Тогда
. Тогда 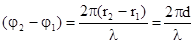 .
. в тех точках, для которых разность хода волн
в тех точках, для которых разность хода волн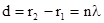 ,
, 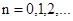 , (7)
, (7)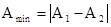 для разностей фаз, когда
для разностей фаз, когда ,
, 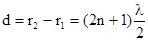 , (8)
, (8)


