
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерференция волн. Принцип Гюйгенса-ФренеляСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ИНТЕРФЕРЕНЦИЯ ВОЛН - такое наложение волн, при котором происходит устойчивое во времени их взаимное усиление в одних точках пространства и ослабление в других, в зависимости от соотношения между фазами этих волн. Необходимые условия для наблюдения интерференции: 1) волны должны иметь одинаковые (или близкие) частоты, чтобы картина, получающаяся в результате наложения волн, не менялась во времени (или менялась не очень быстро, что бы её можно было успеть зарегистрировать); 2) волны должны быть однонаправленными (или иметь близкое направление); две перпендикулярные волны никогда не дадут интерференции (попробуйте сложить две перпендикулярные синусоиды!). Иными словами, складываемые волны должны иметь одинаковые волновые векторы (или близконаправленные). Волны, для которых выполняются эти два условия, называются КОГЕРЕНТНЫМИ. Первое условие иногда называют временной когерентностью, второе - пространственной когерентностью. Рассмотрим в качестве примера результат сложения двух одинаковых однонаправленных синусоид. Варьировать будем только их относительный сдвиг. Иными словами, мы складываем две когерентные волны, которые отличаются только начальными фазами (либо их источники сдвинуты друг относительно друга, либо то и другое вместе). Если синусоиды расположены так, что их максимумы (и минимумы) совпадают в пространстве, произойдет их взаимное усиление. Если же синусоиды сдвинуты друг относительно друга на полпериода, максимумы одной придутся на минимумы другой; синусоиды уничтожат друг друга, то есть произойдет их взаимное ослабление. Математически это выглядит так. Складываем две волны:
здесь х1 и х2 - расстояния от источников волн до точки пространства, в которой мы наблюдаем результат наложения. Квадрат амплитуды результирующей волны (пропорциональный интенсивности волны) дается выражением:
Максимум этого выражения есть 4A2, минимум - 0; всё зависит от разности начальных фаз и от так называемой разности хода волн Δ:
При в данной точке пространства будет наблюдаться интерференционный максимум, при В нашем простом примере источники волн и точка пространства, где мы наблюдаем интерференцию, находятся на одной прямой; вдоль этой прямой интерференционная картина для всех точек одинакова. Если же мы сдвинем точку наблюдения в сторону от прямой, соединяющей источники, мы попадем в область пространства, где интерференционная картина меняется от точки к точке. В этом случае мы будем наблюдать интерференцию волн с равными частотами и близкими волновыми векторами. Принцип Гюйгенса-Френеля. Дифракцией называется совокупность явлений, наблюдаемых при распространении света в среде с резкими неоднородностями и связанных с отклонениями от законов геометрической оптики. Для наблюдения дифракции световых волн необходимо, чтобы препятствия были соизмеримы с длиной световой волны. Согласно принципу Гюйгенса каждая точка пространства, до которой доходит волна, служит центром вторичных волн, огибающая которых задает положение волнового фронта в следующий момент времени. Волновой фронт − геометрическое место точек, до которых доходят колебания к моменту времени t. Принцип Гюйгенса решает лишь задачу о направлении распространения волнового фронта, но не затрагивает вопроса об амплитуде, (интенсивности) волн, распространяющихся по разным направлениям. Френель вложил в принцип Гюйгенса физический смысл, дополнив его идеей интерференции вторичных волн. Согласно принципу Гюйгенса-Френеля световая волна, возбуждаемая каким-либо источником S может быть представлена как результат суперпозиции когерентных вторичных волн. Каждый элемент волновой поверхности S (рис.) служит источником вторичной сферической волны, амплитуда которой пропорциональна величине элемента dS.
Амплитуда этой вторичной волны убывает с расстоянием r от источника вторичной волны до точки наблюдения по закону 1/r. Следовательно, от каждого участка dS волновой поверхности в точку наблюдения Р приходит элементарное колебание:
Результирующее колебание в точке Р представляет собой суперпозицию колебаний (1), взятых для всей поверхности S:
Эта формула является аналитическим выражением принципа Гюйгенса-Френеля.
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 634; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.250.115 (0.007 с.) |




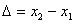
 - интерференционный минимум.
- интерференционный минимум.
 где (ωt + α0) − фаза колебания в месте расположения волновой поверхности S, k − волновое число, r − расстояние от элемента поверхности dS до точки P, в которую приходит колебание. Множитель а0 определяется амплитудой светового колебания в месте наложения элемента dS. Коэффициент K зависит от угла φ между нормалью к площадке dS и направлением на точку Р. При φ = 0 этот коэффициент максимален, а при φ/2 он равен нулю.
где (ωt + α0) − фаза колебания в месте расположения волновой поверхности S, k − волновое число, r − расстояние от элемента поверхности dS до точки P, в которую приходит колебание. Множитель а0 определяется амплитудой светового колебания в месте наложения элемента dS. Коэффициент K зависит от угла φ между нормалью к площадке dS и направлением на точку Р. При φ = 0 этот коэффициент максимален, а при φ/2 он равен нулю.



