Принцип гюйгенса - френеля. Зоны френеля. Дифракция френеля на круглом экране и круглом отверстии

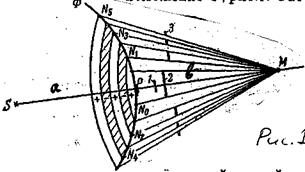
Дифракцией называется совокупность явлений, наблюдаемых при распространении света в среде с резкими неоднородностями и связанных с отклонениями от законов геометрической оптики. Дифракция, в частности, приводит к огибанию световыми волнами препятствий и проникновению света в область геометрической тени. Огибание препятствий звуковыми волнами (т.е. дифракция звуковых волн) наблюдается постоянно в обыденной жизни. Например, звук хорошо слышен за углом дома, т.е. звуковая волна его огибает. Для наблюдения дифракции световых волн необходимо создание спец. условий. Это обусловлено малостью длин световых волн. В пределе при l®0 законы волновой оптики переходят законы геометрической оптики. Следовательно, отклонения от законов геометрической оптики при прочих равных условиях оказываются тем меньше, чем меньше длина волны. Между интерференцией и дифракцией нет существ, различия. Оба явления заключаются в перераспределении светового потока в результате суперпозиции волн. По историческим причинам перераспределение интенсивности, возникающее в результате суперпозиции волн, возбуждаемых конечным числом дискретных когерентных источников, принято называть интерференцией волн, а вследствие суперпозиции волн, возбуждаемых когерентными источниками, расположенными непрерывно, принято называть дифракцией.

Наблюдение дифракции осуществляется обычно по следующей схеме. На пути св. волны, распространяющейся от некоторого источника, помещается непрозрачная преграда, закрывающая часть волновой поверхности св. волны. За преградой располагается экран, на котором возникает дифракционная картина.

Различают два вида дифракции. Если источник света S и точка наблюдения М расположены от препятствия настолько далеко, что лучи, падающие на препятствие, и лучи, идущие в точку М образуют практически параллельные пучки, говорят о дифракции в параллельных лучах или о дифракции Фраунгофера. В противном случае говорят о дифракции Френеля.

Проникновение световых волн в область геометрической тени можно объяснить с помощью принципа Гюйгенса, согласно которому каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн задает положение волнового фронта в следующий момент времени. Однако этот принцип не дает сведений об амплитуде (интенсивности) волн, распространяющихся в различных направлениях. Френель дополнил пр. Гюйгенса представлением об интерференции вторичных волн. Учет амплитуд и фаз вторичных волн позволяет найти амплитуду результирующей волны в любой точке пространства. Развитый т.о. принцип Гюйгенса получил название принципа Гюйгенса - Френеля: все источники вторичных волн, расположенные на поверхности фронта волны, когерентны между собой; световая волна в любой точке пространства является результатом интерференции волн, излучаемых вторичными источниками и достигших этой точки. Френель исключил возможность возникновения обратных вторичных волн. Поскольку точек фронта, являющихся когерентными источниками новых волн, бесчисленное множество, то расчет интерференции, в принципе, сводится к довольно громоздкому интегрированию. Для упрощения решения этого вопроса Френелем был предложен метод разделения фронта волны на зоны, так что волны от соседних зон приходят в точку наблюдения в противоположной фазе и ослабляют друг друга. С этим методом зон Френеля ознакомимся при анализе важнейшего вопроса: как волновая теория объясняет практическую прямолинейность распространения света и каковы границы применимости законов геометрической оптики, основанных на этой прямолинейности.

Пусть S - точечный источник монохроматического света в однородной среде. По принципу Гюйгенса от него распространяется во все стороны сферическая волна. В некоторый момент времени фронт этой волны занимает положение Ф, рис.1. Рассмотрим произвольную точку М перед фронтом и соединим её прямой линией с источником S.

Если бы свет распространялся прямолинейно вдоль луча SРМ, то достаточно было бы поставить на его пути сколь угодно малый экран 1, чтобы в точке М была полная темнота. Благодаря волновой природе света в точку наблюдения М приходят волны не только от точки Р, но и от всех остальных точек фронта Ф, правда в различных фазах.

Для расчета результатов интерференции Френель предложил провести ряд сфер с центрами в точке М и радиусами, соответственно равными

МN₁ = МP +l/2,

MN₂ = МN₁ +l/2 = МP + 2l/2,

MN₃ = МN₂ +l/2 = МP + 3l/2, и т.д. (1)

 

Тем самым фронт волны Ф разобьется на ряд кольцевых зон, заштрихованных на рис.1 через одну. Волны, приходящие в М от точек каждой последующей зоны, сдвинуты по отношению к волнам, приходящим от соответствующих точек предыдущей зоны, на Я./2, т.е. находятся в противоположных фазах, и их амплитуды при интерференции вычитаются. Из геометрического рассмотрения можно получить выражение для радиуса внешней границы т - ной зоны

Занумеруем величины суммарных амплитуд волн, приходящих в точку М от каждой последующей зоны:

А₀, А₁, А₂, а₃, А₄, А₅, А₆,....

Благодаря различию в расстояниях зон до точки наблюдения и в углах, под которыми видны эти площадки из М, величины этих амплитуд монотонно убывают:

А₀ > А₁> А₂> а₃> А₄> А₅> А₆,....

В качестве допустимого приближения можно принять, что амплитуда колебания от некоторой k - той зоны Френеля А_k равна среднему арифметическому от амплитуд примыкающих к ней зон:

 

А_k = (А_k+1 + А_k-1)/2. (2)

Полная амлитуда волны, приходящей в точку М, равна сумме амплитуд, создаваемых каждой отдельной зоной. При этом амплитуды от всех четных зон надо считать с одинаковым знаком (например, положительными), а амплитуда волн от всех нечетных зон (приходящих в) - с обратным знаком. Т.о.,

А = А₀-А₁ + А₂ –А₃,+ А₄- А₅ +.... (3)

Используя (2), можно это выражение представить в виде

 

А = А₀/2 + (А₀/2 – А₁ +А₂/2) + (А₂/2 -Аз + А₄ /2) +...» А₀/2, (4)

 

так как оставшаяся часть от амплитуды последней зоны ±А _k /2 практически ничтожно мала.

Т.о., суммарная амплитуда от воздействия всего фронта Ф в точке наблюдения М равна А = А₀/2, т.е. эквивалентна половине воздействия нулевойзоны Френеля.

Не следует при этом думать, что в М приходит свет только от всех точек половины нулевой зоны Френеля, остальные же участки фронта Ф, интерферируя, гасят др. др. Если на пути света от точечного источника поставить не слишком большой круглый экран 2 так, чтобы перпендикуляр, опущенный на него из источника света, проходил через его центр, то в М по-прежнему будет свет, хотя и меньшей интенсивности.

Действительно, проведя через край экрана 2 линию МN₀, мы можем произвести деление фронта, начиная от точки N₀, на такие же зоны Френеля, как и ранее. Повторяя все рассуждения, легко убедиться, что для идеального круглого экрана 2 суммарная амплитуда в М будет А' = А₀¢/2, где а₀' - амплитуда от нулевой зоны, отсчитываемой от N₀. По мере увеличения экрана 2 величина А' будет убывать, но точка М остается освещенной всегда практически до тех пор, пока экран не закроет достаточно большого числа зон Френеля. Лишь в этом последнем случае станет справедливым положение геометрической оптики, что препятствие, перекрывающее луч SМ, даст в точке наблюдения отсутствие света (геометрическая тень).

Более того, если например, сделать "зонный экран" 3, состоящий из ряда колец, закрывающих все нечетные (или все четные) зоны Френеля, то суммарная амплитуда

А= А₀ +А₂ + А₄ +.... (5)

оказывается даже большей, чем при отсутствии всякого экрана. Т.е такой экран действует подобно собирательной линзе. Еще большего эффекта можно достичь, не перекрывая четные (или нечетные) зоны, а изменяя фазу их колебаний на p. Это можно осуществить с помощью прозрачной пластинки, толщина которой в местах, сотв. четным или нечетным зонам, отличается на надлежащим образом подобранную величину. Такая пластинка называется фазовой зонной пластинкой. По сравнению с перекрывающей зоны амплитудной зонной пластинкой фазовая даст дополнительное увеличение амплитуда в два раза, а интенсивности света - в 4 раза.

Деление фронта волны Ф на зоны Френеля является относительным и зависит от расстояния до точки наблюдения М,

Пренебрегать дифракционными явлениями и рассматривать свет распространяющимся прямолинейно вдоль лучей, исходящих от источника, допустимо лишь, если размеры экрана велики по ср. с размерами зон Френеля. Чем короче l, тем меньше размеры этих зон и тем точнее можно пользоваться приближенными понятиями лучевой (геометрической) оптики. Т.к. для видимого света l = 0,4 - 0,8 мкм, то при наблюдении макроскопических тел этими приближениями можно пользоваться с достаточной точностью. Однако при уменьшении размеров тел начинают проявляться дифракционные явления.

Поставим на пути сферической световой волны непрозрачный экран с вырезанным в нем круглым отверстием радиуса г. Расположим экран так, чтобы перпендикуляр, опущенный из источника света S, попадал в центр отверстия. На продолжении этого перпендикуляра возьмем точку Р. Если расстояния а и b удовлетворяют соотношению (*), где m - целое число, то отверстие оставит открытым ровно m первых зон Френеля, построенных для точки Р. Из (*) число открытых зон Френеля определяется выражением

m = r₀²(1/а+1/b)/l. (6)

В соответствии с (3) амплитуда в точке Р будет равна

А = А₁ -А₂ +А₃ –А₄ +....±А_m (7)

Перед А_m берется знак «+», если m нечетное, и минус, если m - четное. Представив (7) в виде, аналогичном (4), и положив выражения в скобках равными нулю, получим

А = А₁/2 + А_m /2 (m - нечетное),

А=А₁/2 +А_m-1/2 – А_m (m - четное).

Амплитуды от двух соседних зон практически одинаковы. Поэтому (А_m-1/2) – А_m можно заменить через - А_m/2. В результате получится:

А = А₁/2 ± А_m/2,

где знак «+» берется для нечетных m и минус - для четных.

Для малых m амплитуда А_m мало отличается от А₁. Следовательно, при нечетных m амплитуда в точке Р будет приблизительно равна а₁, при четных m - нулю.

А какая будет освещенность в других точках экрана? Вследствие симметричного расположения отверстия относительно прямой SР освещенность в разных точках экрана будет зависеть только от расстояния х от точки Р. Если смещаться по экрану в точку Р¢ и далее, то дифракционная картина будет иметь вид чередующихся светлых и темных концентрических колец. Если отверстие открывает лишь часть центральной зоны Френеля, на экране получается размытое светлое пятно; чередования светлых и темных колец в этом случае не возникает.

Аналогичная картина на экране получается и в рассмотренном выше случае, когда между источником света и экраном помещается непрозрачный круглый диск. Дифракционная картина на экране будет иметь вид чередующихся светлых и темных концентрических колец. В центре картины помещается светлое пятно.