
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементарный импульс силы, действовавший на материальную точку в течение промежутка времени Dt , равен изменению ее количества движения за тот же промежуток времени.Содержание книги
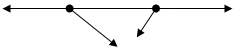
Поиск на нашем сайте В случае переменной силы, действующей в течение достаточно большого промежутка времени, последний следует разбить на достаточно малые элементарные интервалы Dtk так, чтобы на каждом интервале можно было заменить силу ее средним значением в этом интервале `Fk. Пронумеровав все последовательные положения движущейся точки на ее траектории как на рис., применим (4) последовательно к каждому интервалу. Для 1-го интервала Dt1 = t1 – t0 получим: `F1Dt1 =m` V 1 -m` V0, Аналогично далее: `F2 Dt2 = m` V 2 - m` V 1 __- - - - - - - - - - - - - - - - `Fk Dtk = m` V k - m` V k-1 - - - - - - - - - - - - - - - - - `FnDtn = m` V n – m` V n-1. Сложим все эти равенства. Тогда промежуточные значения вектора количества движения попарно сократятся, и мы получим: `F1 Dt1 +`F2 Dt2 + ….+`Fk Dtk + ….+ `Fn Dtn =m` V n- m` V 0(5) å`Fk Dtk – наз. полным импульсом переменной силы за время tn – t0. å`Fk Dtk = m` V n- m` V 0, (6) т.е. полный импульс переменной силы равен полному изменению количества движения за все время действия силы. Закон изменения количества движения (6) позволяет по начальной скорости ` V 0 и известному полному импульсу силы находить сразу конечную скорость` V n без вычисления всех промежуточных скоростей. Вычисление полного импульса å`Fk Dtk в общем случае произвольных сил также представляет собой довольно сложную задачу, решаемую методами интегрального исчисления. Закон изменения количества движения является непосредственным следствием 2-го закю Ньютона. Используя наряду с ним и 3-ий закон Ньютона, получим так называемый закон сохранения количества движения. Для этого рассмотрим две взаимодействующие материальные точки массами m1 и m2. Обозначим скорости движения этих точек в данный момент времени соотв. ` V1 и ` V 2(рис. 2.) `F21 m1 m2 `F12
`V2 `V1 Рис.2. Если первая из этих точек действует на вторую с `F12, то 2-я по 3-му закону Ньютона, действует на 1-ю с силой `F21 = -`F12. Под действием этих сил за промежуток времени Dt скорости точек получают приращения D` V 1 и D` V 2 и их количества движения изменяются соответственно на величину D(m1 V 1) и D(m2 V 2). Применяя закон изменения количества движения (4) к движению каждой точки в отдельности, можно написать: `F21Dt = D(m1 ` V 1), `F12Dt = D(m2 ` V 2) (7)
Складывая эти два равенства и учитывая, что `F12 = -`F21, получаем:
0 = D(m1 ` V 1) + D(m2 ` V 2) =D(m1 ` V 1 + m2 ` V 2). (8) Рассматриваемые две материальные точки, взаимодействующие только друг с другом, образуют систему, изолированную от действия всех остальных тел. Геометрическая сумма количества движения обеих точек m1 V 1 +m2 V 2 наз. количеством движения системы. Из (7) и (8) следует, что за время движения количество движения каждой точки в отдельности может изменяться, но количество движения системы остается постоянным: m1` V1 + m2` V 2 = const (9) Аналогичным способом может быть выведен закон сохранения количества движения для системы, состоящей из любого числа материальных точек или тел, взаимодействующих только между собой. В изолированной системе материальных тел количество движения всей системы в целом остается неизменным: åmi` V i = const. При механическом движении увеличение количества движения одного тела равно уменьшению количества движения всех остальных взаимодействующих с ним тел. Взаимодействующие тела обмениваются количеством движения; количество движения переносится от одного тела к другому. Скорость передачи количества движения определяет величину силы взаимодействия. Для каждого из тел в соответствии с (4) можно записать D(m` V)/ Dt =`F. Привести примеры: человек прыгает с лодки и т.д.
10.РАБОТА СИЛЫ И МОЩНОСТЬ. КИНЕТИЧЕСКАЯ И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ. ЗАКОН СОХРАНЕНИЯ И ПРЕВРАЩЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ. Под действием постоянной силы `F тело В может совершить некоторое перемещение Dr. Очевидно, что изменение скорости по модулю и перемещение возможно лишь в том случае, если проекция силы на направление перемещения тела отлична от нуля. Составляющая силы Fcosa называется движущей силой. Нормальная составляющая не вызывает перемещения тела по пути S. Для характеристики перемещающего действия силы вводится
`Fcosa
понитие работы. Работа равна произведению движущей силы на перемещение: DА = |F| |Dr|cosa, т.е. (1) DА = (`F ·D`r) -скалярное произведение векторов силы `F и перемещения D`r. Работа – величина скалярная. Из (1) видно, что при 0<a<900 - работа положительна – сила вызывает перемещение тела; при 900<a<1800 – работа отрицательна – сила препятствует движению тела; при a = 900 – сила не совершает работы по перемещению тела. В частности, центростремительная сила, действующая на тело, равномерно вращающееся по окружности, работы не совершает, т.к. `Fц.с.^` V. Если `F|| D`r, то DА = F Dr. Если тело перемещается под действием нескольких сил, то совершаемая ими работа равна сумме работ всех этих сил (т.е. равна работе результирующей этих сил) DА = åDАi = å(`Fi D`r) (2) Формула (1) применима лишь для вычисления работы постоянной силы на прямолинейном пути. Однако в большинстве случаев траектории движущихся тел криволинейны, а силы, совершающие работу, изменяются по мере движения тел. Чтобы найти работу переменной силы на криволинейном пути, весь путь разбивают на достаточно малые элементы. Каждый из элементов должен быть настолько мал, чтобы его можно было считать приблизительно прямолинейным, а действующую силу - неизменной в любой точке данного элемента пути. (Однако для различных элементов пути силы, вообще говоря, будут различными). Далее, для вычисления работы на каждом из элементов пути уже можно воспользоваться формулой (1). Тогда DАi = Fi Dri cosai. Работа переменной силы на всем криволинейном пути будет: А = åFiDricosai. Поскольку число слогаемых конечное, то получится лишь приблизительная величина работы на пути. Чтобы увеличить точность, необходимо n®µ или Dri®0 и найти предел этой суммы, что практически сводится к операции интегрирования. Следовательно,
А = limå`Fi `Dri = òFcosadr. Dr®o
dS Работу силы на некотором пути S можно определить из графика, дающего зависимость действующей силы от длины проходимого пути S, рис. 2 Действительно, элементарная работа на участке dS будет dA = FsdS - численно равна заштрихованной площади, а работа на всем пути как сумма элементарных работ будет равна сумме площадей всех тонких полосок, т.е. всей площади под кривой. Единицей работы является джоуль. 1 Дж – работа, совершаемая силой 1Н при перемещении тела на расстояние 1м в направлении действия силы. 1Дж = 1 Н·м. Мощность N измеряется отношением работы DА к промежутку времени Dt, за который она совершена: N = DA/Dt. (3) В случае движения тела с постоянной скоростью` V под действием силы `F (преодолевающей сопротивление движению) мощность выражается формулой N = DA/Dt = F Dr/Dt = F V. Если же процесс работы протекает с течением времени неравномерно, то мощность определяется как отношение величины элементарной работы dA к элементарно малому отрезку времени dt, за который эта работа совершается N = dA/dt (мгновенная мощность) В системе СИ единица мощности ватт (Вт). 1Вт – мощность, при которой за время 1с совершается работа 1 Дж. 1 Вт = 1 Дж/с. 1гВт = 100 Вт, 1кВт = 1000 Вт. Мы рассмотрели физическую величину работу силы, которая является количественной мерой передачи движения телу или системе тел. Рассмотрим еще одну физическую величину энергию, которая является количественной мерой движения материальных тел и систем, единой для всех форм движения материи. Процесс работы есть одна из форм передачи энергии от одного тела к другому. Поэтому работа может служить количественной мерой передаваемой энергии, она определяет изменение энергии тела. Именно работа А, приложенной к телу внешней силы, равна изменению энергии этого тела DА = DЕ = Е2 – Е1. (4) Энергия характеризует способность тела или системы тел совершать работу или другими словами, энергия – это запас работы, которую способно совершить тело (или система тел) вследствие того, что оно обладает определенным состоянием движения. Энергия измеряется максимальной работой, которую при определенных (заданных) условиях может совершить эта система (тело). Энергия характеризует состояние системы, способность системы к совершению работы при переходе из одного состояния в другое. Механическая энергия – однозначная функция состояния, т.е. данному состоянию тела соответствует одно и только одно значение его энергии. Для измерения энергии служат те же величины, что и для измерения работы.
КИНЕТИЧЕСКАЯ ЭНЕРГИЯ.
Рис.3.
Используя 2-ой зак. Ньютона и выражение для перемещения при равноускоренном движении, получим DА = mW Dx = mW(V 0t + Wt2/2). (5) Определим время из уравнения V (t) = V 0 + Wt ® t = (V – V0)/W и подставим его в (5)
DА = mW [ V 0(V – V 0)/W + (V – V 0)2/2W2 ] = m V 2(t)/2 – m V 02/2 (6) Величину Ек = m V 2/2 - наз. кинетической энергией. Т.о., работа, совершаемая телом, равна изменению его кинетической энергии. DА = Ек1 – Ек0. Кинетическая энергия увеличивается, когда А > 0 и уменьшается, когда А<0. Например, силы трения совершают А<0. Если в конце рассматриваемого перемещения тело останавлива-ется (V (t) = 0), то совершенная максимальная работа равна кинетической энергии тела в начале перемещения. Значит, работа силы трения является мерой изменения кинетической энергии. Пользуясь уже применявшимся выше приемом разбивки траектории тела на малые отрезки, несложно доказать, что формула (6) справедлива и в общем случае криволинейного пути и переменной силы. Второй вид механической энергии – потенциальная энергия Еп – определяется взаимным положением тел или частиц, находящихся под воздействием сил взаимодействия. Потенциальная энергия – это запас работы, которую могут совершить действующие на тело силы взаимодействия (например, силы тяжести или упругие силы) при перемещении этого тела из данного положения в конечное положение из которого дальнейшее его перемещение под действием тех же сил уже невозможно. Потенциальная энергия тела, занимающего какое-либо положение в пространстве, обычно находится путем вычисления указанной работы действующих на него сил. Только при этом необходимо предварительно установить то конечное состояние тела, в котором его потенциальная энергия принимается равной нулю. В качестве примера определим: 1) потенциальную энергию упругодеформированного тела (стержня). Она равна максимальной работе А, совершаемой силами упругости, восстанавливающими первоначальный размер и форму стержня: Еп = А. Сила упругости равна F = ESD l ¤ l. Эта сила является переменной величиной: она линейно зависит от удлинения D l, изменяясь от нуля при D l = 0 до `F. Поэтому можно считать, что при перемещении D l действует средняя сила упругости <F> = (0 + F)/2 = F/2. Тогда A = <F>D l = F D l ¤2 = ES(D l)2/2 l 0, следовательно Еп = к(D l)2/2, (7) где к = ES/ l - коэффициент пропорциональности в законе Гука. При всех других видах деформации потенциальная энергия тоже пропорциональна квадрату деформации (смещения).
M M m r0 Рис.4. Для этого рассчитаем работу А перемещения первого тела по пути x, соответствующем максимальному сближению тел. Учитывая переменный характер силы тяготения данную задачу просто решить путем интегрирования А = - òFdr = - fmM òdr/r2 = f mM/rп – fmM/r0. (8) А = Епо – Епк, где r – переменное расстояние между центрами тяготеющих масс. Знак (-) потому, что для сближающихся масс dr отрицателен, т.к. работа dA = Fdr должна быть положительной, поскольку перемещение массы происходит в направлении действия силы. Данную задачу можно было решить и без интегрирования, разбивая путь на достаточно малые отрезки, на каждом из которых можно считать силу тяготения постоянной, подсчитать совершаемые на этих отрезках работы и просуммировать их. Но это достаточно громоздко. Из (4) и (6) следует, что Еп = -fMm/r - потенциальная энергия тяготения. Знак (-) показывает, что по мере самопроизвольного сближения тяготеющих тел их потенциальная энергия должна уменьшаться, переходя в кинетическую. В механике доказывается, что всякая предоставленная самой себе система стремится перейти в состояние, соответствующее минимуму потенциальной энергии. Из (7) следует, что максимальное значение кинетической энергии Еп (Wп = 0) тяготеющие тела будут иметь в случае, когда они удалены на r =µ др. от др. и Еп равна min при r®rmin.
|
|||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 546; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.008 с.) |


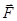
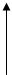



 a В
a В

 В S
В S D`r Рис.1.
D`r Рис.1. Fs
Fs



 Рис.2.
Рис.2. S
S Если под действием постоянной силы `F тело массы m переме-щается на DХ, то сила совершает работу и энергия движущегося тела возрастает на величину проделанной работы. Если тело перемещается по горизонтальной прямой, то m
Если под действием постоянной силы `F тело массы m переме-щается на DХ, то сила совершает работу и энергия движущегося тела возрастает на величину проделанной работы. Если тело перемещается по горизонтальной прямой, то m
 DА = F Dx. `F X
DА = F Dx. `F X

 2) потенциальная энергия тела массы m, находящегося в гравитационном поле другого тела массой М на расстоянии r0 от него.
2) потенциальная энергия тела массы m, находящегося в гравитационном поле другого тела массой М на расстоянии r0 от него.


