
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линии напряженности. Поток вектораСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
НАПРЯЖЁННОСТИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ. Для того, чтобы описать электрическое поле, нужно задать Е в каждой точке поля. Это можно сделать аналитически, выражая зависимость Е(х,у,z) в виде формул. Однако, это можно сделать и графически с помощью так называемых линий напряженности или силовых линий. Силовой линией, или линией вектора напряженности поля, называют линию, проведенную в электрическом поле, для которой направление касательной в любой точке совпадает с направлением вектора напряженности поля (рис.2)
Рис.2 `E
Т.к. касательная определяет два взаимно противоположных направления, то силовой линии приписывают определенное направление, отмечая его на чертеже стрелкой. Густота силовых линий на чертеже отражает величину напряженности поля, а именно, число силовых линий, проходящих через единицу поверхности, перпендикулярной к силовым линиям, равно (или пропорционально) величине напряженности поля в данном месте. Вследствие наглядности графический способ представления полей широко применяют в электротехнике. Из сказанного следует, что силовую линию можно провести через всякую точку поля. Далее, т.к. в каждой точке поля вектор напряженности имеет вполне определенное (одно!) положение, то силовые линии нигде не пересекаются.
В качестве примера рассмотрим картину силовых линий точечного заряда. Для точечного заряда `E||`r и линии напряженности направлены по радиусам, проведённым из заряда. Для положительного заряда (q>0) эти линии исходят из заряда и уходят в ¥ (рис.3 а). Для отрицательного заряда (q<0) `E направлен против радиус-вектора `r, а линии напряженности идут из ¥ и сходятся в точке нахождения заряда (рис.3 б). Как видно из рисунка, густота линий убывает обратно пропорционально квадрату расстояния от заряда, т.е. так же, как и Рис.3. напряженность поля. Т.е. густота линий равна отношению полного числа линий N к величине поверхности сферы радиуса r, т.е. N/4pr2~1/r2. На рис.4 показано электрическое поле между двумя равными по величине точечными зарядами одинаковых и противоположных (рис.5) знаков, расположенными на расстоянии l друг от друга (диполь).
Рис.4. Рис.5. (Дипольный момент Р = q l).
Связь между электрическим полем и его источником может быть выражена достаточно просто. Для этого введём понятие потока вектора напряженности, которое используется при формулировке важнейших свойств электрического, магнитного и других векторных полей. Рассмотрим в пространстве некоторое электрическое поле и замкнутую поверхность произвольной формы. Разделим всю поверхность на столь малые части, что поверхность каждой части (элемента поверхности) можно считать практически плоской; на такой поверхности вектор напряженности электрического поля не будет заметно меняться. Направление элемента поверхности представим вектором нормали. За положительную нормаль к поверхности примем внешнюю нормаль, т.е. нормаль, направленную наружу. Способ разделения поверхности на элементы не имеет значения, пока элементы достаточно малы. Число силовых линий, равных скалярному произведению N = (`E×`n)dSi = Фi - называется потоком вектора напряженности через элемент поверхности dSi. Величина Ф может быть >0 и<0, т.к. нормаль может быть как положительной, так и отрицательной. Теперь сложим потоки через все элементы поверхности и получим поток через всю поверхность Ф = ò (`E×`n)dS =ò (En ×dS, где Еn - проекция `Е на направление нормали к площадке dS, где интеграл берется по поверхности S. Пусть Вас не пугает сложность вычисления таких интегралов для поверхностей сложной формы. Удивительное свойство, которое мы с вами сейчас рассмотрим, делает такие вычисления ненужными! Теорема Остроградского-Гаусса. 1). Возьмём наиболее простой случай: предположим, что поле создано изолированным положительным точечным зарядом q и что поверхностью является сфера радиуса r, в центре которой расположен точечный заряд (Риc. 6). Чему равен поток Ф через такую поверхность?
Рис.6. Ответить на этот вопрос легко, т.к. в каждой точке поверхности `E = (1/4pe0)(q/r3)`r, а поверхность сферы S=4pr2, тогда Ф = E×4pr2= (q/4pe0 r2) 4pr2=q/e0. Как мы видим из этой формулы, поток не зависит от размеров сферы. 2). Покажем теперь, что поток не зависит и от формы поверхности, Напомню, что линии напряженности электрического поля начинаются и заканчиваются только на электрических зарядах. Если замкнутая поверхность не охватывает заряда, то поток вектора электрического поля через эту поверхность равен нулю, т.к. число силовых линий, входящих в поверхность, равно числу выходящих из неё. 3). Пусть поле создается не одним точечным зарядом, а произвольной системой точечных зарядов q1, q2, q3…qn. По принципу суперпозиции напряжённость результирующего электростатического поля равна векторной сумме напряжённостей электростатических полей, создаваемых каждым из зарядов в отдельности: `E = `E1+`E2 +`E3 +…+`En = S`Ei. поэтому проекция вектора `Е на направление нормали к площади dS равна алгебраической сумме проекций всех векторов `Еi на это направление
Поток напряженности результирующего поля сквозь произвольную замкнутую поверхность S, охватывающую заряды q1, q2, …qk, и не охватывающую заряды qk+1…qm, равен поэтому
поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен отношению алгебраической суммы зарядов, охватываемых этой поверхностью, к электрической постоянной. Это и есть теорема Оетроградского -Гаусса применительно к электростатическому полю в вакууме. Теорема Остроградского-Гаусса выведена нами как прямое следствие из закона Кулона. Она позволяет сравнительно просто рассчитывать электрические поля при симметричных распределениях зарядов и окружающих их диэлектриков. Для характеристики электрического поля наряду с `Е удобно ввести ещё одну векторную величину `D, называемую электрическим смещением или электрической индукцией. Для поля в электрически изотропной среде связь `D и `E в СИ имеет вид `D = ee0 `E Тогда к
|
||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 770; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.193.221 (0.009 с.) |


 `E
`E




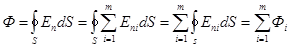 , но Фi=0, если i>k
, но Фi=0, если i>k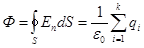 ,т.е.
,т.е.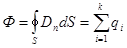 -теорема Остроградского-Гаусса.
-теорема Остроградского-Гаусса.


