Поток вектора электрического смещения сквозь произвольную замкнутую поверхность равен алгебраической сумме электрических зарядов, охватываемых этой поверхностью.

Рассмотрим некоторые простые примеры вычисления электрического поля с помощью теоремы Остроградского-Гаусса.

Пример 1. Равномерно-заряженная плоскость.

Имеется безграничная плоскость, заряженная равномерно с поверхностной плот­ностью заряда s. Найти напряженность Е(х), где х - расстояние до плоскости.

Из симметрии задачи очевидно, что линии напряженности должны быть направлены симметрично в обе стороны от плоскости ^ ей. В этом случае в качестве замкнутой поверхности в теореме Остроградского-Гаусса удобно выбрать прямой цилиндр, перпендикулярный к заряженной плоскости, ограниченный двумя плоскими основаниями, перпендикулярными к силовым линиям и расположенными по обе стороны заряженной плоскости (рис.7).

 

Рис. 7. Рис.8.

Т.к. образующие цилиндра параллельны вектору напряженности электрического поля `Е, то поток через боковую поверхность цилиндра равен нулю и поэтому полный по­ток сквозь цилиндр равен сумме потоков через его основания

Ф =^:2ЕS.

Полный заряд, заключенный внутри цилиндра равен Ss. Поэтому применяя теорему О-Г, имеем:

2ЕS =sS/e₀, откуда

Е = s/2e₀,

т.е. `Е не есть функция расстояния. Следовательно `Е = соnst по величине и по направлению.

Если плотность заряда отрицательная, т.е. (-s), то линии напряжённости имеют противоположное направление.

 

Пример2. Определим поле между двумя плоскостями, равномерно с одинаковой плотностью заряженными разноимёнными зарядами (плоский конденсатор, рис.8). Считаем плоскости бесконечными.

Заряженная плоскость каждой пластины создаст по обе стороны от себя напря­женность поля, выражаемую формулой ±s/2e₀. Внутри металлических пластин и вне конденсатора эти поля направлены противоположно и поэтому в сумме дают нуль. Внутри конденсатора эти поля, напротив, направлены одинаково и, складываясь, дают у поверхности пластин напряженность Е = s/e₀. В данном частном случае электрическое поле од­нородно и поэтому его напряженность у поверхности пластин такая же, как и в других точках поля.

Пример 3. Равномерно заряженный шар.

Рассмотрим электрическое поле между двумя шаровыми концентрическими электродами (рис.9) - шаровой конденсатор. Под действием взаимного притяжения (-) и (+) заря­ды расположатся только на поверхности внутреннего шара и на внутренней поверх­ности внешнего

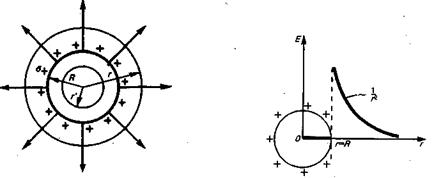
Рис.9. Рис.10.

электрода. Из условий симметрии очевидно, что заряды на обоих ша­ровых электродах будут распределены равномерно, и что линии напряженности электрического поля могут быть только радиальными прямыми. Выберем в качестве замкнутой поверхности сферу с ра­диусом r, расположенную между электродами и имеющую общий центр с обоими элек­тродами.

По теореме Остроградского-Гаусса

Ф = Е(r)4pr² = q/e₀,

откуда

Е(r)=q/4pe₀r². (*)

Эта формула показывает, что напряжённость поля между электродами за­висит от расстояния r рассматриваемой точки поля от центра внутреннего шара, но не зависит вовсе от размеров внешнего электрода. Ту же напряженность поля получим, если радиус внешнего электрода будет как угодно велик. Роль внешнего электрода могут играть различные удалённые заземлённые предметы, например стены, пол и потолок комна­ты. Поэтому часто говорят просто о поле заряженного шара (рис.10), не указывая, что именно является вторым электродом. Из формулы (*) следует, что электрическое поле шара, равномерно заряженного по поверхности, во внешнем про­странстве совпадает с полем точечного заряда, равного полному заряду шара и помещённого в центре шара. Если бы мы рассмотрели шар, заряженный равномерно по объёму, то напряженность поля тоже выражалась бы формулой (*). Напряженность же поля внутри шара в обоих случаях различна. В случае шара, равномерно заряженного по поверхности Е = О в любой внутренней точке. Если же шар заряжен равномерно по объёму, то Е= 0 только в центре шара и с увеличением расстояния r от центра воз­растает пропорционально r. В справедливости этого можно убедиться также при помощи теоремы Остроградского-Гаусса.

 

 

Пример: «клетка Фарадея».

металл

++++++++++++++++

`Е = 0

+ +

+ +

+ +

+ +

+ + + + + + + + + + + + + + +

Рис.11.