
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электроёмкость. Конденсаторы.
Рассмотрим заряженный уединенный проводник, находящийся в неподвижном диэлектрике (вдали от заряженных тел и других проводников). При сообщении ему некоторого заряда последний распределяется по его поверхности с различной плотностью s. Однако характер этого распределения зависит не от общего заряда q, а только от формы проводника. Каждая новая порция зарядов распределяется по поверхности проводника подобно предыдущей. Т.о., s изменяется пропорционально q. Между зарядом проводника q и его потенциалом U существует прямая пропорциональность: q = CU (1) Коэффициент С зависит только от размеров и формы проводника, а также от диэлектрической проницаемости окружающего диэлектрика и ее распределения в пространстве. Он называется емкостью уединённого проводника. Пример: Для уединенного проводящего шара радиуса R, несущего заряд q и находящегося в однородной среде с относительной диэлектрической проницаемостью e потенциал U = q/4pe0eR, oткуда С = 4pe0eR. (2)
Из последней формулы видно, что ни от материала проводника, ни от формы и размеров возможных полостей внутри проводника его электроёмкость не зависит. За единицу электроёмкости в СИ, называемой фарадой (Ф), принимается электроёмкость такого уединённого проводника, потенциал которого изменяется на один вольт при сообщении ему заряда в один кулон: 1Ф=1К/В. Если проводник А не уединённый, т.е. вблизи него имеются другие проводники, то его электроемкость больше, чем у такого же, но уединённого проводника, потому что при сообщении проводнику А заряда q окружающие его проводники заряжаются через влияние. Причём ближайшие к наводящему заряду q оказываются заряды противоположного знака. Эти заряды несколько ослабляют поле, создаваемое зарядом q. Т.о. они понижают потенциал проводника А и повышают его электроёмкость. Наибольший интерес представляет система, состоящая из двух близко расположенных друг от друга проводников, заряды которых численно равны, но противоположны по знаку. Если проводники находятся вдали от каких бы то ни было заряженных тел и иных проводников, то U1-U2= U = q /C, или С = q/U, (3) где С - взаимная электроёмкость двух проводников, зависит от их формы, размеров и взаимного расположения, а также от диэлектрической проницаемости среды.
Важным для практики является случай, когда два разноименно заряженных проводника имеют такую форму и так расположены друг относительно друга, что создаваемое ими электрическое поле полностью или почти полностью сосредоточено в ограниченной части пространства. Такая система проводников называется простым конденсатором или просто конденсатором, а сами проводники - его обкладками. Электроёмкость конденсатора представляет собой взаимную ёмкость его обкладок и выражается формулой (3). В зависимости от формы обкладок конденсаторы делятся на плоские, сферические и цилиндрические. Вычислим емкость плоского конденсатора. Будем считать, что зазор между пластинами мал по сравнению с их размерами, так что краевыми эффектами можно пренебречь. Если поверхностная плотность заряда s и диэлектриком является вакуум, то U=sd/e0, где d - расстояние между пластинами. Но q = sS, поэтому С =q/U = e0S /d. Если диэлектриком является не вакуум, а вещество с диэлектрической проницаемостыо e, заполняющее все пространство, где имеется электрическое поле (пространство между обкладками), то ёмкость будет в e раз больше: С = ee0S/d. При уменьшении расстояния d между пластинами ёмкость увеличивается, что можно наблюдать на опыте. Конденсатор характеризуется не только электроёмкостью, но и так называемым "пробивным напряжением" - разностью потенциалов между его обкладками, при которой может произойти его пробой, т.е. электрический разряд через слой диэлектрика в конденсаторе. Величина пробивного напряжения зависит от свойств диэлектрика, его толщины и формы обкладок.
C3 Рис. 15. Пусть электроёмкость конденсаторов С1, С2,…Сn. В этом случае общим для всех конденсаторов является напряжение U и мы имеем: q1 = С1U, q2= С2 U,… Суммарный заряд, находящийся на батарее, равен q = Sqi = USCi и поэтому емкость батареи C = q/U = SCi. Емкость батареи конденсаторов, соединенных параллельно, равна сумме емкостей отдельных конденсаторов. Допустимое напряжение на батарее будет равно меньшему допустимому напряжению из всех конденсаторов.
Если к концам батареи последовательно соединенных конденсаторов приложить разность потенциалов U, то крайние пластины зарядятся разноименными зарядами ± q. Вследствие электростатической индукции на всех промежуточных пластинах индуцируются заряды, также численно равные ± q, как это показано на рис.16. С1 С2 С3
Рис.16. Т.е. при последовательном соединении одинаковым для всех конденсаторов является заряд q, равный полному заряду батареи, и мы можем записать: U1=q/C1, U2=q/C2 ,… Напряжение же батареи будет равно сумме напряжений на отдельных конденсаторах: U = Поэтому 1/С = S1/Ci При последовательном соединении конденсаторов суммируются обратные величины емкостей. В этом случае напряжение на каждом конденсаторе будет меньше напряжения на батарее, и поэтому допустимое рабочее напряжение батареи будет больше, чем у одного конденсатора. В отдельных случаях используют смешанное соединение конденсаторов.
ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ Если обкладки заряженного конденсатора замкнуть металлической проволокой, то в ней возникает электрический ток, а конденсатор разрядится. Электрический ток разряда конденсатора выделяет в проволоке определённое количество тепла, а это значит, что заряженный конденсатор обладает энергией. Вычислим энергию заряженного конденсатора С. Для этого обозначим через U мгновенное значение напряжения на обкладках конденсатора в процессе разряда. Если малое количество заряда dq проходит в процессе разряда с одной обкладки на другую, то работа электрических сил dА будет dА =U dq. Выражая в этой формуле заряд обкладок qчерез напряжение Q = CU, получим dA = CU dU. Полную работу, совершаемую электрическими силами за все время разряда, равную энергии конденсатора W, мы получим, интегрируя это выражение между значениями напряжения U (начало разряда) и 0 (конец разряда). Это дает: A= - W = C Можно (1) переписать: W = CU2/2 = q2/2C = qU/2. (2) А где именно, т.е. в каком месте в конденсаторе локализована эта энергия? - На обкладках конденсатора, т.е. на электрических зарядах, или в его электрическом поле, т.е. в пространстве между обкладками. В дальнейшем мы сможем ответить на этот вопрос, что энергия сосредоточена в электрическом поле. Дальнейшее развитие теории и эксперимента показало, что переменные во времени электрические и магнитные поля могут существовать обособленно, независимо от возбудивших их зарядов, и распространяются в пространстве в виде электромагнитных волн, способных переносить энергию. Учитывая это, мы можем преобразовать (2) т.о., чтобы в него входила характеристика поля - его напряженность. Рассмотрим вначале однородное поле и применим формулу (1) к плоскому конденсатору. Мы получим W = ee0SU2/2d = ee0(U/d)2Sd/2, но U/d=E, a Sd - объём, занимаемый полем. Мы видим, что энергия однородного электрического поля пропорциональна объёму, занимаемому полем. Поэтому целесообразно говорить об энергии каждой единицы объёма, или об объёмной плотности энергии электрического поля. Она равна W1 = ee0E2/2 = ED/2, т.к. V = Sd = 1.
Последнее выражение справедливо только для изотропного диэлектрика. Если электрическое поле неоднородно, то его можно разбить на элементарные объемы dV и считать, что в пределах бесконечно малого объема это поле однородно. Поэтому энергия, заключенная в объеме поля dV, будет W1dV, а полная энергия любого электрического поля может быть представлена в виде W = (e0/2) Причем интегрирование проводится по всему объему V, где имеется электрическое поле.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 322; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.117.109 (0.02 с.) |

 Для получения больших электроёмкостей конденсаторы соединяют параллельно, рис.15. C1
Для получения больших электроёмкостей конденсаторы соединяют параллельно, рис.15. C1


 1 C2 2
1 C2 2











 +q -q +q -q +q -q
+q -q +q -q +q -q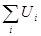 = q
= q 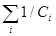 ,
,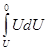 = - CU2/2. (1)
= - CU2/2. (1)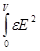 dV,
dV,


