

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Преломление света на сферической поверхности. Формула тонкой линзы.
 площадь треугольника А1ВА2 равна сумме площадей треугольников А1ВО и ОВА2, т.е. с учетом правил знаков площадь треугольника А1ВА2 равна сумме площадей треугольников А1ВО и ОВА2, т.е. с учетом правил знаков 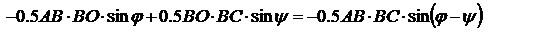 (1). Рассм. только лучи, для которых угол u1 и u2 являются малыми (параксиальные лучи). В таком случае малыми будут также углы (1). Рассм. только лучи, для которых угол u1 и u2 являются малыми (параксиальные лучи). В таком случае малыми будут также углы  и и 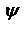 . В параксиальном приближении . В параксиальном приближении    а также A1B»A1S=a1, BA2»SA2=a2. С учетом сделанных приближений, обозначим BO=R, запишем равенство (1) в виде: а также A1B»A1S=a1, BA2»SA2=a2. С учетом сделанных приближений, обозначим BO=R, запишем равенство (1) в виде: 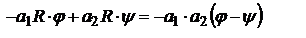 (2). Закон преломления луча АВ в параксиальном приближении имеет вид (2). Закон преломления луча АВ в параксиальном приближении имеет вид  , поэтому после несложных преобразований равенство (2) можно представить в виде соотношения , поэтому после несложных преобразований равенство (2) можно представить в виде соотношения  (3), которое представляет уравнение нулевого луча. Из (3) (3), которое представляет уравнение нулевого луча. Из (3)  , что , что  (4) - нулевым инвариантом Аббе. (4) показывает, что произведение (4) - нулевым инвариантом Аббе. (4) показывает, что произведение  при преломлении (на границе раздела двух сред) сохраняет свою величину. Из (3) и (4) следует, что при заданном значении при преломлении (на границе раздела двух сред) сохраняет свою величину. Из (3) и (4) следует, что при заданном значении  независимо от угла u1 значение независимо от угла u1 значение  определяется однозначно, т.е. для параксиальных лучей гомоцентрический пучок после преломления на сферической границе раздела остается гомоцентрическим. Точка А2 является стигматическим изображением точки А1. Из формулы (3) следует, что, если источник удален от сферической поверхности на бесконечность, т.е. расстояние а1® ¥ то определяется однозначно, т.е. для параксиальных лучей гомоцентрический пучок после преломления на сферической границе раздела остается гомоцентрическим. Точка А2 является стигматическим изображением точки А1. Из формулы (3) следует, что, если источник удален от сферической поверхности на бесконечность, т.е. расстояние а1® ¥ то 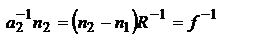 , т.е. , т.е.  . Положение изображения, соответствующее этому случаю называется задним (вторым) фокусом сферической поверхности. Величина, обратная фокусному расстоянию, называется опт. силой преломляющей поверхности. Плоскость, проходящая через фокус перпендикулярно гл. опт. оси, является фокальной плоскостью. Аналогично, при некотором положении источника лучи после преломления на сферической поверхности будут распространяться параллельно опт. оси. В таком случае . Положение изображения, соответствующее этому случаю называется задним (вторым) фокусом сферической поверхности. Величина, обратная фокусному расстоянию, называется опт. силой преломляющей поверхности. Плоскость, проходящая через фокус перпендикулярно гл. опт. оси, является фокальной плоскостью. Аналогично, при некотором положении источника лучи после преломления на сферической поверхности будут распространяться параллельно опт. оси. В таком случае  . Необходимое для этого расстояние от источника до преломляющей поверхности будет равно . Необходимое для этого расстояние от источника до преломляющей поверхности будет равно   Выполнив несложные преобразования, можно получить Выполнив несложные преобразования, можно получить  , учитывая , учитывая  и и  , где , где  и и 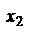 - расстояние от переднего фокуса до предмета и от заднего фокуса до изображения, тогда - расстояние от переднего фокуса до предмета и от заднего фокуса до изображения, тогда  - формула Ньютона. - формула Ньютона. 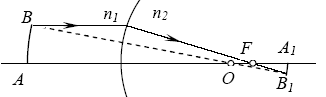 Увеличение. Уравнение Лагранжа-Гельмгольца. Выполним построение изображение небольших предметов при преломлении света на сферической поверхности. Свойства: а) луч, проходящий через оптический центр, не преломляется на сферической поверхности. б) луч, идущий через фокус, после преломления распространяется параллельно опт. оси. в) луч, падающий на сферическую поверхность, после преломления движется параллельно опт. оси. Рассм. сферическую поверхность с центром кривизны в точке О. Пусть точка А, расположенная на опт. оси, является предметом, А1 – ее изображение. Повернем прямую АА1 вокруг центра О на небольшой угол, так что точка А опишет небольшую дугу АВ а точка А1 – дугу А1В1. Так как для всех точек АВ и А1В1 соответствующие расстояния а1 и а2 одинаковы, то можно считать, что А1В1 является изображением дуги АВ. В виду того, что дуги АВ и А1В1 являются очень малыми, то их можно заменить соответствующими хордами. Точно также малая площадка, расположенная перпендикулярно опт. оси, в рассматриваемой сферической опт. системе отобразится при помощи параксиальных лучей в виде площадки, перпендикулярной опт. оси. П лоскость предмета АВ и плоскость его изображения А1В1 являются сопряженными плоскостями по отношению к данной опт. системе. Размер изображения может отличаться от исходного размера предмета. Отношение линейных размеров изображения А1В1 и предмета АВ называется поперечным, или линейным увеличением: Увеличение. Уравнение Лагранжа-Гельмгольца. Выполним построение изображение небольших предметов при преломлении света на сферической поверхности. Свойства: а) луч, проходящий через оптический центр, не преломляется на сферической поверхности. б) луч, идущий через фокус, после преломления распространяется параллельно опт. оси. в) луч, падающий на сферическую поверхность, после преломления движется параллельно опт. оси. Рассм. сферическую поверхность с центром кривизны в точке О. Пусть точка А, расположенная на опт. оси, является предметом, А1 – ее изображение. Повернем прямую АА1 вокруг центра О на небольшой угол, так что точка А опишет небольшую дугу АВ а точка А1 – дугу А1В1. Так как для всех точек АВ и А1В1 соответствующие расстояния а1 и а2 одинаковы, то можно считать, что А1В1 является изображением дуги АВ. В виду того, что дуги АВ и А1В1 являются очень малыми, то их можно заменить соответствующими хордами. Точно также малая площадка, расположенная перпендикулярно опт. оси, в рассматриваемой сферической опт. системе отобразится при помощи параксиальных лучей в виде площадки, перпендикулярной опт. оси. П лоскость предмета АВ и плоскость его изображения А1В1 являются сопряженными плоскостями по отношению к данной опт. системе. Размер изображения может отличаться от исходного размера предмета. Отношение линейных размеров изображения А1В1 и предмета АВ называется поперечным, или линейным увеличением:  . Для перевернутого изображения y1 и y2 имеют различные знаки, поэтому величина . Для перевернутого изображения y1 и y2 имеют различные знаки, поэтому величина  будет отрицательной. Из треугольников АВD и A1B1D имеем будет отрицательной. Из треугольников АВD и A1B1D имеем  , ,  , В параксиальном приближении , В параксиальном приближении  , следовательно , следовательно  , выражение показывает, что поскольку n1 и n2 всегда положительны, то знак увеличения Гл будет определяться отношением , выражение показывает, что поскольку n1 и n2 всегда положительны, то знак увеличения Гл будет определяться отношением 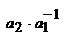 для действительных изображений это отношение будет отрицательным, для мнимых оно положительно. Кроме линейного увеличения опт. с-мы характеризуются угловым увеличением. Угловое увеличение для действительных изображений это отношение будет отрицательным, для мнимых оно положительно. Кроме линейного увеличения опт. с-мы характеризуются угловым увеличением. Угловое увеличение  определяется как отношение тангенсов углов определяется как отношение тангенсов углов  и и  , которые составляют сопряженные лучи с опт. осью с-мы: , которые составляют сопряженные лучи с опт. осью с-мы:  . Поскольку . Поскольку  , получим: , получим:  , это показывает, что угловое увеличение сферической поверхности прямо пропорционально отношению показателя преломления первой среды к показателю преломления второй и обратно пропорционально линейному увеличению. В случае, если все элементы опт. с-мы находятся в одной среде, , это показывает, что угловое увеличение сферической поверхности прямо пропорционально отношению показателя преломления первой среды к показателю преломления второй и обратно пропорционально линейному увеличению. В случае, если все элементы опт. с-мы находятся в одной среде,  и и  Для параксиальных лучей Для параксиальных лучей  и и   и и   - уравнением Лагранжа-Гельмгольца. Уравнение Лагранжа-Гельмгольца справедливо для параксиальных лучей. В случае использования широких пучков условием получения стигматических изображений будет выполнение соотношения - уравнением Лагранжа-Гельмгольца. Уравнение Лагранжа-Гельмгольца справедливо для параксиальных лучей. В случае использования широких пучков условием получения стигматических изображений будет выполнение соотношения  известного как условие синусов Аббе. известного как условие синусов Аббе.
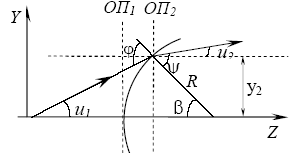
 4.3.Основы матричного метода расчета центрированных опт. систем. Основной задачей геометрической оптики является построение стигматических изображений. т.к. каждая точка изобр. получается в результате схождения нескольких лучей, то решения обозначенной задачи важно уметь опр. ход лучей при их прохождении через опт. с-му. В большинстве случаев опт. с-ма представляет собой совокупность однородных сред, ограниченных плоскими или сферич. границами раздела, на которых происходит преломление, или отр. света. Траектория луча будет предст. Посл. прямых линий, находящихся в одной плоскости. Поэтому будем рассм. только меридиальные лучи, т.е. лучи, распростр. в одной плоскости (в плоскости YZ), проходящей через опт. ось с-мы, вдоль которой направлена ось Z. Для опр-ия хода лучей удобно воспользоваться корд. одной точки, принадл. лучу, и углом, который он составляет с некоторой осью, например, осью Z. Возьмем некоторую плоскость Z=const, перпендикулярную опт. оси и пересекающую рассматриваемый луч. Назовем ее опорной плоскостью ОП1. Любой меридиальный луч можно определить по отношению к опорной плоскости двумя параметрами: высотой y1, на которой рассматриваемы луч пересекает опорную плоскость, и углом u1, который он составляет с осью Z. Как и ранее будем пользоваться правилом знаков: координата y будет положительной, если точка пересечения находится выше оси Z, угол u1 будет положительным, если он соответствует вращению луча по часовой стрелке от положительного направления оси Z к направлению его распространения. Для определения координаты луча в некоторой новой точке необходимо снова провести опорную плоскость ОП2 и определить координаты y2 и u2. П ередаточная матрица. Рассм. вначале распространение света в однородной среде, в которой траектория луча представляет прямую линию. Проведем через точки А и В луча опорные плоскости, соответственно ОП1 и ОП2. Исходными координатами будем считать координаты y1 и u1. Определим координаты луча при его пересечении с опорной плоскостью ОП2, находящейся на расстоянии l от ОП1. 4.3.Основы матричного метода расчета центрированных опт. систем. Основной задачей геометрической оптики является построение стигматических изображений. т.к. каждая точка изобр. получается в результате схождения нескольких лучей, то решения обозначенной задачи важно уметь опр. ход лучей при их прохождении через опт. с-му. В большинстве случаев опт. с-ма представляет собой совокупность однородных сред, ограниченных плоскими или сферич. границами раздела, на которых происходит преломление, или отр. света. Траектория луча будет предст. Посл. прямых линий, находящихся в одной плоскости. Поэтому будем рассм. только меридиальные лучи, т.е. лучи, распростр. в одной плоскости (в плоскости YZ), проходящей через опт. ось с-мы, вдоль которой направлена ось Z. Для опр-ия хода лучей удобно воспользоваться корд. одной точки, принадл. лучу, и углом, который он составляет с некоторой осью, например, осью Z. Возьмем некоторую плоскость Z=const, перпендикулярную опт. оси и пересекающую рассматриваемый луч. Назовем ее опорной плоскостью ОП1. Любой меридиальный луч можно определить по отношению к опорной плоскости двумя параметрами: высотой y1, на которой рассматриваемы луч пересекает опорную плоскость, и углом u1, который он составляет с осью Z. Как и ранее будем пользоваться правилом знаков: координата y будет положительной, если точка пересечения находится выше оси Z, угол u1 будет положительным, если он соответствует вращению луча по часовой стрелке от положительного направления оси Z к направлению его распространения. Для определения координаты луча в некоторой новой точке необходимо снова провести опорную плоскость ОП2 и определить координаты y2 и u2. П ередаточная матрица. Рассм. вначале распространение света в однородной среде, в которой траектория луча представляет прямую линию. Проведем через точки А и В луча опорные плоскости, соответственно ОП1 и ОП2. Исходными координатами будем считать координаты y1 и u1. Определим координаты луча при его пересечении с опорной плоскостью ОП2, находящейся на расстоянии l от ОП1.  , ,  . Будем рассматривать только лучи, составляющие малые углы с осью Z. В этом случае . Будем рассматривать только лучи, составляющие малые углы с осью Z. В этом случае 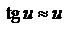 . Кроме того, в матричной оптике вместо углов используется величина . Кроме того, в матричной оптике вместо углов используется величина 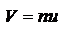 , называемая приведенным углом, т.е. можно переписать , называемая приведенным углом, т.е. можно переписать  , ,  , где , где  , ,  , величина L – приведенная длина. В матричной форме можно записать , величина L – приведенная длина. В матричной форме можно записать  или или 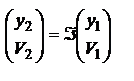 , где , где  . Матрица Á называется передаточной . Матрица Á называется передаточной
 матрицей или матрицей опт. промежутка. Отметим, что матрица Á является унимодулярной, т.е. ее определитель равен единице: матрицей или матрицей опт. промежутка. Отметим, что матрица Á является унимодулярной, т.е. ее определитель равен единице: 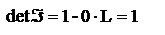 . Рассм. сферическую поверхность, которая разделяет две среды с показателями преломления n1 и n2, а так же имеет радиус кривизны R. Будем R считать положительным, если центр кривизны находится справа от границы раздела и отрицательным, если он находится слева. (Граница раздела сред принимается за начало оси Z). Проведем опорные плоскости 1 OП и 2 OП так, чтобы первая пересекла луч непосредственно перед точкой его падения на границу раздела, а вторая – непосредственно после его преломления. В параксиальном приближении расстояние между ОП1 и ОП2 будет очень малым и поэтому . Рассм. сферическую поверхность, которая разделяет две среды с показателями преломления n1 и n2, а так же имеет радиус кривизны R. Будем R считать положительным, если центр кривизны находится справа от границы раздела и отрицательным, если он находится слева. (Граница раздела сред принимается за начало оси Z). Проведем опорные плоскости 1 OП и 2 OП так, чтобы первая пересекла луч непосредственно перед точкой его падения на границу раздела, а вторая – непосредственно после его преломления. В параксиальном приближении расстояние между ОП1 и ОП2 будет очень малым и поэтому  . Матрица преломления лучей на сферической поверхности. Запишем закон преломления луча на сферической поверхности: . Матрица преломления лучей на сферической поверхности. Запишем закон преломления луча на сферической поверхности:  в параксиальном приближении в параксиальном приближении  . Согласно теореме о внешнем угле треугольника . Согласно теореме о внешнем угле треугольника  , ,  . Умножим эти выражения соответственно на n1 и n2 и запишем с учетом закона преломления . Умножим эти выражения соответственно на n1 и n2 и запишем с учетом закона преломления  . Откуда . Откуда  , ,  , ,  , и в параксиальном приближении , и в параксиальном приближении  , то , то 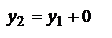 , ,  . Величина . Величина  является опт. силой преломляющей поверхности. В итоге запишем координаты луча при пересечении им ОП2: является опт. силой преломляющей поверхности. В итоге запишем координаты луча при пересечении им ОП2:  , , 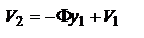 . Представим записанные равенства в матричном виде . Представим записанные равенства в матричном виде  . Матрицу . Матрицу  называют матрицей преломления. Заметим, что, как и в предыдущем случае, определитель матрицы называют матрицей преломления. Заметим, что, как и в предыдущем случае, определитель матрицы  также равен единице: также равен единице:  . Полученный результат может быть использован также для определения координат луча при его преломлении на плоской границе раздела двух сред. В случае плоской поверхности . Полученный результат может быть использован также для определения координат луча при его преломлении на плоской границе раздела двух сред. В случае плоской поверхности 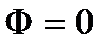 : :  , ,  . В итоге матрица преломления на плоской границе раздела параксиальном приближении будет иметь вид . В итоге матрица преломления на плоской границе раздела параксиальном приближении будет иметь вид  . Центрированной системой называют совокупность опт. элементов, центры кривизны преломляющих и отражающих поверхностей которых расположены на одной прямой, которую называют гл. опт. осью с-мы. Основные элементы опт. с-мы: поверхности (сферические, плоские), которые служат границами раздела и могут быть преломляющими и отражающими; промежутки между ними. матричного метода для определения координат луча при его распространении через толстую линзу. В этом случае следует рассмотреть три опт. элемента: две преломляющие поверхности и промежуток между ними, равный толщине линзы l. Проведем четыре опорные плоскости: причем плоскость ОП1 проведем непосредственно перед передней преломляющей поверхностью. Опорную плоскость ОП2 проведем так, чтобы она пересекала параксиальный луч непосредственно сразу после преломления. Соответственно ОП3 будет проходить через точку падения параксиального луча на вторую преломляющую поверхность. И, наконец, опорную плоскость ОП4 проведем через вершину второй преломляющей поверхности. Именно по отношению к этой плоскости и будем определять координаты выходящего луча. Пусть . Центрированной системой называют совокупность опт. элементов, центры кривизны преломляющих и отражающих поверхностей которых расположены на одной прямой, которую называют гл. опт. осью с-мы. Основные элементы опт. с-мы: поверхности (сферические, плоские), которые служат границами раздела и могут быть преломляющими и отражающими; промежутки между ними. матричного метода для определения координат луча при его распространении через толстую линзу. В этом случае следует рассмотреть три опт. элемента: две преломляющие поверхности и промежуток между ними, равный толщине линзы l. Проведем четыре опорные плоскости: причем плоскость ОП1 проведем непосредственно перед передней преломляющей поверхностью. Опорную плоскость ОП2 проведем так, чтобы она пересекала параксиальный луч непосредственно сразу после преломления. Соответственно ОП3 будет проходить через точку падения параксиального луча на вторую преломляющую поверхность. И, наконец, опорную плоскость ОП4 проведем через вершину второй преломляющей поверхности. Именно по отношению к этой плоскости и будем определять координаты выходящего луча. Пусть  - координаты луча падающего на ОП1, - координаты луча падающего на ОП1, 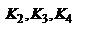 - координаты при пересечении соотв. оп. плоскостей. Пусть Á– матрица опт. промежутка, Â1и Â2- матрицы преломления на 1-й и 2-й сферической поверхности. Ф1 - оптическая сила 1-й поверхности, Ф2 - второй. Если радиусы кривизны поверхностей равны соответственно R1 и R2, то их оптическая сила будет равна - координаты при пересечении соотв. оп. плоскостей. Пусть Á– матрица опт. промежутка, Â1и Â2- матрицы преломления на 1-й и 2-й сферической поверхности. Ф1 - оптическая сила 1-й поверхности, Ф2 - второй. Если радиусы кривизны поверхностей равны соответственно R1 и R2, то их оптическая сила будет равна  и и  . Определим координаты выходящего луча . Определим координаты выходящего луча  . Поскольку . Поскольку  и и  , то , то  и и  - матрица описывающая свойства с-мы. ТО, матрица сложной опт. с-мы равна произведению матриц ее отдельных элементов, записанных в обратном порядке. Можно записать - матрица описывающая свойства с-мы. ТО, матрица сложной опт. с-мы равна произведению матриц ее отдельных элементов, записанных в обратном порядке. Можно записать  . Перемножив: . Перемножив: 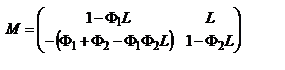 , величина , величина  - опт. сила толстой линзы. - опт. сила толстой линзы.
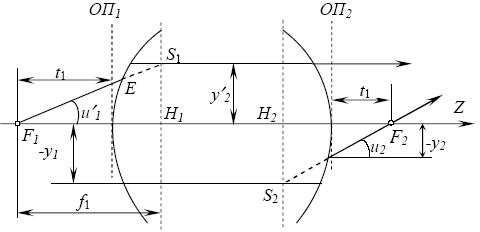 4.4. Кардинальные элементы центрированных опт. систем. Рассм. опт. с-му. Рассм. луч, падающий на опт. с-му параллельно ее опт. оси на некоторой высоте y1. В этом случае 4.4. Кардинальные элементы центрированных опт. систем. Рассм. опт. с-му. Рассм. луч, падающий на опт. с-му параллельно ее опт. оси на некоторой высоте y1. В этом случае 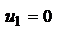 и и 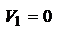 ; Параметры луча на выходе из с-мы, т.е. при его пересечении опорной плоскости ОП2: ; Параметры луча на выходе из с-мы, т.е. при его пересечении опорной плоскости ОП2:  , , 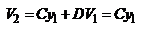 Пусть выходящий луч пересечет опт. ось в точке F2, которая расположена на расстоянии t2 от ОП2, причем Пусть выходящий луч пересечет опт. ось в точке F2, которая расположена на расстоянии t2 от ОП2, причем  , где , где  , тогда параметры можно переписать: , тогда параметры можно переписать:  . Таким образом, t2 не зависит от y1. Это значит, что все параксиальные лучи, которые падают на опт. с-му параллельно ее гл. опт. оси, после прохождения через нее проходят через одну и ту же точку, лежащую на опт. оси, которую принято называть главным задним фокусом опт. с-мы. Если продолжить луч, который входит параллельно гл. опт. оси и луч, который выходит из опт. с-мы, то получим точку S2. Плоскость, проведенная через эту точку . Таким образом, t2 не зависит от y1. Это значит, что все параксиальные лучи, которые падают на опт. с-му параллельно ее гл. опт. оси, после прохождения через нее проходят через одну и ту же точку, лежащую на опт. оси, которую принято называть главным задним фокусом опт. с-мы. Если продолжить луч, который входит параллельно гл. опт. оси и луч, который выходит из опт. с-мы, то получим точку S2. Плоскость, проведенная через эту точку  гл. опт. оси, называют гл. плоскостью. Точка H2 пересечения этой плоскости с гл. опт. осью наз-ся гл. точкой. Фокусным расстоянием опт. с-мы называется расстояние от гл. точки до фокуса, т.е. отрезок гл. опт. оси, называют гл. плоскостью. Точка H2 пересечения этой плоскости с гл. опт. осью наз-ся гл. точкой. Фокусным расстоянием опт. с-мы называется расстояние от гл. точки до фокуса, т.е. отрезок 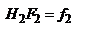 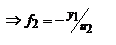 , после преобразований: , после преобразований:  . Таким образом, фокусное расстояние опт. с-мы опр. элементом C матрицы M. опр-им расст. s2 от опорной пл-ти ОП2 до второй гл. пл-ти: . Таким образом, фокусное расстояние опт. с-мы опр. элементом C матрицы M. опр-им расст. s2 от опорной пл-ти ОП2 до второй гл. пл-ти: 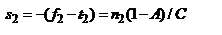 . Проведем луч F1E, под углом u1' к гл. опт. оси с таким расчетом, чтобы после прохождения через опт. с-му он был направлен параллельно гл. опт. оси. В этом случае . Проведем луч F1E, под углом u1' к гл. опт. оси с таким расчетом, чтобы после прохождения через опт. с-му он был направлен параллельно гл. опт. оси. В этом случае  . Поскольку . Поскольку 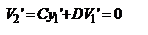 , то , то 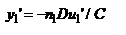 . Определим расстояние t1 от опорной плоскости ОП1 до точки пересечения данного луча с гл. опт. осью с-мы: . Определим расстояние t1 от опорной плоскости ОП1 до точки пересечения данного луча с гл. опт. осью с-мы: 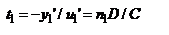 . Полученное соотн. показывает, что t1 не зависит от u1'. Это означает, что все лучи, исходящие из точки F1 после прохождения через опт. с-му будут также || ее гл. опт. оси. Продолжим падающий луч и вышедший до пересечения в точке S1. Плоскость, проходящая через эту точку . Полученное соотн. показывает, что t1 не зависит от u1'. Это означает, что все лучи, исходящие из точки F1 после прохождения через опт. с-му будут также || ее гл. опт. оси. Продолжим падающий луч и вышедший до пересечения в точке S1. Плоскость, проходящая через эту точку  гл. опт. оси, н-ся гл. передней плоскостью. Соответственно точка пересечения этой пл-ти с опт-ой осью Н1 наз-ся гл. первой точкой опт-ой гл. опт. оси, н-ся гл. передней плоскостью. Соответственно точка пересечения этой пл-ти с опт-ой осью Н1 наз-ся гл. первой точкой опт-ой
с-мы. Расст. H1F=f1 наз-ся фокусным расст. опр. переднее фокусное расст.: y2'=-fu1'=-f1V1'/n1 (*) и V2'=0. С другой стороны: 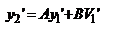 , ,  . Из двух последних равенств: . Из двух последних равенств:  . Учитывая (*): . Учитывая (*):  . Откуда, учитывая свойства унимодулярности матрицы, при котором AD-DC=1, получим: . Откуда, учитывая свойства унимодулярности матрицы, при котором AD-DC=1, получим:  . Расстояние s1 от опорной плоскости ОП1 до передней гл. точки Н1 будет равно: . Расстояние s1 от опорной плоскости ОП1 до передней гл. точки Н1 будет равно:  . Еще 2 кардинальных элемента центр. опт. с-мы: узловые точки и узловые пл-ти. Узловые точки хар-ся св-м: всякий луч, входящий в опт. с-му под углом u1 и проходящий через узловую точку K1, выходит из опт. с-мы под тем же углом к опт. оси, пересекая ее во второй узловой точке K2. Пл-ти, проходящие через узловые точки перпенд. гл. опт. оси, наз-ся узловыми пл-ми. Обозначим через h1 расстояние от опорной плоскости ОП1 до точки K1 и соответств. расст. от опорной плоскости ОП2 до K2 - через – h2. Запишем матрицу . Еще 2 кардинальных элемента центр. опт. с-мы: узловые точки и узловые пл-ти. Узловые точки хар-ся св-м: всякий луч, входящий в опт. с-му под углом u1 и проходящий через узловую точку K1, выходит из опт. с-мы под тем же углом к опт. оси, пересекая ее во второй узловой точке K2. Пл-ти, проходящие через узловые точки перпенд. гл. опт. оси, наз-ся узловыми пл-ми. Обозначим через h1 расстояние от опорной плоскости ОП1 до точки K1 и соответств. расст. от опорной плоскости ОП2 до K2 - через – h2. Запишем матрицу  преобразования лучей между узловыми плоскостями: преобразования лучей между узловыми плоскостями:  , где , где  , , 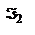 - передаточные матрицы смещения лучей между опорными и узловыми плоскостями: - передаточные матрицы смещения лучей между опорными и узловыми плоскостями:  , ,  . 1ое во 2ое, получим: . 1ое во 2ое, получим: 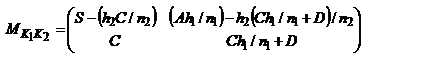 . можно упросить. Запишем координаты луча y2 и V2 при пересечении им второй узловой плоскости, считая заданными его координаты y1 и V1 при пересечении передней узловой плоскости: . можно упросить. Запишем координаты луча y2 и V2 при пересечении им второй узловой плоскости, считая заданными его координаты y1 и V1 при пересечении передней узловой плоскости: 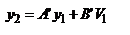 , , 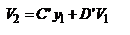 . Поскольку узловые точки расположены на гл. опт. оси, то . Поскольку узловые точки расположены на гл. опт. оси, то  , соответственно , соответственно  . Это возможно если . Это возможно если 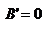 . Далее, на основании свойства узловых точек . Далее, на основании свойства узловых точек 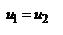 или или  , можем записать (при , можем записать (при  ): ):  Используя записанные условия, получим Используя записанные условия, получим  и и  , покажем, что расстояние между узлами всегда равно расстоянию между главными точками. Действительно, расстояние между узлами, расстояние К1К2 с учетом правила знаков будет равно: , покажем, что расстояние между узлами всегда равно расстоянию между главными точками. Действительно, расстояние между узлами, расстояние К1К2 с учетом правила знаков будет равно:  . Или, принимая во внимание выражения для h1 и h2, запишем . Или, принимая во внимание выражения для h1 и h2, запишем 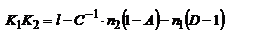 . Точно такой результат получается и для расстояния . Точно такой результат получается и для расстояния 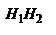 . В случае, если опт. св-ва среды по обе стороны с-мы одинаковы . В случае, если опт. св-ва среды по обе стороны с-мы одинаковы  , то узловые точки совпадают с гл. Фокусное расст. опт. с-мы (опт. сила) определяются элементом С. Заметим, что при , то узловые точки совпадают с гл. Фокусное расст. опт. с-мы (опт. сила) определяются элементом С. Заметим, что при  имеем:, имеем:,  т.е. переднее фокусное расст. равно заднему фокусному расст. При т.е. переднее фокусное расст. равно заднему фокусному расст. При  : :  . Точки F1 и F2, H1 и H2, K1 и K2 а так же плоскости, которые проходят через них перпендикулярно гл. опт. оси, называются кардинальными. MН преобразования лучей между передней H1 и задней H2 гл. плоскостями: . Точки F1 и F2, H1 и H2, K1 и K2 а так же плоскости, которые проходят через них перпендикулярно гл. опт. оси, называются кардинальными. MН преобразования лучей между передней H1 и задней H2 гл. плоскостями:  , где , где  - матрица опт. промежутка от Н2 до ОП2 толщиной s2, M – матрица преобразования лучей между ОП2 ОП1, - матрица опт. промежутка от Н2 до ОП2 толщиной s2, M – матрица преобразования лучей между ОП2 ОП1,  - матрица опт. промежутка от ОП1 до H2. Подставив всё в MH: - матрица опт. промежутка от ОП1 до H2. Подставив всё в MH:  , перемножив и учитывая св-ва унимодулярности: , перемножив и учитывая св-ва унимодулярности:  . Поскольку A=1, B=0, то . Поскольку A=1, B=0, то 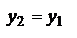 , ,  сопряжённые точки, на гл. плоскостях отображаются с линейным увеличением, равным ед., т.е. любой луч, который проходит через плоскость H1, пересечет H2 на той же высоте. матрицу преобразования лучей между двумя фокальными плоскостями F1 и о F2: сопряжённые точки, на гл. плоскостях отображаются с линейным увеличением, равным ед., т.е. любой луч, который проходит через плоскость H1, пересечет H2 на той же высоте. матрицу преобразования лучей между двумя фокальными плоскостями F1 и о F2:  , здесь , здесь  , , 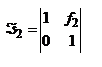 , перемножив: , перемножив:  все все
параллельные лучи, которые пересекают переднюю фокальную плоскость на различной высоте, после преобразования опт. системой проходят через заднюю фокальную плоскость в одной точке.
  4.5 Аберрации опт. Систем. Место схожд. стигматического пучка наз-ся фокусом. Его волновая пов-ть является сферической. Астигматическим называется пучок, не имеющий точки схождения. Поверхность астигматического пучка несферическая. Параксиальный пучок при прохождении через центрированную опт. с-му остается гомоцентрическим. Центрированная оптическая с-ма при использовании параксиальных лучей дает стигматическое изображение. Однако параксиальный пучок является идеализацией. В практической оптике используются широкие непараксиальные пучки, которые к тому же являются немонохром. Это приводит к тому, что получаемое изобр. уже не будет полностью геом. подобным предмету, т.е. будут возникать искажения изобр-ия. В таком случае говорят, что опт. с-ма обладает погрешностями, т.е. аберрациями. В общем случае: аберрация - любое нарушение гомоцентричности светового пучка вызванное его прохожд. через опт. с-му. Аберрации опт. с-м бывают монохром. и хроматические. Монохром.аберрации возникают при прохождении монохром. непараксиальных пучков через опт. с-му. Хроматические аберрации имеют место при использовании немонохром. пучков света. Вследствие явления дисперсии света коэфф. преломления, а, следовательно, и точка схождения лучей различной длины, будут различными. Это приводит к тому, что даже при отсутствии монохроматических аберрации, изображение, получаемое в белом свете, будет окрашенным. Процесс устранения аберраций опт. с-мы называется корригированием. Полностью устранить аберрации нельзя, но можно уменьшить до нужной величины. Например, при рассм. предмета визуально, или с помощью опт. прибора размер аберрации должен быть меньше min разрешаемого ими геом. размера. В этом случае аберрации не будут влиять на качество изобр. Рассм. монохром. аберрации. Одной из наиболее часто встречаемых аберраций является сферическая аберрация. возникает при отображении широким пучком точек, лежащих на опт. оси. рассм. точечный объект А, расположенный на опт. оси. Из всей совокупности лучей, падающих на линзу, выделим 2 пары: 1-1' и 2-2'. Для 1ой углы падения на преломляющую пов-ть являются малыми, и параксиальное приближение выполняется с большой точностью. Эти лучи образуют стигматическое изобр. в точке А1. Для второй пары лучей углы падения будут больше чем для параксиальных лучей, поэтому и углы преломл. также будут больше. Это приведет к тому, что они пересекут опт.ось в точке А2, расположенной ближе к линзе. Наблюдая изобр. на экране, заметим, что ни при каком его положении не получится точечное изобр. если расположить экран перпенд. опт. оси так, чтобы он проходил через точку А1, то изобр. будет иметь вид яркой точки в центре, окруженной светлым ореолом, к-ый наз-т кружком рассеяния. Центр изобр. будут создавать параксиальные лучи; кружок рассеяния будут создавать непаракс. лучи. Вблизи точки А1 имеется зона max концентрации световой энергии. Поверхность, огибающая эту область пространства, называется каустической поверхностью, или каустикой. В сечении каустика представляет геом. место точек схождения меридиональных лучей. Сферическая аберрация х-ся разностью коорд. точек A1 и A2: δs=OA1-OA2. Это разность называется продольной аберрацией. Продольная аберрация считается (+), если точка А2 расположена правее точки А1 и (-) – если точка А2 расположена левее А1. В приведенном на рис. примере продольная аберрация будет (-). Кроме величины δs продольная аберрация характеризуется величиной δs =CD - размером кружка рассеяния на экране, расположенном в плоскости параксиального изображения, вдоль направления перпенд. опт. оси. Собирающая линза имеет отрицательную аберрацию продольную аберрацию, рассеивающая – положительную. Размер продольной и поперечной аберрации зависит от апертуры пучка, падающего на линзу. Осуществляя диафрагмирование пучка, можно значительно уменьшить сферическую аберрацию. Однако, диафрагмирование приводит к уменьшению освещенности изображения. Кроме того, в случае микроскопа уменьшение апертуры нежелательно еще и потому, что это уменьшает их разрешающую способность. Сферическую аберрацию можно в значительной мере уменьшить, используя комбинацию из нескольких собирающих и рассеивающих линз. Аберрация кома. Часто источник, посылающий на линзу широкий пучок, расположен вне опт. оси. В этом случае каустика не имеет осевой симметрии. Она симм. отн-но меридиональной плоскости и по форме напоминает комету с хвостом. Такой вид погрешности опт. систем называется аберрацией кома. В отличие от сферической аберрации, кома определяется не только сферичностью поверхности линзы, но удаленностью от опт. оси с-мы. Действительно, при наклонном падении широкого пучка на линзу его верхние и нижние лучи преломляются по-разному. В итоге широкий параллельный пучок дает на экране не точечное изображение, а пятно довольно сложной формы. Кома является одной из наиболее существенных аберраций, особенно в микроскопии, где используют широкие пучки. Аберрация кома полностью устраняется при выполнении условия: y1n1sinu1= y2n2sinu2, где y1, y2 - размер предмета и изображения, u1, u2 - апертура лучей падающих на объектив и лучей, форм. изобр. это усл-ие синусов Аббе, может быть получено как следствие физического требования в соответствии, с которым для получения стигматического изобр. необходимо, чтобы опт. длина путей между сопряженными точками предмета и изображения были одинаковыми. Точки, для которых устранена сферическая аберрация и выполнено условие синусов Аббе, наз-ся апланатическими. Получаемые при этом изображения также называются апланатическими. Опт. с-ма может давать апланатическое изобр. только при опр. расст. до предмета и изобр.. Это усл-ие выполняется в микроскопе, где предмет всегда располагается в одной плоскости, находящейся вблизи фокальной плоскости. Причиной хроматической аберрации является явление дисперсии света в веществе, из которого изготовлена линза. 4.5 Аберрации опт. Систем. Место схожд. стигматического пучка наз-ся фокусом. Его волновая пов-ть является сферической. Астигматическим называется пучок, не имеющий точки схождения. Поверхность астигматического пучка несферическая. Параксиальный пучок при прохождении через центрированную опт. с-му остается гомоцентрическим. Центрированная оптическая с-ма при использовании параксиальных лучей дает стигматическое изображение. Однако параксиальный пучок является идеализацией. В практической оптике используются широкие непараксиальные пучки, которые к тому же являются немонохром. Это приводит к тому, что получаемое изобр. уже не будет полностью геом. подобным предмету, т.е. будут возникать искажения изобр-ия. В таком случае говорят, что опт. с-ма обладает погрешностями, т.е. аберрациями. В общем случае: аберрация - любое нарушение гомоцентричности светового пучка вызванное его прохожд. через опт. с-му. Аберрации опт. с-м бывают монохром. и хроматические. Монохром.аберрации возникают при прохождении монохром. непараксиальных пучков через опт. с-му. Хроматические аберрации имеют место при использовании немонохром. пучков света. Вследствие явления дисперсии света коэфф. преломления, а, следовательно, и точка схождения лучей различной длины, будут различными. Это приводит к тому, что даже при отсутствии монохроматических аберрации, изображение, получаемое в белом свете, будет окрашенным. Процесс устранения аберраций опт. с-мы называется корригированием. Полностью устранить аберрации нельзя, но можно уменьшить до нужной величины. Например, при рассм. предмета визуально, или с помощью опт. прибора размер аберрации должен быть меньше min разрешаемого ими геом. размера. В этом случае аберрации не будут влиять на качество изобр. Рассм. монохром. аберрации. Одной из наиболее часто встречаемых аберраций является сферическая аберрация. возникает при отображении широким пучком точек, лежащих на опт. оси. рассм. точечный объект А, расположенный на опт. оси. Из всей совокупности лучей, падающих на линзу, выделим 2 пары: 1-1' и 2-2'. Для 1ой углы падения на преломляющую пов-ть являются малыми, и параксиальное приближение выполняется с большой точностью. Эти лучи образуют стигматическое изобр. в точке А1. Для второй пары лучей углы падения будут больше чем для параксиальных лучей, поэтому и углы преломл. также будут больше. Это приведет к тому, что они пересекут опт.ось в точке А2, расположенной ближе к линзе. Наблюдая изобр. на экране, заметим, что ни при каком его положении не получится точечное изобр. если расположить экран перпенд. опт. оси так, чтобы он проходил через точку А1, то изобр. будет иметь вид яркой точки в центре, окруженной светлым ореолом, к-ый наз-т кружком рассеяния. Центр изобр. будут создавать параксиальные лучи; кружок рассеяния будут создавать непаракс. лучи. Вблизи точки А1 имеется зона max концентрации световой энергии. Поверхность, огибающая эту область пространства, называется каустической поверхностью, или каустикой. В сечении каустика представляет геом. место точек схождения меридиональных лучей. Сферическая аберрация х-ся разностью коорд. точек A1 и A2: δs=OA1-OA2. Это разность называется продольной аберрацией. Продольная аберрация считается (+), если точка А2 расположена правее точки А1 и (-) – если точка А2 расположена левее А1. В приведенном на рис. примере продольная аберрация будет (-). Кроме величины δs продольная аберрация характеризуется величиной δs =CD - размером кружка рассеяния на экране, расположенном в плоскости параксиального изображения, вдоль направления перпенд. опт. оси. Собирающая линза имеет отрицательную аберрацию продольную аберрацию, рассеивающая – положительную. Размер продольной и поперечной аберрации зависит от апертуры пучка, падающего на линзу. Осуществляя диафрагмирование пучка, можно значительно уменьшить сферическую аберрацию. Однако, диафрагмирование приводит к уменьшению освещенности изображения. Кроме того, в случае микроскопа уменьшение апертуры нежелательно еще и потому, что это уменьшает их разрешающую способность. Сферическую аберрацию можно в значительной мере уменьшить, используя комбинацию из нескольких собирающих и рассеивающих линз. Аберрация кома. Часто источник, посылающий на линзу широкий пучок, расположен вне опт. оси. В этом случае каустика не имеет осевой симметрии. Она симм. отн-но меридиональной плоскости и по форме напоминает комету с хвостом. Такой вид погрешности опт. систем называется аберрацией кома. В отличие от сферической аберрации, кома определяется не только сферичностью поверхности линзы, но удаленностью от опт. оси с-мы. Действительно, при наклонном падении широкого пучка на линзу его верхние и нижние лучи преломляются по-разному. В итоге широкий параллельный пучок дает на экране не точечное изображение, а пятно довольно сложной формы. Кома является одной из наиболее существенных аберраций, особенно в микроскопии, где используют широкие пучки. Аберрация кома полностью устраняется при выполнении условия: y1n1sinu1= y2n2sinu2, где y1, y2 - размер предмета и изображения, u1, u2 - апертура лучей падающих на объектив и лучей, форм. изобр. это усл-ие синусов Аббе, может быть получено как следствие физического требования в соответствии, с которым для получения стигматического изобр. необходимо, чтобы опт. длина путей между сопряженными точками предмета и изображения были одинаковыми. Точки, для которых устранена сферическая аберрация и выполнено условие синусов Аббе, наз-ся апланатическими. Получаемые при этом изображения также называются апланатическими. Опт. с-ма может давать апланатическое изобр. только при опр. расст. до предмета и изобр.. Это усл-ие выполняется в микроскопе, где предмет всегда располагается в одной плоскости, находящейся вблизи фокальной плоскости. Причиной хроматической аберрации является явление дисперсии света в веществе, из которого изготовлена линза. 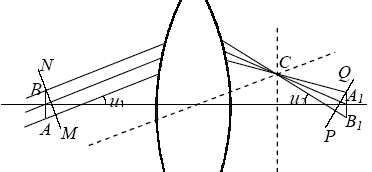 Действительно, фокусное расстояние тонкой линзы определяется выражением Действительно, фокусное расстояние тонкой линзы определяется выражением 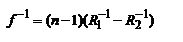
 Хроматическая аберрация. Ахроматизация линз., продифф.: Хроматическая аберрация. Ахроматизация линз., продифф.:  или или  , где , где 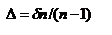 - отн-ая дисперсия. Если световой пучок, падающий на линзу, является немонохром., то при изменении длины волны величина - отн-ая дисперсия. Если световой пучок, падающий на линзу, является немонохром., то при изменении длины волны величина  , т.е. , т.е.  и фокусное расстояние для волн различной длины будет различным. Это приводит к тому, что положение изображения в немонохроматическом свете будет различным, т.е. к хроматической аберрации. Если используются две линзы, сложенные вплотную, то фокусное расстояние такой опт. с-мы будет равно и фокусное расстояние для волн различной длины будет различным. Это приводит к тому, что положение изображения в немонохроматическом свете будет различным, т.е. к хроматической аберрации. Если используются две линзы, сложенные вплотную, то фокусное расстояние такой опт. с-мы будет равно  , продифференцировав: , продифференцировав: 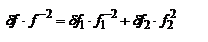 , решив: , решив:  Для ахроматизации, т.е. исчезновения хроматической аберрации, необходимо выполнение условия Для ахроматизации, т.е. исчезновения хроматической аберрации, необходимо выполнение условия  или или  - Это усл-ие может быть выполнено, только если слагаемые имеют различные знаки. Поскольку - Это усл-ие может быть выполнено, только если слагаемые имеют различные знаки. Поскольку  и и 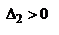 (линзы работают в области нормальной дисперсии), то для выполнения условия необходимо, чтобы различные знаки имели f1 и f2, т.е. одна линза должна быть собирающей, а другая - рассеивающей. Пусть f1>0, f2<0, Если ахроматический объектив должен обладать положительной опт. силой, т.е. быть собирающим, то необходимо, чтобы (линзы работают в области нормальной дисперсии), то для выполнения условия необходимо, чтобы различные знаки имели f1 и f2, т.е. одна линза должна быть собирающей, а другая - рассеивающей. Пусть f1>0, f2<0, Если ахроматический объектив должен обладать положительной опт. силой, т.е. быть собирающим, то необходимо, чтобы  , и , и  . ТО, ахроматической объектив можно изготовить из двух линз, сложенных вплотную: собирающей и рассеивающей, если он должен иметь (+) опт. силу, то первую линзу необходимо изготовить из материала, обладающего большей отн-ой дисперсией. Если фокусное расст. ахроматического объектива известно, то можно определить f1 и f2: . ТО, ахроматической объектив можно изготовить из двух линз, сложенных вплотную: собирающей и рассеивающей, если он должен иметь (+) опт. силу, то первую линзу необходимо изготовить из материала, обладающего большей отн-ой дисперсией. Если фокусное расст. ахроматического объектива известно, то можно определить f1 и f2:  , ,  . Значения f1 и f2 достигаются подбором радиусов кривизны сферических пов-тей линз . Значения f1 и f2 достигаются подбором радиусов кривизны сферических пов-тей линз 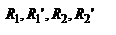 . Опт. с-мы, у которых устранена хроматическая аберрация, наз-ся ахроматизироваными. Следует заметить, что полностью устранить хроматическую аберрацию невозможно. Обычно ее устраняют для какой-либо опр. спектральной обл. В приборах, предназначенных для визуальных наблюдений, это обычно желто-зеленая область. Хроматическая аберрация является крайне нежелательной в микроскопах. Поэтому их составные части являются ахроматизироваными. Объективы, у которых ахроматизация выполнена для двух цветов спектра называют ахроматами. Однако во многих случаях, которые имеют место в микроскопии, такой ахроматизации недостаточно. Аббе определил условия, при которых достигается ахроматизация объективов для трех длин волн. Такие объективы наз-ся апохроматами. Апохроматы широко используются в опт. микроскопах. Астигматизм наклонных пучков и кривизна поля. Даже узкие пучки утрачивают гомоцентричность при прохождении через опт. с-му, если они составляют с опт. осью значительные углы. Для того, чтобы наглядно представить характер искажений, возникающих в этом случае, введем несколько опр. Плоскость, проходящую через опт. ось с-мы и центральный луч падающего пучка, наз-ся меридианальной. Часто эта плоскость совмещается с плоскостью рисунка. Плоскость, перпенд. меридианальной плоскости и также содержащая центральный луч, наз-ся саггитальной. Рассм. гомоцентрический узкий пучок света, исходящий из точки А и падающий на опт. с-му под углом к ее гл. опт. оси. Пусть mm и ss – сечения линзы меридианальной и саггитальной плоскостью соответственно. Вследствие различия радиусов кривизны преломляющих пов-ей в этих взаимно перпенд. сечениях, волновая пов-ть пучка после преломления будет не сферической. Меридианальные лучи пересекаться на фокальной линии Рm, расположенной в саггитальной плоскости, саггитальные лучи на линии Рs, расположенной в меридианальной плоскости. Расстояние между этими линиями, которое мы опр-ли как астигматическая разность, быстро возрастает с увеличением угла между пучком и опт. осью. Такой вид аберрации наз-ся астигматизмом. Астигматизм приводит к искривлению поля изобр., т.е. изобр. даже плоской фигуры оказывается не совсем резким на плоскости. Астигматизм крайне нежелателен для фотообъективов, которые должны давать резкие изобр. на плоскости пленки и светочувствительной матрицы. Комбинируя линзы с различным радиусом кривизны пов-ти и фокусными расст., можно приблизительно совместить меридианальные и саггитальные фокальные линии, сделав их практически прямыми. Опт. с-мы, у которых исправлена аберрация астигматизма, называются анастигматами. . Опт. с-мы, у которых устранена хроматическая аберрация, наз-ся ахроматизироваными. Следует заметить, что полностью устранить хроматическую аберрацию невозможно. Обычно ее устраняют для какой-либо опр. спектральной обл. В приборах, предназначенных для визуальных наблюдений, это обычно желто-зеленая область. Хроматическая аберрация является крайне нежелательной в микроскопах. Поэтому их составные части являются ахроматизироваными. Объективы, у которых ахроматизация выполнена для двух цветов спектра называют ахроматами. Однако во многих случаях, которые имеют место в микроскопии, такой ахроматизации недостаточно. Аббе определил условия, при которых достигается ахроматизация объективов для трех длин волн. Такие объективы наз-ся апохроматами. Апохроматы широко используются в опт. микроскопах. Астигматизм наклонных пучков и кривизна поля. Даже узкие пучки утрачивают гомоцентричность при прохождении через опт. с-му, если они составляют с опт. осью значительные углы. Для того, чтобы наглядно представить характер искажений, возникающих в этом случае, введем несколько опр. Плоскость, проходящую через опт. ось с-мы и центральный луч падающего пучка, наз-ся меридианальной. Часто эта плоскость совмещается с плоскостью рисунка. Плоскость, перпенд. меридианальной плоскости и также содержащая центральный луч, наз-ся саггитальной. Рассм. гомоцентрический узкий пучок света, исходящий из точки А и падающий на опт. с-му под углом к ее гл. опт. оси. Пусть mm и ss – сечения линзы меридианальной и саггитальной плоскостью соответственно. Вследствие различия радиусов кривизны преломляющих пов-ей в этих взаимно перпенд. сечениях, волновая пов-ть пучка после преломления будет не сферической. Меридианальные лучи пересекаться на фокальной линии Рm, расположенной в саггитальной плоскости, саггитальные лучи на линии Рs, расположенной в меридианальной плоскости. Расстояние между этими линиями, которое мы опр-ли как астигматическая разность, быстро возрастает с увеличением угла между пучком и опт. осью. Такой вид аберрации наз-ся астигматизмом. Астигматизм приводит к искривлению поля изобр., т.е. изобр. даже плоской фигуры оказывается не совсем резким на плоскости. Астигматизм крайне нежелателен для фотообъективов, которые должны давать резкие изобр. на плоскости пленки и светочувствительной матрицы. Комбинируя линзы с различным радиусом кривизны пов-ти и фокусными расст., можно приблизительно совместить меридианальные и саггитальные фокальные линии, сделав их практически прямыми. Опт. с-мы, у которых исправлена аберрация астигматизма, называются анастигматами.
4.6. Оптические приборы: лупа, микроскоп, телескоп. Оптическая схема увеличение. Чувствительность глаза:Палочки содержат пигмент с максимальной чувствительностью на длине волны около 510 нм (точечная линия на рисунке), в зеленой части спектра. Суммарная кривая спектральной чувствительности глаза для случая яркого освещения, т.е. цветного зрения, показана на рисунке сплошной линией.  Колбочек существует три типа отличающихся фоточувствительным пигментом. Колбочки обычно называют "синими", "зелеными" и "красными" в соответствии с наименованием цвета, для которого они оптимально чувствительны. Упомянутые три пигмента имеют максимальные поглощения приблизительно на 430, 530 и 560 нм. Этим длинам волн соответствует фиолетовый, сине-зеленый и желто-зеленый. Бинокулярное зрение: вырабатывавшаяся тысячелетиями, согласованная работа глаз постепенно создала новое чувство или ощущение глубины или рельефа, обусловливаемое двумя обстоятельствами: 1) непараллельностью (конвергенцией) оптических осей, направленных на наблюдаемый предмет 2) неодинаковостью изображений, получаемых на обеих сетчатках. Лупа: Лупа - простейшая оптическая система с фокусным расстоянием 100¸10 мм. Колбочек существует три типа отличающихся фоточувствительным пигментом. Колбочки обычно называют "синими", "зелеными" и "красными" в соответствии с наименованием цвета, для которого они оптимально чувствительны. Упомянутые три пигмента имеют максимальные поглощения приблизительно на 430, 530 и 560 нм. Этим длинам волн соответствует фиолетовый, сине-зеленый и желто-зеленый. Бинокулярное зрение: вырабатывавшаяся тысячелетиями, согласованная работа глаз постепенно создала новое чувство или ощущение глубины или рельефа, обусловливаемое двумя обстоятельствами: 1) непараллельностью (конвергенцией) оптических осей, направленных на наблюдаемый предмет 2) неодинаковостью изображений, получаемых на обеих сетчатках. Лупа: Лупа - простейшая оптическая система с фокусным расстоянием 100¸10 мм.  , где , где 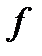 - фокусное расстояние лупы. - фокусное расстояние лупы.
 К расчету увеличения лупы. Микроскоп: Первый микроскоп был построен голландским мастером Янсеном. Первое удачное применение микроскопа в научных исследованиях связано с именем английского ученого Гука (1665 г.), котор К расчету увеличения лупы. Микроскоп: Первый микроскоп был построен голландским мастером Янсеном. Первое удачное применение микроскопа в научных исследованиях связано с именем английского ученого Гука (1665 г.), котор
|



 площадь треугольника А1ВА2 равна сумме площадей треугольников А1ВО и ОВА2, т.е. с учетом правил знаков
площадь треугольника А1ВА2 равна сумме площадей треугольников А1ВО и ОВА2, т.е. с учетом правил знаков 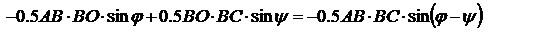 (1). Рассм. только лучи, для которых угол u1 и u2 являются малыми (параксиальные лучи). В таком случае малыми будут также углы
(1). Рассм. только лучи, для которых угол u1 и u2 являются малыми (параксиальные лучи). В таком случае малыми будут также углы  и
и 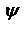 . В параксиальном приближении
. В параксиальном приближении 

 а также A1B»A1S=a1, BA2»SA2=a2. С учетом сделанных приближений, обозначим BO=R, запишем равенство (1) в виде:
а также A1B»A1S=a1, BA2»SA2=a2. С учетом сделанных приближений, обозначим BO=R, запишем равенство (1) в виде: 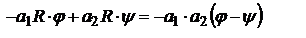 (2). Закон преломления луча АВ в параксиальном приближении имеет вид
(2). Закон преломления луча АВ в параксиальном приближении имеет вид 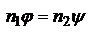 , поэтому после несложных преобразований равенство (2) можно представить в виде соотношения
, поэтому после несложных преобразований равенство (2) можно представить в виде соотношения  (3), которое представляет уравнение нулевого луча. Из (3)
(3), которое представляет уравнение нулевого луча. Из (3)  , что
, что  (4) - нулевым инвариантом Аббе. (4) показывает, что произведение
(4) - нулевым инвариантом Аббе. (4) показывает, что произведение  при преломлении (на границе раздела двух сред) сохраняет свою величину. Из (3) и (4) следует, что при заданном значении
при преломлении (на границе раздела двух сред) сохраняет свою величину. Из (3) и (4) следует, что при заданном значении  независимо от угла u1 значение
независимо от угла u1 значение  определяется однозначно, т.е. для параксиальных лучей гомоцентрический пучок после преломления на сферической границе раздела остается гомоцентрическим. Точка А2 является стигматическим изображением точки А1. Из формулы (3) следует, что, если источник удален от сферической поверхности на бесконечность, т.е. расстояние а1® ¥ то
определяется однозначно, т.е. для параксиальных лучей гомоцентрический пучок после преломления на сферической границе раздела остается гомоцентрическим. Точка А2 является стигматическим изображением точки А1. Из формулы (3) следует, что, если источник удален от сферической поверхности на бесконечность, т.е. расстояние а1® ¥ то 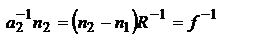 , т.е.
, т.е.  . Положение изображения, соответствующее этому случаю называется задним (вторым) фокусом сферической поверхности. Величина, обратная фокусному расстоянию, называется опт. силой преломляющей поверхности. Плоскость, проходящая через фокус перпендикулярно гл. опт. оси, является фокальной плоскостью. Аналогично, при некотором положении источника лучи после преломления на сферической поверхности будут распространяться параллельно опт. оси. В таком случае
. Положение изображения, соответствующее этому случаю называется задним (вторым) фокусом сферической поверхности. Величина, обратная фокусному расстоянию, называется опт. силой преломляющей поверхности. Плоскость, проходящая через фокус перпендикулярно гл. опт. оси, является фокальной плоскостью. Аналогично, при некотором положении источника лучи после преломления на сферической поверхности будут распространяться параллельно опт. оси. В таком случае  . Необходимое для этого расстояние от источника до преломляющей поверхности будет равно
. Необходимое для этого расстояние от источника до преломляющей поверхности будет равно 
 Выполнив несложные преобразования, можно получить
Выполнив несложные преобразования, можно получить  , учитывая
, учитывая  и
и  , где
, где  и
и 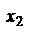 - расстояние от переднего фокуса до предмета и от заднего фокуса до изображения, тогда
- расстояние от переднего фокуса до предмета и от заднего фокуса до изображения, тогда  - формула Ньютона.
- формула Ньютона.  Увеличение. Уравнение Лагранжа-Гельмгольца. Выполним построение изображение небольших предметов при преломлении света на сферической поверхности. Свойства: а) луч, проходящий через оптический центр, не преломляется на сферической поверхности. б) луч, идущий через фокус, после преломления распространяется параллельно опт. оси. в) луч, падающий на сферическую поверхность, после преломления движется параллельно опт. оси. Рассм. сферическую поверхность с центром кривизны в точке О. Пусть точка А, расположенная на опт. оси, является предметом, А1 – ее изображение. Повернем прямую АА1 вокруг центра О на небольшой угол, так что точка А опишет небольшую дугу АВ а точка А1 – дугу А1В1. Так как для всех точек АВ и А1В1 соответствующие расстояния а1 и а2 одинаковы, то можно считать, что А1В1 является изображением дуги АВ. В виду того, что дуги АВ и А1В1 являются очень малыми, то их можно заменить соответствующими хордами. Точно также малая площадка, расположенная перпендикулярно опт. оси, в рассматриваемой сферической опт. системе отобразится при помощи параксиальных лучей в виде площадки, перпендикулярной опт. оси. П лоскость предмета АВ и плоскость его изображения А1В1 являются сопряженными плоскостями по отношению к данной опт. системе. Размер изображения может отличаться от исходного размера предмета. Отношение линейных размеров изображения А1В1 и предмета АВ называется поперечным, или линейным увеличением:
Увеличение. Уравнение Лагранжа-Гельмгольца. Выполним построение изображение небольших предметов при преломлении света на сферической поверхности. Свойства: а) луч, проходящий через оптический центр, не преломляется на сферической поверхности. б) луч, идущий через фокус, после преломления распространяется параллельно опт. оси. в) луч, падающий на сферическую поверхность, после преломления движется параллельно опт. оси. Рассм. сферическую поверхность с центром кривизны в точке О. Пусть точка А, расположенная на опт. оси, является предметом, А1 – ее изображение. Повернем прямую АА1 вокруг центра О на небольшой угол, так что точка А опишет небольшую дугу АВ а точка А1 – дугу А1В1. Так как для всех точек АВ и А1В1 соответствующие расстояния а1 и а2 одинаковы, то можно считать, что А1В1 является изображением дуги АВ. В виду того, что дуги АВ и А1В1 являются очень малыми, то их можно заменить соответствующими хордами. Точно также малая площадка, расположенная перпендикулярно опт. оси, в рассматриваемой сферической опт. системе отобразится при помощи параксиальных лучей в виде площадки, перпендикулярной опт. оси. П лоскость предмета АВ и плоскость его изображения А1В1 являются сопряженными плоскостями по отношению к данной опт. системе. Размер изображения может отличаться от исходного размера предмета. Отношение линейных размеров изображения А1В1 и предмета АВ называется поперечным, или линейным увеличением:  . Для перевернутого изображения y1 и y2 имеют различные знаки, поэтому величина
. Для перевернутого изображения y1 и y2 имеют различные знаки, поэтому величина  будет отрицательной. Из треугольников АВD и A1B1D имеем
будет отрицательной. Из треугольников АВD и A1B1D имеем  ,
,  , В параксиальном приближении
, В параксиальном приближении  , следовательно
, следовательно  , выражение показывает, что поскольку n1 и n2 всегда положительны, то знак увеличения Гл будет определяться отношением
, выражение показывает, что поскольку n1 и n2 всегда положительны, то знак увеличения Гл будет определяться отношением 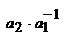 для действительных изображений это отношение будет отрицательным, для мнимых оно положительно. Кроме линейного увеличения опт. с-мы характеризуются угловым увеличением. Угловое увеличение
для действительных изображений это отношение будет отрицательным, для мнимых оно положительно. Кроме линейного увеличения опт. с-мы характеризуются угловым увеличением. Угловое увеличение  определяется как отношение тангенсов углов
определяется как отношение тангенсов углов  и
и  , которые составляют сопряженные лучи с опт. осью с-мы:
, которые составляют сопряженные лучи с опт. осью с-мы:  . Поскольку
. Поскольку  , получим:
, получим:  , это показывает, что угловое увеличение сферической поверхности прямо пропорционально отношению показателя преломления первой среды к показателю преломления второй и обратно пропорционально линейному увеличению. В случае, если все элементы опт. с-мы находятся в одной среде,
, это показывает, что угловое увеличение сферической поверхности прямо пропорционально отношению показателя преломления первой среды к показателю преломления второй и обратно пропорционально линейному увеличению. В случае, если все элементы опт. с-мы находятся в одной среде,  и
и  Для параксиальных лучей
Для параксиальных лучей  и
и 
 и
и 
 - уравнением Лагранжа-Гельмгольца. Уравнение Лагранжа-Гельмгольца справедливо для параксиальных лучей. В случае использования широких пучков условием получения стигматических изображений будет выполнение соотношения
- уравнением Лагранжа-Гельмгольца. Уравнение Лагранжа-Гельмгольца справедливо для параксиальных лучей. В случае использования широких пучков условием получения стигматических изображений будет выполнение соотношения  известного как условие синусов Аббе.
известного как условие синусов Аббе. 4.3.Основы матричного метода расчета центрированных опт. систем. Основной задачей геометрической оптики является построение стигматических изображений. т.к. каждая точка изобр. получается в результате схождения нескольких лучей, то решения обозначенной задачи важно уметь опр. ход лучей при их прохождении через опт. с-му. В большинстве случаев опт. с-ма представляет собой совокупность однородных сред, ограниченных плоскими или сферич. границами раздела, на которых происходит преломление, или отр. света. Траектория луча будет предст. Посл. прямых линий, находящихся в одной плоскости. Поэтому будем рассм. только меридиальные лучи, т.е. лучи, распростр. в одной плоскости (в плоскости YZ), проходящей через опт. ось с-мы, вдоль которой направлена ось Z. Для опр-ия хода лучей удобно воспользоваться корд. одной точки, принадл. лучу, и углом, который он составляет с некоторой осью, например, осью Z. Возьмем некоторую плоскость Z=const, перпендикулярную опт. оси и пересекающую рассматриваемый луч. Назовем ее опорной плоскостью ОП1. Любой меридиальный луч можно определить по отношению к опорной плоскости двумя параметрами: высотой y1, на которой рассматриваемы луч пересекает опорную плоскость, и углом u1, который он составляет с осью Z. Как и ранее будем пользоваться правилом знаков: координата y будет положительной, если точка пересечения находится выше оси Z, угол u1 будет положительным, если он соответствует вращению луча по часовой стрелке от положительного направления оси Z к направлению его распространения. Для определения координаты луча в некоторой новой точке необходимо снова провести опорную плоскость ОП2 и определить координаты y2 и u2. П ередаточная матрица. Рассм. вначале распространение света в однородной среде, в которой траектория луча представляет прямую линию. Проведем через точки А и В луча опорные плоскости, соответственно ОП1 и ОП2. Исходными координатами будем считать координаты y1 и u1. Определим координаты луча при его пересечении с опорной плоскостью ОП2, находящейся на расстоянии l от ОП1.
4.3.Основы матричного метода расчета центрированных опт. систем. Основной задачей геометрической оптики является построение стигматических изображений. т.к. каждая точка изобр. получается в результате схождения нескольких лучей, то решения обозначенной задачи важно уметь опр. ход лучей при их прохождении через опт. с-му. В большинстве случаев опт. с-ма представляет собой совокупность однородных сред, ограниченных плоскими или сферич. границами раздела, на которых происходит преломление, или отр. света. Траектория луча будет предст. Посл. прямых линий, находящихся в одной плоскости. Поэтому будем рассм. только меридиальные лучи, т.е. лучи, распростр. в одной плоскости (в плоскости YZ), проходящей через опт. ось с-мы, вдоль которой направлена ось Z. Для опр-ия хода лучей удобно воспользоваться корд. одной точки, принадл. лучу, и углом, который он составляет с некоторой осью, например, осью Z. Возьмем некоторую плоскость Z=const, перпендикулярную опт. оси и пересекающую рассматриваемый луч. Назовем ее опорной плоскостью ОП1. Любой меридиальный луч можно определить по отношению к опорной плоскости двумя параметрами: высотой y1, на которой рассматриваемы луч пересекает опорную плоскость, и углом u1, который он составляет с осью Z. Как и ранее будем пользоваться правилом знаков: координата y будет положительной, если точка пересечения находится выше оси Z, угол u1 будет положительным, если он соответствует вращению луча по часовой стрелке от положительного направления оси Z к направлению его распространения. Для определения координаты луча в некоторой новой точке необходимо снова провести опорную плоскость ОП2 и определить координаты y2 и u2. П ередаточная матрица. Рассм. вначале распространение света в однородной среде, в которой траектория луча представляет прямую линию. Проведем через точки А и В луча опорные плоскости, соответственно ОП1 и ОП2. Исходными координатами будем считать координаты y1 и u1. Определим координаты луча при его пересечении с опорной плоскостью ОП2, находящейся на расстоянии l от ОП1.  ,
,  . Будем рассматривать только лучи, составляющие малые углы с осью Z. В этом случае
. Будем рассматривать только лучи, составляющие малые углы с осью Z. В этом случае 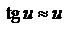 . Кроме того, в матричной оптике вместо углов используется величина
. Кроме того, в матричной оптике вместо углов используется величина 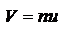 , называемая приведенным углом, т.е. можно переписать
, называемая приведенным углом, т.е. можно переписать  ,
,  , где
, где  ,
,  , величина L – приведенная длина. В матричной форме можно записать
, величина L – приведенная длина. В матричной форме можно записать  или
или 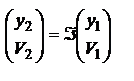 , где
, где  . Матрица Á называется передаточной
. Матрица Á называется передаточной матрицей или матрицей опт. промежутка. Отметим, что матрица Á является унимодулярной, т.е. ее определитель равен единице:
матрицей или матрицей опт. промежутка. Отметим, что матрица Á является унимодулярной, т.е. ее определитель равен единице: 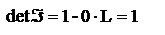 . Рассм. сферическую поверхность, которая разделяет две среды с показателями преломления n1 и n2, а так же имеет радиус кривизны R. Будем R считать положительным, если центр кривизны находится справа от границы раздела и отрицательным, если он находится слева. (Граница раздела сред принимается за начало оси Z). Проведем опорные плоскости 1 OП и 2 OП так, чтобы первая пересекла луч непосредственно перед точкой его падения на границу раздела, а вторая – непосредственно после его преломления. В параксиальном приближении расстояние между ОП1 и ОП2 будет очень малым и поэтому
. Рассм. сферическую поверхность, которая разделяет две среды с показателями преломления n1 и n2, а так же имеет радиус кривизны R. Будем R считать положительным, если центр кривизны находится справа от границы раздела и отрицательным, если он находится слева. (Граница раздела сред принимается за начало оси Z). Проведем опорные плоскости 1 OП и 2 OП так, чтобы первая пересекла луч непосредственно перед точкой его падения на границу раздела, а вторая – непосредственно после его преломления. В параксиальном приближении расстояние между ОП1 и ОП2 будет очень малым и поэтому  . Матрица преломления лучей на сферической поверхности. Запишем закон преломления луча на сферической поверхности:
. Матрица преломления лучей на сферической поверхности. Запишем закон преломления луча на сферической поверхности:  в параксиальном приближении
в параксиальном приближении  . Согласно теореме о внешнем угле треугольника
. Согласно теореме о внешнем угле треугольника  ,
,  . Умножим эти выражения соответственно на n1 и n2 и запишем с учетом закона преломления
. Умножим эти выражения соответственно на n1 и n2 и запишем с учетом закона преломления  . Откуда
. Откуда  ,
,  ,
,  , и в параксиальном приближении
, и в параксиальном приближении  , то
, то 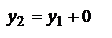 ,
,  . Величина
. Величина  является опт. силой преломляющей поверхности. В итоге запишем координаты луча при пересечении им ОП2:
является опт. силой преломляющей поверхности. В итоге запишем координаты луча при пересечении им ОП2:  ,
, 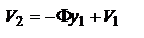 . Представим записанные равенства в матричном виде
. Представим записанные равенства в матричном виде  . Матрицу
. Матрицу  называют матрицей преломления. Заметим, что, как и в предыдущем случае, определитель матрицы
называют матрицей преломления. Заметим, что, как и в предыдущем случае, определитель матрицы  также равен единице:
также равен единице:  . Полученный результат может быть использован также для определения координат луча при его преломлении на плоской границе раздела двух сред. В случае плоской поверхности
. Полученный результат может быть использован также для определения координат луча при его преломлении на плоской границе раздела двух сред. В случае плоской поверхности 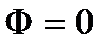 :
:  ,
,  . В итоге матрица преломления на плоской границе раздела параксиальном приближении будет иметь вид
. В итоге матрица преломления на плоской границе раздела параксиальном приближении будет иметь вид  . Центрированной системой называют совокупность опт. элементов, центры кривизны преломляющих и отражающих поверхностей которых расположены на одной прямой, которую называют гл. опт. осью с-мы. Основные элементы опт. с-мы: поверхности (сферические, плоские), которые служат границами раздела и могут быть преломляющими и отражающими; промежутки между ними. матричного метода для определения координат луча при его распространении через толстую линзу. В этом случае следует рассмотреть три опт. элемента: две преломляющие поверхности и промежуток между ними, равный толщине линзы l. Проведем четыре опорные плоскости: причем плоскость ОП1 проведем непосредственно перед передней преломляющей поверхностью. Опорную плоскость ОП2 проведем так, чтобы она пересекала параксиальный луч непосредственно сразу после преломления. Соответственно ОП3 будет проходить через точку падения параксиального луча на вторую преломляющую поверхность. И, наконец, опорную плоскость ОП4 проведем через вершину второй преломляющей поверхности. Именно по отношению к этой плоскости и будем определять координаты выходящего луча. Пусть
. Центрированной системой называют совокупность опт. элементов, центры кривизны преломляющих и отражающих поверхностей которых расположены на одной прямой, которую называют гл. опт. осью с-мы. Основные элементы опт. с-мы: поверхности (сферические, плоские), которые служат границами раздела и могут быть преломляющими и отражающими; промежутки между ними. матричного метода для определения координат луча при его распространении через толстую линзу. В этом случае следует рассмотреть три опт. элемента: две преломляющие поверхности и промежуток между ними, равный толщине линзы l. Проведем четыре опорные плоскости: причем плоскость ОП1 проведем непосредственно перед передней преломляющей поверхностью. Опорную плоскость ОП2 проведем так, чтобы она пересекала параксиальный луч непосредственно сразу после преломления. Соответственно ОП3 будет проходить через точку падения параксиального луча на вторую преломляющую поверхность. И, наконец, опорную плоскость ОП4 проведем через вершину второй преломляющей поверхности. Именно по отношению к этой плоскости и будем определять координаты выходящего луча. Пусть  - координаты луча падающего на ОП1,
- координаты луча падающего на ОП1, 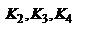 - координаты при пересечении соотв. оп. плоскостей. Пусть Á– матрица опт. промежутка, Â1и Â2- матрицы преломления на 1-й и 2-й сферической поверхности. Ф1 - оптическая сила 1-й поверхности, Ф2 - второй. Если радиусы кривизны поверхностей равны соответственно R1 и R2, то их оптическая сила будет равна
- координаты при пересечении соотв. оп. плоскостей. Пусть Á– матрица опт. промежутка, Â1и Â2- матрицы преломления на 1-й и 2-й сферической поверхности. Ф1 - оптическая сила 1-й поверхности, Ф2 - второй. Если радиусы кривизны поверхностей равны соответственно R1 и R2, то их оптическая сила будет равна  и
и  . Определим координаты выходящего луча
. Определим координаты выходящего луча  . Поскольку
. Поскольку  и
и  , то
, то  и
и  - матрица описывающая свойства с-мы. ТО, матрица сложной опт. с-мы равна произведению матриц ее отдельных элементов, записанных в обратном порядке. Можно записать
- матрица описывающая свойства с-мы. ТО, матрица сложной опт. с-мы равна произведению матриц ее отдельных элементов, записанных в обратном порядке. Можно записать  . Перемножив:
. Перемножив: 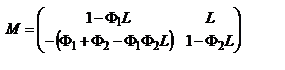 , величина
, величина  - опт. сила толстой линзы.
- опт. сила толстой линзы. 4.4. Кардинальные элементы центрированных опт. систем. Рассм. опт. с-му. Рассм. луч, падающий на опт. с-му параллельно ее опт. оси на некоторой высоте y1. В этом случае
4.4. Кардинальные элементы центрированных опт. систем. Рассм. опт. с-му. Рассм. луч, падающий на опт. с-му параллельно ее опт. оси на некоторой высоте y1. В этом случае 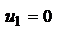 и
и 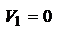 ; Параметры луча на выходе из с-мы, т.е. при его пересечении опорной плоскости ОП2:
; Параметры луча на выходе из с-мы, т.е. при его пересечении опорной плоскости ОП2:  ,
, 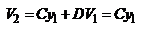 Пусть выходящий луч пересечет опт. ось в точке F2, которая расположена на расстоянии t2 от ОП2, причем
Пусть выходящий луч пересечет опт. ось в точке F2, которая расположена на расстоянии t2 от ОП2, причем  , где
, где  , тогда параметры можно переписать:
, тогда параметры можно переписать:  . Таким образом, t2 не зависит от y1. Это значит, что все параксиальные лучи, которые падают на опт. с-му параллельно ее гл. опт. оси, после прохождения через нее проходят через одну и ту же точку, лежащую на опт. оси, которую принято называть главным задним фокусом опт. с-мы. Если продолжить луч, который входит параллельно гл. опт. оси и луч, который выходит из опт. с-мы, то получим точку S2. Плоскость, проведенная через эту точку
. Таким образом, t2 не зависит от y1. Это значит, что все параксиальные лучи, которые падают на опт. с-му параллельно ее гл. опт. оси, после прохождения через нее проходят через одну и ту же точку, лежащую на опт. оси, которую принято называть главным задним фокусом опт. с-мы. Если продолжить луч, который входит параллельно гл. опт. оси и луч, который выходит из опт. с-мы, то получим точку S2. Плоскость, проведенная через эту точку  гл. опт. оси, называют гл. плоскостью. Точка H2 пересечения этой плоскости с гл. опт. осью наз-ся гл. точкой. Фокусным расстоянием опт. с-мы называется расстояние от гл. точки до фокуса, т.е. отрезок
гл. опт. оси, называют гл. плоскостью. Точка H2 пересечения этой плоскости с гл. опт. осью наз-ся гл. точкой. Фокусным расстоянием опт. с-мы называется расстояние от гл. точки до фокуса, т.е. отрезок 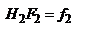
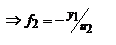 , после преобразований:
, после преобразований:  . Таким образом, фокусное расстояние опт. с-мы опр. элементом C матрицы M. опр-им расст. s2 от опорной пл-ти ОП2 до второй гл. пл-ти:
. Таким образом, фокусное расстояние опт. с-мы опр. элементом C матрицы M. опр-им расст. s2 от опорной пл-ти ОП2 до второй гл. пл-ти: 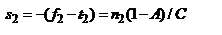 . Проведем луч F1E, под углом u1' к гл. опт. оси с таким расчетом, чтобы после прохождения через опт. с-му он был направлен параллельно гл. опт. оси. В этом случае
. Проведем луч F1E, под углом u1' к гл. опт. оси с таким расчетом, чтобы после прохождения через опт. с-му он был направлен параллельно гл. опт. оси. В этом случае  . Поскольку
. Поскольку 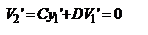 , то
, то 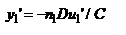 . Определим расстояние t1 от опорной плоскости ОП1 до точки пересечения данного луча с гл. опт. осью с-мы:
. Определим расстояние t1 от опорной плоскости ОП1 до точки пересечения данного луча с гл. опт. осью с-мы: 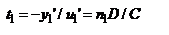 . Полученное соотн. показывает, что t1 не зависит от u1'. Это означает, что все лучи, исходящие из точки F1 после прохождения через опт. с-му будут также || ее гл. опт. оси. Продолжим падающий луч и вышедший до пересечения в точке S1. Плоскость, проходящая через эту точку
. Полученное соотн. показывает, что t1 не зависит от u1'. Это означает, что все лучи, исходящие из точки F1 после прохождения через опт. с-му будут также || ее гл. опт. оси. Продолжим падающий луч и вышедший до пересечения в точке S1. Плоскость, проходящая через эту точку  гл. опт. оси, н-ся гл. передней плоскостью. Соответственно точка пересечения этой пл-ти с опт-ой осью Н1 наз-ся гл. первой точкой опт-ой
гл. опт. оси, н-ся гл. передней плоскостью. Соответственно точка пересечения этой пл-ти с опт-ой осью Н1 наз-ся гл. первой точкой опт-ой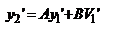 ,
,  . Из двух последних равенств:
. Из двух последних равенств:  . Учитывая (*):
. Учитывая (*):  . Откуда, учитывая свойства унимодулярности матрицы, при котором AD-DC=1, получим:
. Откуда, учитывая свойства унимодулярности матрицы, при котором AD-DC=1, получим:  . Расстояние s1 от опорной плоскости ОП1 до передней гл. точки Н1 будет равно:
. Расстояние s1 от опорной плоскости ОП1 до передней гл. точки Н1 будет равно:  . Еще 2 кардинальных элемента центр. опт. с-мы: узловые точки и узловые пл-ти. Узловые точки хар-ся св-м: всякий луч, входящий в опт. с-му под углом u1 и проходящий через узловую точку K1, выходит из опт. с-мы под тем же углом к опт. оси, пересекая ее во второй узловой точке K2. Пл-ти, проходящие через узловые точки перпенд. гл. опт. оси, наз-ся узловыми пл-ми. Обозначим через h1 расстояние от опорной плоскости ОП1 до точки K1 и соответств. расст. от опорной плоскости ОП2 до K2 - через – h2. Запишем матрицу
. Еще 2 кардинальных элемента центр. опт. с-мы: узловые точки и узловые пл-ти. Узловые точки хар-ся св-м: всякий луч, входящий в опт. с-му под углом u1 и проходящий через узловую точку K1, выходит из опт. с-мы под тем же углом к опт. оси, пересекая ее во второй узловой точке K2. Пл-ти, проходящие через узловые точки перпенд. гл. опт. оси, наз-ся узловыми пл-ми. Обозначим через h1 расстояние от опорной плоскости ОП1 до точки K1 и соответств. расст. от опорной плоскости ОП2 до K2 - через – h2. Запишем матрицу  преобразования лучей между узловыми плоскостями:
преобразования лучей между узловыми плоскостями:  , где
, где  ,
, 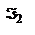 - передаточные матрицы смещения лучей между опорными и узловыми плоскостями:
- передаточные матрицы смещения лучей между опорными и узловыми плоскостями:  ,
,  . 1ое во 2ое, получим:
. 1ое во 2ое, получим: 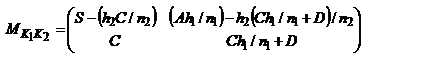 . можно упросить. Запишем координаты луча y2 и V2 при пересечении им второй узловой плоскости, считая заданными его координаты y1 и V1 при пересечении передней узловой плоскости:
. можно упросить. Запишем координаты луча y2 и V2 при пересечении им второй узловой плоскости, считая заданными его координаты y1 и V1 при пересечении передней узловой плоскости: 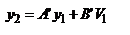 ,
, 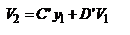 . Поскольку узловые точки расположены на гл. опт. оси, то
. Поскольку узловые точки расположены на гл. опт. оси, то  , соответственно
, соответственно  . Это возможно если
. Это возможно если 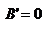 . Далее, на основании свойства узловых точек
. Далее, на основании свойства узловых точек 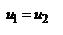 или
или  , можем записать (при
, можем записать (при  ):
):  Используя записанные условия, получим
Используя записанные условия, получим  и
и  , покажем, что расстояние между узлами всегда равно расстоянию между главными точками. Действительно, расстояние между узлами, расстояние К1К2 с учетом правила знаков будет равно:
, покажем, что расстояние между узлами всегда равно расстоянию между главными точками. Действительно, расстояние между узлами, расстояние К1К2 с учетом правила знаков будет равно:  . Или, принимая во внимание выражения для h1 и h2, запишем
. Или, принимая во внимание выражения для h1 и h2, запишем 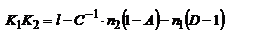 . Точно такой результат получается и для расстояния
. Точно такой результат получается и для расстояния  . В случае, если опт. св-ва среды по обе стороны с-мы одинаковы
. В случае, если опт. св-ва среды по обе стороны с-мы одинаковы  , то узловые точки совпадают с гл. Фокусное расст. опт. с-мы (опт. сила) определяются элементом С. Заметим, что при
, то узловые точки совпадают с гл. Фокусное расст. опт. с-мы (опт. сила) определяются элементом С. Заметим, что при  имеем:,
имеем:,  т.е. переднее фокусное расст. равно заднему фокусному расст. При
т.е. переднее фокусное расст. равно заднему фокусному расст. При  :
:  . Точки F1 и F2, H1 и H2, K1 и K2 а так же плоскости, которые проходят через них перпендикулярно гл. опт. оси, называются кардинальными. MН преобразования лучей между передней H1 и задней H2 гл. плоскостями:
. Точки F1 и F2, H1 и H2, K1 и K2 а так же плоскости, которые проходят через них перпендикулярно гл. опт. оси, называются кардинальными. MН преобразования лучей между передней H1 и задней H2 гл. плоскостями:  , где
, где  - матрица опт. промежутка от Н2 до ОП2 толщиной s2, M – матрица преобразования лучей между ОП2 ОП1,
- матрица опт. промежутка от Н2 до ОП2 толщиной s2, M – матрица преобразования лучей между ОП2 ОП1,  - матрица опт. промежутка от ОП1 до H2. Подставив всё в MH:
- матрица опт. промежутка от ОП1 до H2. Подставив всё в MH:  , перемножив и учитывая св-ва унимодулярности:
, перемножив и учитывая св-ва унимодулярности:  . Поскольку A=1, B=0, то
. Поскольку A=1, B=0, то 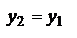 ,
,  сопряжённые точки, на гл. плоскостях отображаются с линейным увеличением, равным ед., т.е. любой луч, который проходит через плоскость H1, пересечет H2 на той же высоте. матрицу преобразования лучей между двумя фокальными плоскостями F1 и о F2:
сопряжённые точки, на гл. плоскостях отображаются с линейным увеличением, равным ед., т.е. любой луч, который проходит через плоскость H1, пересечет H2 на той же высоте. матрицу преобразования лучей между двумя фокальными плоскостями F1 и о F2:  , здесь
, здесь  ,
, 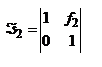 , перемножив:
, перемножив:  все
все
 4.5 Аберрации опт. Систем. Место схожд. стигматического пучка наз-ся фокусом. Его волновая пов-ть является сферической. Астигматическим называется пучок, не имеющий точки схождения. Поверхность астигматического пучка несферическая. Параксиальный пучок при прохождении через центрированную опт. с-му остается гомоцентрическим. Центрированная оптическая с-ма при использовании параксиальных лучей дает стигматическое изображение. Однако параксиальный пучок является идеализацией. В практической оптике используются широкие непараксиальные пучки, которые к тому же являются немонохром. Это приводит к тому, что получаемое изобр. уже не будет полностью геом. подобным предмету, т.е. будут возникать искажения изобр-ия. В таком случае говорят, что опт. с-ма обладает погрешностями, т.е. аберрациями. В общем случае: аберрация - любое нарушение гомоцентричности светового пучка вызванное его прохожд. через опт. с-му. Аберрации опт. с-м бывают монохром. и хроматические. Монохром.аберрации возникают при прохождении монохром. непараксиальных пучков через опт. с-му. Хроматические аберрации имеют место при использовании немонохром. пучков света. Вследствие явления дисперсии света коэфф. преломления, а, следовательно, и точка схождения лучей различной длины, будут различными. Это приводит к тому, что даже при отсутствии монохроматических аберрации, изображение, получаемое в белом свете, будет окрашенным. Процесс устранения аберраций опт. с-мы называется корригированием. Полностью устранить аберрации нельзя, но можно уменьшить до нужной величины. Например, при рассм. предмета визуально, или с помощью опт. прибора размер аберрации должен быть меньше min разрешаемого ими геом. размера. В этом случае аберрации не будут влиять на качество изобр. Рассм. монохром. аберрации. Одной из наиболее часто встречаемых аберраций является сферическая аберрация. возникает при отображении широким пучком точек, лежащих на опт. оси. рассм. точечный объект А, расположенный на опт. оси. Из всей совокупности лучей, падающих на линзу, выделим 2 пары: 1-1' и 2-2'. Для 1ой углы падения на преломляющую пов-ть являются малыми, и параксиальное приближение выполняется с большой точностью. Эти лучи образуют стигматическое изобр. в точке А1. Для второй пары лучей углы падения будут больше чем для параксиальных лучей, поэтому и углы преломл. также будут больше. Это приведет к тому, что они пересекут опт.ось в точке А2, расположенной ближе к линзе. Наблюдая изобр. на экране, заметим, что ни при каком его положении не получится точечное изобр. если расположить экран перпенд. опт. оси так, чтобы он проходил через точку А1, то изобр. будет иметь вид яркой точки в центре, окруженной светлым ореолом, к-ый наз-т кружком рассеяния. Центр изобр. будут создавать параксиальные лучи; кружок рассеяния будут создавать непаракс. лучи. Вблизи точки А1 имеется зона max концентрации световой энергии. Поверхность, огибающая эту область пространства, называется каустической поверхностью, или каустикой. В сечении каустика представляет геом. место точек схождения меридиональных лучей. Сферическая аберрация х-ся разностью коорд. точек A1 и A2: δs=OA1-OA2. Это разность называется продольной аберрацией. Продольная аберрация считается (+), если точка А2 расположена правее точки А1 и (-) – если точка А2 расположена левее А1. В приведенном на рис. примере продольная аберрация будет (-). Кроме величины δs продольная аберрация характеризуется величиной δs =CD - размером кружка рассеяния на экране, расположенном в плоскости параксиального изображения, вдоль направления перпенд. опт. оси. Собирающая линза имеет отрицательную аберрацию продольную аберрацию, рассеивающая – положительную. Размер продольной и поперечной аберрации зависит от апертуры пучка, падающего на линзу. Осуществляя диафрагмирование пучка, можно значительно уменьшить сферическую аберрацию. Однако, диафрагмирование приводит к уменьшению освещенности изображения. Кроме того, в случае микроскопа уменьшение апертуры нежелательно еще и потому, что это уменьшает их разрешающую способность. Сферическую аберрацию можно в значительной мере уменьшить, используя комбинацию из нескольких собирающих и рассеивающих линз. Аберрация кома. Часто источник, посылающий на линзу широкий пучок, расположен вне опт. оси. В этом случае каустика не имеет осевой симметрии. Она симм. отн-но меридиональной плоскости и по форме напоминает комету с хвостом. Такой вид погрешности опт. систем называется аберрацией кома. В отличие от сферической аберрации, кома определяется не только сферичностью поверхности линзы, но удаленностью от опт. оси с-мы. Действительно, при наклонном падении широкого пучка на линзу его верхние и нижние лучи преломляются по-разному. В итоге широкий параллельный пучок дает на экране не точечное изображение, а пятно довольно сложной формы. Кома является одной из наиболее существенных аберраций, особенно в микроскопии, где используют широкие пучки. Аберрация кома полностью устраняется при выполнении условия: y1n1sinu1= y2n2sinu2, где y1, y2 - размер предмета и изображения, u1, u2 - апертура лучей падающих на объектив и лучей, форм. изобр. это усл-ие синусов Аббе, может быть получено как следствие физического требования в соответствии, с которым для получения стигматического изобр. необходимо, чтобы опт. длина путей между сопряженными точками предмета и изображения были одинаковыми. Точки, для которых устранена сферическая аберрация и выполнено условие синусов Аббе, наз-ся апланатическими. Получаемые при этом изображения также называются апланатическими. Опт. с-ма может давать апланатическое изобр. только при опр. расст. до предмета и изобр.. Это усл-ие выполняется в микроскопе, где предмет всегда располагается в одной плоскости, находящейся вблизи фокальной плоскости. Причиной хроматической аберрации является явление дисперсии света в веществе, из которого изготовлена линза.
4.5 Аберрации опт. Систем. Место схожд. стигматического пучка наз-ся фокусом. Его волновая пов-ть является сферической. Астигматическим называется пучок, не имеющий точки схождения. Поверхность астигматического пучка несферическая. Параксиальный пучок при прохождении через центрированную опт. с-му остается гомоцентрическим. Центрированная оптическая с-ма при использовании параксиальных лучей дает стигматическое изображение. Однако параксиальный пучок является идеализацией. В практической оптике используются широкие непараксиальные пучки, которые к тому же являются немонохром. Это приводит к тому, что получаемое изобр. уже не будет полностью геом. подобным предмету, т.е. будут возникать искажения изобр-ия. В таком случае говорят, что опт. с-ма обладает погрешностями, т.е. аберрациями. В общем случае: аберрация - любое нарушение гомоцентричности светового пучка вызванное его прохожд. через опт. с-му. Аберрации опт. с-м бывают монохром. и хроматические. Монохром.аберрации возникают при прохождении монохром. непараксиальных пучков через опт. с-му. Хроматические аберрации имеют место при использовании немонохром. пучков света. Вследствие явления дисперсии света коэфф. преломления, а, следовательно, и точка схождения лучей различной длины, будут различными. Это приводит к тому, что даже при отсутствии монохроматических аберрации, изображение, получаемое в белом свете, будет окрашенным. Процесс устранения аберраций опт. с-мы называется корригированием. Полностью устранить аберрации нельзя, но можно уменьшить до нужной величины. Например, при рассм. предмета визуально, или с помощью опт. прибора размер аберрации должен быть меньше min разрешаемого ими геом. размера. В этом случае аберрации не будут влиять на качество изобр. Рассм. монохром. аберрации. Одной из наиболее часто встречаемых аберраций является сферическая аберрация. возникает при отображении широким пучком точек, лежащих на опт. оси. рассм. точечный объект А, расположенный на опт. оси. Из всей совокупности лучей, падающих на линзу, выделим 2 пары: 1-1' и 2-2'. Для 1ой углы падения на преломляющую пов-ть являются малыми, и параксиальное приближение выполняется с большой точностью. Эти лучи образуют стигматическое изобр. в точке А1. Для второй пары лучей углы падения будут больше чем для параксиальных лучей, поэтому и углы преломл. также будут больше. Это приведет к тому, что они пересекут опт.ось в точке А2, расположенной ближе к линзе. Наблюдая изобр. на экране, заметим, что ни при каком его положении не получится точечное изобр. если расположить экран перпенд. опт. оси так, чтобы он проходил через точку А1, то изобр. будет иметь вид яркой точки в центре, окруженной светлым ореолом, к-ый наз-т кружком рассеяния. Центр изобр. будут создавать параксиальные лучи; кружок рассеяния будут создавать непаракс. лучи. Вблизи точки А1 имеется зона max концентрации световой энергии. Поверхность, огибающая эту область пространства, называется каустической поверхностью, или каустикой. В сечении каустика представляет геом. место точек схождения меридиональных лучей. Сферическая аберрация х-ся разностью коорд. точек A1 и A2: δs=OA1-OA2. Это разность называется продольной аберрацией. Продольная аберрация считается (+), если точка А2 расположена правее точки А1 и (-) – если точка А2 расположена левее А1. В приведенном на рис. примере продольная аберрация будет (-). Кроме величины δs продольная аберрация характеризуется величиной δs =CD - размером кружка рассеяния на экране, расположенном в плоскости параксиального изображения, вдоль направления перпенд. опт. оси. Собирающая линза имеет отрицательную аберрацию продольную аберрацию, рассеивающая – положительную. Размер продольной и поперечной аберрации зависит от апертуры пучка, падающего на линзу. Осуществляя диафрагмирование пучка, можно значительно уменьшить сферическую аберрацию. Однако, диафрагмирование приводит к уменьшению освещенности изображения. Кроме того, в случае микроскопа уменьшение апертуры нежелательно еще и потому, что это уменьшает их разрешающую способность. Сферическую аберрацию можно в значительной мере уменьшить, используя комбинацию из нескольких собирающих и рассеивающих линз. Аберрация кома. Часто источник, посылающий на линзу широкий пучок, расположен вне опт. оси. В этом случае каустика не имеет осевой симметрии. Она симм. отн-но меридиональной плоскости и по форме напоминает комету с хвостом. Такой вид погрешности опт. систем называется аберрацией кома. В отличие от сферической аберрации, кома определяется не только сферичностью поверхности линзы, но удаленностью от опт. оси с-мы. Действительно, при наклонном падении широкого пучка на линзу его верхние и нижние лучи преломляются по-разному. В итоге широкий параллельный пучок дает на экране не точечное изображение, а пятно довольно сложной формы. Кома является одной из наиболее существенных аберраций, особенно в микроскопии, где используют широкие пучки. Аберрация кома полностью устраняется при выполнении условия: y1n1sinu1= y2n2sinu2, где y1, y2 - размер предмета и изображения, u1, u2 - апертура лучей падающих на объектив и лучей, форм. изобр. это усл-ие синусов Аббе, может быть получено как следствие физического требования в соответствии, с которым для получения стигматического изобр. необходимо, чтобы опт. длина путей между сопряженными точками предмета и изображения были одинаковыми. Точки, для которых устранена сферическая аберрация и выполнено условие синусов Аббе, наз-ся апланатическими. Получаемые при этом изображения также называются апланатическими. Опт. с-ма может давать апланатическое изобр. только при опр. расст. до предмета и изобр.. Это усл-ие выполняется в микроскопе, где предмет всегда располагается в одной плоскости, находящейся вблизи фокальной плоскости. Причиной хроматической аберрации является явление дисперсии света в веществе, из которого изготовлена линза.  Действительно, фокусное расстояние тонкой линзы определяется выражением
Действительно, фокусное расстояние тонкой линзы определяется выражением 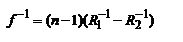
 Хроматическая аберрация. Ахроматизация линз., продифф.:
Хроматическая аберрация. Ахроматизация линз., продифф.:  или
или  , где
, где 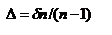 - отн-ая дисперсия. Если световой пучок, падающий на линзу, является немонохром., то при изменении длины волны величина
- отн-ая дисперсия. Если световой пучок, падающий на линзу, является немонохром., то при изменении длины волны величина  , т.е.
, т.е.  и фокусное расстояние для волн различной длины будет различным. Это приводит к тому, что положение изображения в немонохроматическом свете будет различным, т.е. к хроматической аберрации. Если используются две линзы, сложенные вплотную, то фокусное расстояние такой опт. с-мы будет равно
и фокусное расстояние для волн различной длины будет различным. Это приводит к тому, что положение изображения в немонохроматическом свете будет различным, т.е. к хроматической аберрации. Если используются две линзы, сложенные вплотную, то фокусное расстояние такой опт. с-мы будет равно  , продифференцировав:
, продифференцировав: 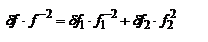 , решив:
, решив:  Для ахроматизации, т.е. исчезновения хроматической аберрации, необходимо выполнение условия
Для ахроматизации, т.е. исчезновения хроматической аберрации, необходимо выполнение условия  или
или  - Это усл-ие может быть выполнено, только если слагаемые имеют различные знаки. Поскольку
- Это усл-ие может быть выполнено, только если слагаемые имеют различные знаки. Поскольку  и
и 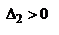 (линзы работают в области нормальной дисперсии), то для выполнения условия необходимо, чтобы различные знаки имели f1 и f2, т.е. одна линза должна быть собирающей, а другая - рассеивающей. Пусть f1>0, f2<0, Если ахроматический объектив должен обладать положительной опт. силой, т.е. быть собирающим, то необходимо, чтобы
(линзы работают в области нормальной дисперсии), то для выполнения условия необходимо, чтобы различные знаки имели f1 и f2, т.е. одна линза должна быть собирающей, а другая - рассеивающей. Пусть f1>0, f2<0, Если ахроматический объектив должен обладать положительной опт. силой, т.е. быть собирающим, то необходимо, чтобы  , и
, и  . ТО, ахроматической объектив можно изготовить из двух линз, сложенных вплотную: собирающей и рассеивающей, если он должен иметь (+) опт. силу, то первую линзу необходимо изготовить из материала, обладающего большей отн-ой дисперсией. Если фокусное расст. ахроматического объектива известно, то можно определить f1 и f2:
. ТО, ахроматической объектив можно изготовить из двух линз, сложенных вплотную: собирающей и рассеивающей, если он должен иметь (+) опт. силу, то первую линзу необходимо изготовить из материала, обладающего большей отн-ой дисперсией. Если фокусное расст. ахроматического объектива известно, то можно определить f1 и f2:  ,
,  . Значения f1 и f2 достигаются подбором радиусов кривизны сферических пов-тей линз
. Значения f1 и f2 достигаются подбором радиусов кривизны сферических пов-тей линз  . Опт. с-мы, у которых устранена хроматическая аберрация, наз-ся ахроматизироваными. Следует заметить, что полностью устранить хроматическую аберрацию невозможно. Обычно ее устраняют для какой-либо опр. спектральной обл. В приборах, предназначенных для визуальных наблюдений, это обычно желто-зеленая область. Хроматическая аберрация является крайне нежелательной в микроскопах. Поэтому их составные части являются ахроматизироваными. Объективы, у которых ахроматизация выполнена для двух цветов спектра называют ахроматами. Однако во многих случаях, которые имеют место в микроскопии, такой ахроматизации недостаточно. Аббе определил условия, при которых достигается ахроматизация объективов для трех длин волн. Такие объективы наз-ся апохроматами. Апохроматы широко используются в опт. микроскопах. Астигматизм наклонных пучков и кривизна поля. Даже узкие пучки утрачивают гомоцентричность при прохождении через опт. с-му, если они составляют с опт. осью значительные углы. Для того, чтобы наглядно представить характер искажений, возникающих в этом случае, введем несколько опр. Плоскость, проходящую через опт. ось с-мы и центральный луч падающего пучка, наз-ся меридианальной. Часто эта плоскость совмещается с плоскостью рисунка. Плоскость, перпенд. меридианальной плоскости и также содержащая центральный луч, наз-ся саггитальной. Рассм. гомоцентрический узкий пучок света, исходящий из точки А и падающий на опт. с-му под углом к ее гл. опт. оси. Пусть mm и ss – сечения линзы меридианальной и саггитальной плоскостью соответственно. Вследствие различия радиусов кривизны преломляющих пов-ей в этих взаимно перпенд. сечениях, волновая пов-ть пучка после преломления будет не сферической. Меридианальные лучи пересекаться на фокальной линии Рm, расположенной в саггитальной плоскости, саггитальные лучи на линии Рs, расположенной в меридианальной плоскости. Расстояние между этими линиями, которое мы опр-ли как астигматическая разность, быстро возрастает с увеличением угла между пучком и опт. осью. Такой вид аберрации наз-ся астигматизмом. Астигматизм приводит к искривлению поля изобр., т.е. изобр. даже плоской фигуры оказывается не совсем резким на плоскости. Астигматизм крайне нежелателен для фотообъективов, которые должны давать резкие изобр. на плоскости пленки и светочувствительной матрицы. Комбинируя линзы с различным радиусом кривизны пов-ти и фокусными расст., можно приблизительно совместить меридианальные и саггитальные фокальные линии, сделав их практически прямыми. Опт. с-мы, у которых исправлена аберрация астигматизма, называются анастигматами.
. Опт. с-мы, у которых устранена хроматическая аберрация, наз-ся ахроматизироваными. Следует заметить, что полностью устранить хроматическую аберрацию невозможно. Обычно ее устраняют для какой-либо опр. спектральной обл. В приборах, предназначенных для визуальных наблюдений, это обычно желто-зеленая область. Хроматическая аберрация является крайне нежелательной в микроскопах. Поэтому их составные части являются ахроматизироваными. Объективы, у которых ахроматизация выполнена для двух цветов спектра называют ахроматами. Однако во многих случаях, которые имеют место в микроскопии, такой ахроматизации недостаточно. Аббе определил условия, при которых достигается ахроматизация объективов для трех длин волн. Такие объективы наз-ся апохроматами. Апохроматы широко используются в опт. микроскопах. Астигматизм наклонных пучков и кривизна поля. Даже узкие пучки утрачивают гомоцентричность при прохождении через опт. с-му, если они составляют с опт. осью значительные углы. Для того, чтобы наглядно представить характер искажений, возникающих в этом случае, введем несколько опр. Плоскость, проходящую через опт. ось с-мы и центральный луч падающего пучка, наз-ся меридианальной. Часто эта плоскость совмещается с плоскостью рисунка. Плоскость, перпенд. меридианальной плоскости и также содержащая центральный луч, наз-ся саггитальной. Рассм. гомоцентрический узкий пучок света, исходящий из точки А и падающий на опт. с-му под углом к ее гл. опт. оси. Пусть mm и ss – сечения линзы меридианальной и саггитальной плоскостью соответственно. Вследствие различия радиусов кривизны преломляющих пов-ей в этих взаимно перпенд. сечениях, волновая пов-ть пучка после преломления будет не сферической. Меридианальные лучи пересекаться на фокальной линии Рm, расположенной в саггитальной плоскости, саггитальные лучи на линии Рs, расположенной в меридианальной плоскости. Расстояние между этими линиями, которое мы опр-ли как астигматическая разность, быстро возрастает с увеличением угла между пучком и опт. осью. Такой вид аберрации наз-ся астигматизмом. Астигматизм приводит к искривлению поля изобр., т.е. изобр. даже плоской фигуры оказывается не совсем резким на плоскости. Астигматизм крайне нежелателен для фотообъективов, которые должны давать резкие изобр. на плоскости пленки и светочувствительной матрицы. Комбинируя линзы с различным радиусом кривизны пов-ти и фокусными расст., можно приблизительно совместить меридианальные и саггитальные фокальные линии, сделав их практически прямыми. Опт. с-мы, у которых исправлена аберрация астигматизма, называются анастигматами. Колбочек существует три типа отличающихся фоточувствительным пигментом. Колбочки обычно называют "синими", "зелеными" и "красными" в соответствии с наименованием цвета, для которого они оптимально чувствительны. Упомянутые три пигмента имеют максимальные поглощения приблизительно на 430, 530 и 560 нм. Этим длинам волн соответствует фиолетовый, сине-зеленый и желто-зеленый. Бинокулярное зрение: вырабатывавшаяся тысячелетиями, согласованная работа глаз постепенно создала новое чувство или ощущение глубины или рельефа, обусловливаемое двумя обстоятельствами: 1) непараллельностью (конвергенцией) оптических осей, направленных на наблюдаемый предмет 2) неодинаковостью изображений, получаемых на обеих сетчатках. Лупа: Лупа - простейшая оптическая система с фокусным расстоянием 100¸10 мм.
Колбочек существует три типа отличающихся фоточувствительным пигментом. Колбочки обычно называют "синими", "зелеными" и "красными" в соответствии с наименованием цвета, для которого они оптимально чувствительны. Упомянутые три пигмента имеют максимальные поглощения приблизительно на 430, 530 и 560 нм. Этим длинам волн соответствует фиолетовый, сине-зеленый и желто-зеленый. Бинокулярное зрение: вырабатывавшаяся тысячелетиями, согласованная работа глаз постепенно создала новое чувство или ощущение глубины или рельефа, обусловливаемое двумя обстоятельствами: 1) непараллельностью (конвергенцией) оптических осей, направленных на наблюдаемый предмет 2) неодинаковостью изображений, получаемых на обеих сетчатках. Лупа: Лупа - простейшая оптическая система с фокусным расстоянием 100¸10 мм.  , где
, где  - фокусное расстояние лупы.
- фокусное расстояние лупы. К расчету увеличения лупы. Микроскоп: Первый микроскоп был построен голландским мастером Янсеном. Первое удачное применение микроскопа в научных исследованиях связано с именем английского ученого Гука (1665 г.), котор
К расчету увеличения лупы. Микроскоп: Первый микроскоп был построен голландским мастером Янсеном. Первое удачное применение микроскопа в научных исследованиях связано с именем английского ученого Гука (1665 г.), котор 


