
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы проецирования земной поверхностиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Для составления топографических карт и планов точки земной поверхности проецируют на поверхность референц-эллипсоида или на плоскость. Проецирование на поверхность референц-эллипсоида выполняется вдоль отвесных линий. Четырехугольник аbcd, полученный проецированием на сферическую поверхность эллипсоида, называют горизонтальной проекцией четырехугольника ABCD местности (рис. 2.4).
При проецировании небольших по площади участков местности, основную уровенную поверхность можно принимать за плоскость. В таком случае отвесные линии можно считать параллельными между собой и горизонтальная проекция практически преобразуется в ортогональную. Согласно рис. 2.5 отрезки ab, bc, cd,… являются ортогональными проекциями соответствующих линий AB, BC, CD,…, углы abc, bcd,… – ортогональными проекциями соответствующих углов ABC, BCD,…, а плоский многоугольник abcd – ортогональной проекцией пространственного многоугольника ABCD. Положение точек и линий местности АВ,ВС,… в ортогональной проекции определяется длинами горизонтальных проложений ab,bc,… и горизонтальными углами между ними. Длина ортогональной проекции линии местности MN на горизон-тальную плоскость p называется горизонтальным проложением S этой линии (рис. 2.6) и вычисляется из прямоугольного треугольника MNC по формуле S = L×cos ν. Угол ν между линией местности MN и ее ортогональной проекцией на горизонтальную плоскость S = mn,измеряют непосредственно и называют углом наклона линии. Ортогональные проекции линий на плоскость при ν ≠ 0 всегда меньше соответствующих им отрезков на физической поверхности Земли. Размеры участков земной поверхности, Принимаемые за плоскость
Определим разность между длиной касательной S и длиной дуги S1. Выразим угол a в радианах, тогда согласно рис. 2.7 получим, что S = R × tga, а S1 = R×a. Откуда следует, что D S = R(tga -a). (2.1) Центральный угол a по своей величине незначителен. Поэтому при разложении tga в убывающий ряд можно ограничиться вторым членом ряда и пренебречь последующими из-за их незначительности. Тогда
Из формулы S1=R×a получим, что
Из рис. 2.7 видно, что точка D находится на уровенной поверхности и ее высота равна нулю. Определим величину отрезка, характеризующего отклонение точки Q от уровенной поверхности. Для этого рассмотрим прямоугольный треугольник OCQ, откуда (R + D h) ² = S ² + R ². Упростив данное равенство, имеем
Сравнивая формулы 2.3 и 2.4 видно, что значение D h существенно больше D S. Если условно принять радиус Земли постоянным, то можно вычислить расхождения D S между длинами дуг на уровенной поверхности и их проекциями на плоскость, а также отклонения высот точек D h от их положения на поверхности сферы из-за кривизны Земли (табл. 2.2). Таблица 2.2
Значение величины D S возрастает незначительно. При дуге 11 км D S составляет лишь 1:1 000 000 ее длины. Относительная погрешность измерения расстояний современными приборами составляет порядка 1:1 000 000. Поэтому принято считать, что участок радиусом 11 км можно принимать за плоскость, а при определении превышений между точками местности необходимо вводить поправку D h.
2.5. Cистемы координат, применяемые в топографии
Координаты – это величины, определяющие положение любой точки на поверхности или в пространстве в принятой системе координат. Система координат устанавливает начальные (исходные) точки, линии или плоскости для отсчета необходимых величин – начало отсчета координат и единицы их исчисления. В топографии и геодезии наибольшее применение получили системы географических, прямоугольных, полярных и биполярных координат.
Географические координаты – это угловые величины: долгота l и широта j. Географической долготой l называется двугранный угол, заключенный между плоскостью данного меридиана (проходящего через точку В) и плоскостью начального меридиана. За начальный (нулевой) меридиан принят меридиан, проходящий через центр главного зала Гринвичской обсерватории в пределах г. Лондона. Для точки В долгота определяется углом l = WCD. Счет долгот ведут от начального меридиана в обе стороны – на восток и на запад. В связи с этим различают западные и восточные долготы, которые изменяются от 0° до 180°. Географической широтой j называется угол, составленный плоскостью экватора и отвесной линией, проходящей через данную точку. Если Землю принимать за шар, то для точки В (рис. 2.8) широта j определяется углом DCB. Широты, отсчитываемые от экватора к северу, называются северными, а к югу – южными, они изменяются от 0° на экваторе до 90° на полюсах. Географические координаты могут быть получены на основании астрономических наблюдений или геодезических измерений. В первом случае их называют астрономическими, а во втором – геодезическими (L – долгота, B – широта). При астрономических наблюдениях проецирование точек на поверхность относимости осуществляется отвесными линиями, при геодезических измерениях – нормалями. Поэтому величины астрономических и геодезических координат отличаются на величину уклонения отвесной линии. Использование разными государствами различных референц-эллипсоидов приводит к различиям координат одних и тех же пунктов, вычисленных относительно разных исходных поверхностей. Практически это выражается в общем смещении картографического изображения относительно меридианов и параллелей на картах крупного и среднего масштабов.
называются линейные величины – абсцисса и ордината, определяющие положение точки на плоскости относительно исходных направлений.
Прямая ХХ (ось абсцисс) совмещается с направлением меридиана, проходящего через начало координат, или с направлением, параллельным некоторому меридиану. Прямая YY (ось ординат) проходит через точку О перпендикулярную оси абсцисс. В такой системе положение точки на плоскости определяется кратчайшим расстоянием до нее от осей координат. Положение точки А определяется длиной перпендикуляров Xа и Yа. Отрезок Xа называется абсциссой точки А, а Yа – ординатой этой точки. Прямоугольные координаты обычно выражаются в метрах. Осями абсцисс и ординат участок местности в точке О делится на четыре четверти (рис. 2.9). Название четвертей определяется принятыми обозначениями стран света. Четверти нумеруются по направлению хода часовой стрелки: I – СВ; II – ЮВ; III – ЮЗ; IV – СЗ. В табл. 2.3 показаны знаки абсцисс Х и ординат Y для точек, находящихся в разных четвертях и даны их названия. Таблица 2.3
Абсциссы точек, расположенные вверх от начала координат считаются положительными, а вниз от нее – отрицательными, ординаты точек, расположенные вправо – положительными, влево – отрицательными. Система плоских прямоугольных координат применяется на ограниченных участках земной поверхности, которые могут быть приняты за плоские.
Система биполярных координат (рис. 2.11) представляет собой два выбранных неподвижных полюса О1 и О2, соединенные прямой – полярной осью. Данная система координат позволяет определить положение точки М относительно полярной оси на плоскости при помощи двух углов b1 и b2, двух радиусов-векторов r 1 и r 2 или их комбинаций. Если известны прямоугольные координаты точек О1 и О2, то положение точки М можно вычислить аналитическим способом (см. 7.4).
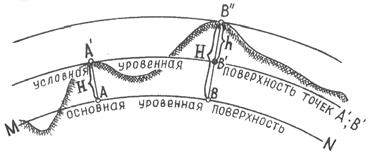
. Высоты точек земной поверхности. Для определения положения точек физической поверхности Земли недостаточно знать только плановые координаты X, Y или l, j, необходима третья координата – высота точки Н. Высотой точки Н (рис. 2.12) называется расстояние по отвесному направлению от данной точки (А ´; В ´´) до принятой основной уровенной поверхности MN. Числовое значение высоты точки называется отметкой. Высоты, отсчитываемые от основной уровенной поверхности MN, называют абсолютными высотами (АА ´; ВВ´´), а определяемые относительно произвольно выбранной уровенной поверхности – условными высотами (В´В´´). Разность высот двух точек или расстояние по отвесному направлению между уровенными поверхностями, проходящими через две любые точки Земли называется относительной высотой (В´В´´) или превышением этих точек h. В России, Украине, Беларуссии принята Балтийская система высот 1977 г. Счет высот ведется от уровенной поверхности, совпадающей со средним уровнем воды в Финском заливе, от нуля Кронштадского футштока.
2.6. Ориентирование направлений в топографии
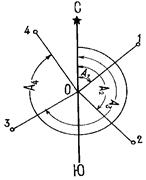
Ориентировать линию местности – значит определить ее направление относительно другого направления принятого за исходное. В топографии и геодезии исходными направлениями для ориентирования приняты географический меридиан, магнитный меридиан и осевой меридиан геодезической зоны, которые на топографических картах соответственно обозначаются: – линией со звездочкой (ê); – линией со стрелкой () и линией с угольником на конце (U). Направление географического меридиана получают из астрономических наблюдений, а направление магнитного меридиана определяет свободно подвешенная и уравновешенная магнитная стрелка. Магнитная ось стрелки в каждой точке земной поверхности совпадает с направлением магнитного меридиана этой точки. Географическим азимутом А направления, называется горизонтальный угол А, измеренный по ходу часовой стрелки от северного направления географического меридиана, проходящего через данную точку до ориентируемой линии (рис. 2.13). По абсолютному значению азимуты изменяются от 0 до 360°. На рисунке горизонтальные углы А 1, А 2, А 3, А 4 будут географическими азимутами ориентируемых направлений О1; О2; О3; О4. Точка О – начало ориентируемых направлений; а линия СЮ – географический меридиан точки О.
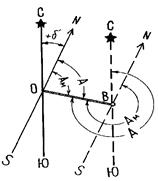
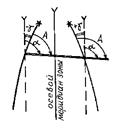
Магнитным азимутом направления называется горизонтальный угол А м между северным направлением магнитного меридиана и направлением данной линии, отсчитываемый по ходу часовой стрелки (рис. 2.14). Вследствие не совпадения географических и магнитных полюсов магнитный и географический меридианы в данной точке земной поверхности образуют между собой угол d, называемый склонением магнитной стрелки (рис. 2.14). Магнитное склонение может быть восточным – положительным, если северное направление магнитного меридиана находится к востоку от географического и западным – отрицательным, если северное направление магнитного меридиана проходит к западу от географического. Зависимость между географическим и магнитным азимутами выражается формулой А = А м + d. Склонение магнитной стрелки изменяется в зависимости от места и времени. Различают: суточные, годовые и вековые изменения склонения. Кроме того, величина склонения изменяется под влиянием магнитных бурь, связанных с полярным сиянием, солнечной активности, землетрясений, в районах магнитных аномалий и т. д. Суточные колебания склонения магнитной стрелки не превышают 5–15¢. Вследствие этого, ориентирование по магнитному азимуту проводится лишь в тех случаях, когда не требуется большая точность. В топографии и геодезии применяется также ориентирование направлений относительно северного направления оси абсцисс в системе прямоугольных координат. Угол, отсчитываемый от северного направления оси абсцисс или линии параллельной ему до данного направления, по ходу часовой стрелки называется дирекционным углом a (рис. 2.15). Дирекционный угол изменяется от 00 до 3600.
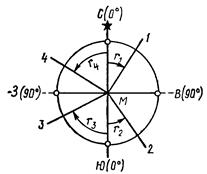
Угол между географическим меридианом данной точки и северным направлением оси абсцисс (вертикальной линией координатной сетки) называется сближением меридианов g (рис. 2.15). Сближение меридианов бывает восточным со знаком плюс и западным со знаком минус. При восточном сближении меридианов, линии параллельные осевому меридиану отклоняются к востоку от географического меридиана, проходящего через эту точку, а при западном – к западу. Зависимость между географическим азимутом и дирекционным углом выражается формулой А = a + g. Для того чтобы перейти от дирекционного угла к магнитному азимуту необходимо знать две величины – склонение магнитной стрелки и сближение меридианов. Данные об этих величинах в виде графика и текста помещаются под южной рамкой топографической карты. Магнитный азимут равен разности дирекционного угла и поправки направления А м = a – П. Поправка направления П – это угол между магнитным меридианом и северным направлением оси абсцисс. Поправка вычисляется по формуле Иногда ориентирование линии выражается острыми углами – румбами r. Румбом называют острый угол, отсчитываемый от ближайшего направления меридиана (северного или южного) до данной линии (рис. 2.16). Румбы имеют значения от 0° до 90° и сопровождаются названием четверти в которой проходит линия. Румбы переводят в азимуты и дирекционные углы и наоборот (табл. 2.4). Таблица 2.4
Зависимость между азимутами или дирекционными углами и румбами линий, расположенных в разных четвертях, устанавливают по формулам.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1400; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.57 (0.009 с.) |

 Рис. 2.4
Рис. 2.4
 Рис. 2.5
Рис. 2.5
 Рис. 2.6
Рис. 2.6
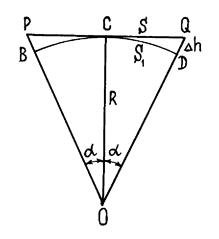 Рассмотрим, для каких по размерам участков местности можно применять ортогональное проецирование, т. е. при которых кривизна Земли может не учитываться в процессе создания карты или плана. На рис. 2.7 изображена часть поверхности Земли в виде дуги BCD радиуса R и ее проекция PQ на плоскость PCQ, где PC = CQ.
Рассмотрим, для каких по размерам участков местности можно применять ортогональное проецирование, т. е. при которых кривизна Земли может не учитываться в процессе создания карты или плана. На рис. 2.7 изображена часть поверхности Земли в виде дуги BCD радиуса R и ее проекция PQ на плоскость PCQ, где PC = CQ. . Подставим это значение в формулу 2.1. В результате получим, что
. Подставим это значение в формулу 2.1. В результате получим, что . (2.2)
. (2.2)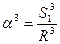 и заменим a в формуле 2.2. Окончательно найдем, что
и заменим a в формуле 2.2. Окончательно найдем, что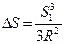 . (2.3)
. (2.3)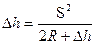 . Ввиду малого значения D h в сравнении с 2R окончательно получим, что
. Ввиду малого значения D h в сравнении с 2R окончательно получим, что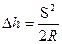 . (2.4)
. (2.4) Географические координаты (рис.
Географические координаты (рис. 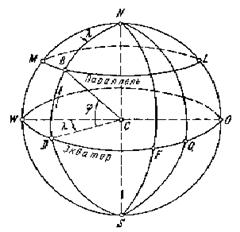 2.8) применяются для определения положения точек поверхности Земли на эллипсоиде (шаре). В этой системе координат исходными являются плоскость начального меридиана и плоскость экватора. Меридианом называют линию сечения эллипсоида плоскостью, проходящей через данную точку и ось вращения Земли. Параллелью называют линию сечения эллипсоида плоскостью, проходящей через данную точку и перпендикулярную земной оси. Параллель, плоскость которой проходит через центр эллипсоида, называется экватором. Через каждую точку, лежащую на поверхности земного шара, можно провести только один меридиан и только одну параллель.
2.8) применяются для определения положения точек поверхности Земли на эллипсоиде (шаре). В этой системе координат исходными являются плоскость начального меридиана и плоскость экватора. Меридианом называют линию сечения эллипсоида плоскостью, проходящей через данную точку и ось вращения Земли. Параллелью называют линию сечения эллипсоида плоскостью, проходящей через данную точку и перпендикулярную земной оси. Параллель, плоскость которой проходит через центр эллипсоида, называется экватором. Через каждую точку, лежащую на поверхности земного шара, можно провести только один меридиан и только одну параллель. Прямоугольными координатами (рис. 2.9)
Прямоугольными координатами (рис. 2.9)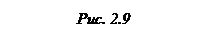 В геодезии и топографии принята правая система прямоугольных координат. Это отличает ее от левой системы координат, используемой в математике. Исходными направлениями служат две взаимно перпендикулярные линии с началом отсчета в точке их пересечения О.
В геодезии и топографии принята правая система прямоугольных координат. Это отличает ее от левой системы координат, используемой в математике. Исходными направлениями служат две взаимно перпендикулярные линии с началом отсчета в точке их пересечения О.
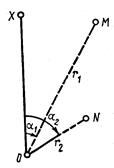 Координаты, началом отсчета которых является какая-либо точка местности, называются полярными. В данной системе координат производится измерение углов ориентирования. На горизонтальной плоскости (рис. 2.10) через произвольно выбранную точку О, называемую полюсом, проводят прямую ОХ – полярную ось. Тогда положение любой точки, например, М будет определяться радиусом – вектором r 1 и углом направления a1, а точки N – соответственно r 2 и a2. Углы a1 и a2 измеряют от полярной оси по ходу часовой стрелки до радиуса-вектора. Полярная ось может располагаться произвольно или совмещаться с направлением какого-либо меридиана, проходящего через полюс О.
Координаты, началом отсчета которых является какая-либо точка местности, называются полярными. В данной системе координат производится измерение углов ориентирования. На горизонтальной плоскости (рис. 2.10) через произвольно выбранную точку О, называемую полюсом, проводят прямую ОХ – полярную ось. Тогда положение любой точки, например, М будет определяться радиусом – вектором r 1 и углом направления a1, а точки N – соответственно r 2 и a2. Углы a1 и a2 измеряют от полярной оси по ходу часовой стрелки до радиуса-вектора. Полярная ось может располагаться произвольно или совмещаться с направлением какого-либо меридиана, проходящего через полюс О.
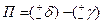 .
.


