
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Единицы мер в топографии и геодезииСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Совокупность единиц физических величин, принятых в государстве для измерений называется системой мер. При производстве геодезических измерений единицей угла служит градус, равный 1/360 части окружности или 1/90 части прямого угла (1º = 60΄, 1΄= 60΄΄). Пример: 11º 07´ 56´´. Наряду с градусной системой мер в некоторых странах употребляется десятичная или децимальная система, в которой прямой угол делят на 100 частей, называемых градами. Град делится на 100 минут или сантиград, а минута – на 100 секунд. Пример: 46g 68s 98ss или 46,6898 g. Значение угла может быть выражено в радианной мере. Радиан ρ – центральный угол, соответствующий длине дуге окружности, равной ее радиусу. Величина радиана – ρ = 57º 17΄ 44,8΄΄ или ρ° ≈ 57,3; ρ΄ ≈ 3438; ρ΄΄ ≈ 206 265, где ρ°, ρ΄, ρ΄΄ – число градусов, минут, секунд в радиане. Единица длины – метр (м). За метр принята длина “архивного метра” платинового жезла, хранящегося в международном бюро мер и весов во Франции. Длина жезла была принята равной одной десятимиллионной части четверти Парижского меридиана. В 1889 г. была изготовлена 31 копия «архивного метра», две из которых были переданы в Россию. Для создания надежно воспроизводимого эталона метра в 1960 г. было решено выражать его через длину световых волн. В 1983 г. принято новое определение метра, согласно которому метр равен расстоянию, проходящему в вакууме плоской электромагнитной волной за 1/299 792 458 доли секунды. Кратные единицы метра –1 км = 1000 м; 1 дм = 0,1 м; 1 см = 0,01 м и 1мм = 0,001 м. Единица площади – квадратный метр (м2). Кратные единицы – 1км2 = 1 000 000 м2 ; 1 см2 = 0,0001 м2 ; 10 000 м2 = 1 га; 1 км2 = 100 га. Единица времени – секунда (s). Секунда равна 9 192 631 770 периодам излучения, соответствующего перехода между двумя сверхтонкими уровнями основного состояния атома Цезия-133. 1m(мин) = 60s; 1h (час) = 3600 s. Единица температуры – градус по шкале Цельсия (°С). Единицей массы служит килограмм (кг).Копия представляет платиново-иридиевую гирю – цилиндр диаметром и высотой 39 мм. Единица силы – ньютон (Н). 1Н равен силе, сообщающей телу массой 1кг ускорение 1 м/сек2в направлении действия силы. Единицей измерения давления служит паскаль (Па).Паскаль равен давлению, вызываемому силой 1Н равномерно распределенной по нормальной к ней поверхности площадью 1м2. 1 Па= 9,87 × 10 –6 атм. или 7,60 × 10–3 мм.рт.ст. Давление, равное 1013 г Па на уровне моря на широте 45° принято считать нормальным. ОБЩИЕ СВЕДЕНИЯ
Форма и размеры Земли Физическая поверхность Земли представляет собой сочетание бесконечно большого числа неровностей. Она состоит из океанов, морей и материков с островами. Поверхность океанов в их спокойном состоянии ровная, а суша, составляющая только 29 % от общей площади Земли, представляет собой сложные сочетания гор, возвышенностей, равнин и низменностей. Поэтому поверхность Земли не имеет математического выражения, хотя для решения задач науки и практики требуется знать пространственное положение ее точек. Устанавливать их удобно относительно вспомогательной поверхности, близкой к реальной (физической) поверхности Земли. Такую поверхность называют поверхностью относимости, за которую принимается основная уровенная поверхность Земли, в каждой точке которой нормаль совпадает с направлением отвесной линии (с направлением силы тяжести). Это поверхность воды океанов и открытых морей, находящаяся в спокойном состоянии и мысленно продолженная под материками так, что к ней отвесные линии перпендикулярны во всех точках на Земле. Выбор поверхности воды океанов и морей за уровенную поверхность Земли, объясняется тем, что поверхность открытых водных пространств занимает 71 % общей площади Земли. В 1873 г. немецкий физик И. Б. Листинг назвал эту поверхность поверхностью геоида. Однако и фигура геоида сложна и строго неопределима, поскольку зависит от малоизученного распределения масс внутри Земли. Поэтому поверхность геоида не соответствует поверхности ни одной правильной математической фигуры, что не позволяет проводить расчеты, связанные с обработкой геодезических измерений на земной поверхности. По предложению ученого М. С. Молоденского вместо геоида в качестве промежуточной поверхности относимости используется квазигеоид, выполняющий роль «уровня моря». Положение его поверхности рассчитывается на основе гравиметрических измерений (см. 2.2). Поверхности квазигеоида и геоида совпадают с поверхностью Мирового океана и различаются по высоте на суше не более чем на 2,5 м. Геоид и квазигеоид по форме близко подходят к правильной математической фигуре – эллипсоиду вращения. Поэтому в качестве основной уровенной поверхности при обработке геодезических измерений, выполняемых на земной поверхности принята поверхность эллипсоида вращения, представляющего собой фигуру, полученную в результате вращения эллипса вокруг его малой оси (земной) эллипсоид. Угол между отвесной линией pq к поверхности геоида в данной точке и нормалью mn к поверхности эллипсоида называется уклонением отвесной линии e (рис. 2.1). В среднем, значение e составляет 3–4″, а в местах аномалий достигает десятков секунд.
Рис. 2.1
Земной эллипсоид характеризуется следующими основными элементами (рис. 2.2.): малой полуосью (полярный радиус)
На территории СССР пользовались эллипсоидом Ф. В. Бесселя до 1946 г. Однако этот эллипсоид был рассчитан в основном по данным Западной Европы. На Дальнем Востоке его поверхность сильно уклонялась от поверхности Земли. Более точные результаты размеров земного эллипсоида были получены в 1940 г.Ф. Н. Красовским и А. А. Изотовым по результатам астрономо-геодезических работ, выполненных на территории СССР, Западной Европы и США. Размеры земного эллипсоида, получившего название «референц-эллипсоида Красовского», были приняты для геодезических и картографических работ на всей территории СССР. Отклонения поверхности референц-эллипсоида Красовского от поверхности геоида не превышают 150 м. Точкой ориентирования референц-эллипсоида Красовского является центр круглого зала Пулковской обсерватории, широта В0 и долгота L0 которого определены из астрономических наблюдений и приняты исходными, а поверхность эллипсоида совмещена со средним уровнем воды в Финском заливе и отмечена на Кронштадском футштоке. В настоящее время основные геометрические параметры общеземного эллипсоида определяются более точными методами с использованием искусственных спутников Земли. Для сравнения в табл. 2.1 приведены размеры земного эллипсоида, определенные Бесселем, Красовским и в глобальной геоцентрической системе координат WGS – 84 (World Geodetic System 1984). Таблица 2.1. Размеры земного эллипсоида
При картографических работах (составление карт мелких масштабов) Землю достаточно принимать за шар, объем которого равен объему земного сфероида. Исходя из размеров эллипсоида Красовского R = 6 371 110 м.
2.2. Методы определения формы и размеров Земли Астрономо-геодезический метод. Определение формы и размеров Земли при помощи этого метода основано на использовании градусных измерений, суть которых сводится к определению линейной величины дуг меридианов и параллелей на разных широтах. Первое известное в истории определение длины земного меридиана, выполненное в античное время в Египте принадлежит Эратосфену. По его определениям длина меридианной окружности, равнялась 39 500 км, то есть очень близко к действительной величине меридиана 40 009 км. Ряд допущений, сделанных Эратосфеном, и несовершенный метод линейных измерений (расстояние определялось по длине караванного пути, измеренное в египетских стадиях (1 стадия может быть приравнена к 157,5 м) привели к приближенным результатам. Однако значение выполненных работ заключается в том, что Эратосфен впервые применил геодезический метод определения размеров Земли и получил довольно удовлетворительные для того времени результаты. Высокая точность измерения значительных по протяженности расстояний обеспечивается методом триангуляции, который был разработан в 1615 г. голландским ученым В. Снеллиусом. Триангуляция (от лат. triangulum – треугольник) – способ определения положения опорных геодезических пунктов А, В, С,… на местности путем построения сети примыкающих друг к другу треугольников, в которых измеряются все углы, а с помощью базиса аb определяется длина выходной стороны АВ в их ряду, длины же других сторон вычисляют по координатам этих пунктов (рис. 2.3).
Рис. 2.3
Триангуляция являлась основным способом создания опорной геодезической сети и градусных измерений до развития и становления космического метода. Триангуляционные работы по определению длины дуг меридианов и параллелей проводились учеными разных стран (см. п. 1.2 и 2.1). Геофизический (гравиметрический) метод. Геофизика – это наука, изучающая физические свойства Земли в целом и процессы, происходящие в ее геосферах. Этот метод основан на измерении величин, характеризующих земное поле силы тяжести, и их распределение на поверхности Земли. Измерения потенциала силы тяжести, выполняемые на поверхности Земли, позволяют вычислять сжатие Земли с большей точностью, чем астрономо-геодезическим методом. Преимуществом этого метода является то, что его можно использовать на акваториях морей и океанов, где возможности астрономо-геодезического метода ограничены. С именем французского ученого А. Клеро (1713–1765) связано применение гравиметрического метода. В 1743 г. предполагая, что Земля состоит из сфероидальных слоев с общим центром, плотность которых возрастает к центру, он получил формулу для вычисления ускорения силы тяжести в любой точке Земли:
где gφ; gэ; gn – ускорение силы тяжести, соответственно, на определяемой широте φ, на экваторе и на полюсе. Если в имеющуюся формулу подставить числовые значения gэ и gn, полученные путем измерений, то формула примет вид: g φ = 978, 030 (1+ 0,005302 sin2 φ). Развитие космического метода относится к периоду освоения космического пространства с помощью ИСЗ. Этот метод основан на наблюдениях за ИСЗ и определении координат в заданный момент времени. Выявление отклонений реальных орбит ИСЗ от предвычисленных, вызванных неравномерным распределением масс в земной коре, позволяет уточнить представление о гравитационном поле Земли, а, следовательно, о ее форме и размерах (см. п. 7.5).
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 628; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.210.196 (0.008 с.) |


 , которая совпадает с осью вращения Земли; большой полуосью (экваториальный радиус)
, которая совпадает с осью вращения Земли; большой полуосью (экваториальный радиус)  , которая перпендикулярна оси вращения Земли и полярным сжатием
, которая перпендикулярна оси вращения Земли и полярным сжатием 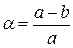 .
. Элементы земного эллипсоида, рассчитан–ные Деламбром (1800), Бесселем (1841), Хейфордом (1909) и другими учеными неоди–наковы, так как вычислены по геодезическим измерениям разных по протяженности дуг ме–ридианов и параллелей.
Элементы земного эллипсоида, рассчитан–ные Деламбром (1800), Бесселем (1841), Хейфордом (1909) и другими учеными неоди–наковы, так как вычислены по геодезическим измерениям разных по протяженности дуг ме–ридианов и параллелей. Земной эллипсоид, принятый для обработки геодезических измерений и установления единой государственной системы координат называется референц-эллипсоидом.
Земной эллипсоид, принятый для обработки геодезических измерений и установления единой государственной системы координат называется референц-эллипсоидом.
 ,
,


