
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Топография с основами геодезии. Курс лекцийСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Топография с основами геодезии. КУРС ЛЕКЦИЙ ВВЕДЕНИЕ Предмет и задачи топографии и геодезии Топография (от греч. topos – место, местность и grapho – пишу), научно-техническая дисциплина, изучающая земную поверхность и размещенные на ней объекты в геометрическом отношении, с целью изображения их на топографических картах, планах и профилях. Главной задачей топографии является – создание топографических карт и планов. Основной метод изучения земной поверхности – топографическая съемка. Топографическая съемка – это комплекс (совокупность) полевых измерений на местности и камеральных работ для создания топографических карт земной поверхности в заданном масштабе. Термин «топография» часто принимают эквивалентным термину «геодезия», что в переводе с греческого означает землеразделение (geodaisia, ge – земля и daizo – делю на части, разделяю). С современной точки зрения, геодезия является наукой о методах изучения формы и размеров Земли, изображения ее поверхности на картах, а также о методах специальных измерений необходимых для решения инженерных, экономических и других задач. В процессе своего развития геодезия разделилась на ряд связанных между собой самостоятельных научных дисциплин – высшую геодезию, топографию, космическую геодезию, фототопографию и инженерную геодезию. К задачам высшей геодезии относятся определение фигуры и размеров Земли, изучение гравитационного поля Земли, определение на Земле взаимного положения точек, составляющих государственную геодезическую сеть (ГГС), необходимую для изучения земной поверхности и точного ее картографирования на плоскости с учетом возникающих при этом искажений. В 1960-х гг. начал интенсивно развиваться новый раздел высшей геодезии – космическая (спутниковая) геодезия. Задачами данной дисциплины являются исследование основных параметров и внешнего гравитационного поля Земли и других планет Солнечной системы, а также определение координат пунктов земной поверхности в геоцентрической системе координат. Фототопография (аэрофототопография) занимается изучением методов и средств создания топографических карт и планов по фотоснимкам поверхности Земли. Аэрофототопографиятесно связана с фотограмметрией. Фотограмметрия – это научная и инженерно-техническая дисциплина, занимающаяся определением формы, размеров и положения различных объектов местности путем измерения их изображения на фотоснимках. Инженерная геодезия, имеющая прикладное значение, представляет комплекс геодезических работ, выполняемых при изысканиях, строительстве и эксплуатации различных сооружений, а также при монтаже оборудования, при наблюдениях за вертикальными и горизонтальными смещениями инженерных сооружений. В своей теории и практическом применении топография использует достижения целого ряда наук: математики, физики, электроники и др. Большое значение топография имеет для изучения географических дисциплин картографии, геоморфологии, почвоведения, геологии, ландшафтоведения и др. В задачу картографии входят вопросы теории и способов изображения на плоскости частей земной поверхности (отдельных государств, материков, земного шара), а также разработка методов и процессов создания и использования различных карт. Значение топографии для науки и практики трудно переоценить. Особенно велика роль топографии при картографировании природной среды. Описания местности не могут заменить топографических карт и планов, на которых наглядно передаются все подробности местности. Топографические карты являются необходимыми при проведении полевых экспедиционных работ и представляются незаменимыми при выполнении картометрических исследований. Созданные топографические карты являются основным материалом для составления общегеографических карт. Большая роль принадлежит топографии и геодезии в народном хозяйстве. Геодезические измерения предшествуют многим основным видам деятельности в развитии народного хозяйства страны. Геодезические измерения производятся на поверхности Земли и в ее недрах, в приземных слоях атмосферы, в океанах и морях. Геодезические изыскания выполняются на стадии проектирования, строительства и реконструкции населенных пунктов, железных и шоссейных дорог, тоннелей, мостов, магистральных нефте- и газопроводов и других объектов, а также для наблюдений за сдвигом и осадкой крупных сооружений. Огромное значение геодезические работы имеют в сельском хозяйстве, с которым геодезия связана с древних времен. Проведение землеустроительных работ, направленных на рациональное использование земельных ресурсов, учет сельскохозяйственных земель и их качества, строительство гидромелиоративных и гидротехнических сооружений – все это тесно связано с геодезическими измерениями. Геологические изыскания начинаются и заканчиваются с использованием геодезических материалов и измерений. Строительство метро, шахт и карьеров невозможно без проведения геодезических работ, которые выполняют горные геодезисты – маркшейдеры. Особая роль принадлежит геодезии в вопросах обороноспособности государства. Топографические карты используются для изучения местности, при разработке военных операций и отображения на них боевой обстановки. Единицы мер в топографии и геодезии Совокупность единиц физических величин, принятых в государстве для измерений называется системой мер. При производстве геодезических измерений единицей угла служит градус, равный 1/360 части окружности или 1/90 части прямого угла (1º = 60΄, 1΄= 60΄΄). Пример: 11º 07´ 56´´. Наряду с градусной системой мер в некоторых странах употребляется десятичная или децимальная система, в которой прямой угол делят на 100 частей, называемых градами. Град делится на 100 минут или сантиград, а минута – на 100 секунд. Пример: 46g 68s 98ss или 46,6898 g. Значение угла может быть выражено в радианной мере. Радиан ρ – центральный угол, соответствующий длине дуге окружности, равной ее радиусу. Величина радиана – ρ = 57º 17΄ 44,8΄΄ или ρ° ≈ 57,3; ρ΄ ≈ 3438; ρ΄΄ ≈ 206 265, где ρ°, ρ΄, ρ΄΄ – число градусов, минут, секунд в радиане. Единица длины – метр (м). За метр принята длина “архивного метра” платинового жезла, хранящегося в международном бюро мер и весов во Франции. Длина жезла была принята равной одной десятимиллионной части четверти Парижского меридиана. В 1889 г. была изготовлена 31 копия «архивного метра», две из которых были переданы в Россию. Для создания надежно воспроизводимого эталона метра в 1960 г. было решено выражать его через длину световых волн. В 1983 г. принято новое определение метра, согласно которому метр равен расстоянию, проходящему в вакууме плоской электромагнитной волной за 1/299 792 458 доли секунды. Кратные единицы метра –1 км = 1000 м; 1 дм = 0,1 м; 1 см = 0,01 м и 1мм = 0,001 м. Единица площади – квадратный метр (м2). Кратные единицы – 1км2 = 1 000 000 м2 ; 1 см2 = 0,0001 м2 ; 10 000 м2 = 1 га; 1 км2 = 100 га. Единица времени – секунда (s). Секунда равна 9 192 631 770 периодам излучения, соответствующего перехода между двумя сверхтонкими уровнями основного состояния атома Цезия-133. 1m(мин) = 60s; 1h (час) = 3600 s. Единица температуры – градус по шкале Цельсия (°С). Единицей массы служит килограмм (кг).Копия представляет платиново-иридиевую гирю – цилиндр диаметром и высотой 39 мм. Единица силы – ньютон (Н). 1Н равен силе, сообщающей телу массой 1кг ускорение 1 м/сек2в направлении действия силы. Единицей измерения давления служит паскаль (Па).Паскаль равен давлению, вызываемому силой 1Н равномерно распределенной по нормальной к ней поверхности площадью 1м2. 1 Па= 9,87 × 10 –6 атм. или 7,60 × 10–3 мм.рт.ст. Давление, равное 1013 г Па на уровне моря на широте 45° принято считать нормальным. ОБЩИЕ СВЕДЕНИЯ
Форма и размеры Земли Физическая поверхность Земли представляет собой сочетание бесконечно большого числа неровностей. Она состоит из океанов, морей и материков с островами. Поверхность океанов в их спокойном состоянии ровная, а суша, составляющая только 29 % от общей площади Земли, представляет собой сложные сочетания гор, возвышенностей, равнин и низменностей. Поэтому поверхность Земли не имеет математического выражения, хотя для решения задач науки и практики требуется знать пространственное положение ее точек. Устанавливать их удобно относительно вспомогательной поверхности, близкой к реальной (физической) поверхности Земли. Такую поверхность называют поверхностью относимости, за которую принимается основная уровенная поверхность Земли, в каждой точке которой нормаль совпадает с направлением отвесной линии (с направлением силы тяжести). Это поверхность воды океанов и открытых морей, находящаяся в спокойном состоянии и мысленно продолженная под материками так, что к ней отвесные линии перпендикулярны во всех точках на Земле. Выбор поверхности воды океанов и морей за уровенную поверхность Земли, объясняется тем, что поверхность открытых водных пространств занимает 71 % общей площади Земли. В 1873 г. немецкий физик И. Б. Листинг назвал эту поверхность поверхностью геоида. Однако и фигура геоида сложна и строго неопределима, поскольку зависит от малоизученного распределения масс внутри Земли. Поэтому поверхность геоида не соответствует поверхности ни одной правильной математической фигуры, что не позволяет проводить расчеты, связанные с обработкой геодезических измерений на земной поверхности. По предложению ученого М. С. Молоденского вместо геоида в качестве промежуточной поверхности относимости используется квазигеоид, выполняющий роль «уровня моря». Положение его поверхности рассчитывается на основе гравиметрических измерений (см. 2.2). Поверхности квазигеоида и геоида совпадают с поверхностью Мирового океана и различаются по высоте на суше не более чем на 2,5 м. Геоид и квазигеоид по форме близко подходят к правильной математической фигуре – эллипсоиду вращения. Поэтому в качестве основной уровенной поверхности при обработке геодезических измерений, выполняемых на земной поверхности принята поверхность эллипсоида вращения, представляющего собой фигуру, полученную в результате вращения эллипса вокруг его малой оси (земной) эллипсоид. Угол между отвесной линией pq к поверхности геоида в данной точке и нормалью mn к поверхности эллипсоида называется уклонением отвесной линии e (рис. 2.1). В среднем, значение e составляет 3–4″, а в местах аномалий достигает десятков секунд.
Рис. 2.1
Земной эллипсоид характеризуется следующими основными элементами (рис. 2.2.): малой полуосью (полярный радиус)
На территории СССР пользовались эллипсоидом Ф. В. Бесселя до 1946 г. Однако этот эллипсоид был рассчитан в основном по данным Западной Европы. На Дальнем Востоке его поверхность сильно уклонялась от поверхности Земли. Более точные результаты размеров земного эллипсоида были получены в 1940 г.Ф. Н. Красовским и А. А. Изотовым по результатам астрономо-геодезических работ, выполненных на территории СССР, Западной Европы и США. Размеры земного эллипсоида, получившего название «референц-эллипсоида Красовского», были приняты для геодезических и картографических работ на всей территории СССР. Отклонения поверхности референц-эллипсоида Красовского от поверхности геоида не превышают 150 м. Точкой ориентирования референц-эллипсоида Красовского является центр круглого зала Пулковской обсерватории, широта В0 и долгота L0 которого определены из астрономических наблюдений и приняты исходными, а поверхность эллипсоида совмещена со средним уровнем воды в Финском заливе и отмечена на Кронштадском футштоке. В настоящее время основные геометрические параметры общеземного эллипсоида определяются более точными методами с использованием искусственных спутников Земли. Для сравнения в табл. 2.1 приведены размеры земного эллипсоида, определенные Бесселем, Красовским и в глобальной геоцентрической системе координат WGS – 84 (World Geodetic System 1984). Таблица 2.1. Размеры земного эллипсоида
При картографических работах (составление карт мелких масштабов) Землю достаточно принимать за шар, объем которого равен объему земного сфероида. Исходя из размеров эллипсоида Красовского R = 6 371 110 м.
2.2. Методы определения формы и размеров Земли Астрономо-геодезический метод. Определение формы и размеров Земли при помощи этого метода основано на использовании градусных измерений, суть которых сводится к определению линейной величины дуг меридианов и параллелей на разных широтах. Первое известное в истории определение длины земного меридиана, выполненное в античное время в Египте принадлежит Эратосфену. По его определениям длина меридианной окружности, равнялась 39 500 км, то есть очень близко к действительной величине меридиана 40 009 км. Ряд допущений, сделанных Эратосфеном, и несовершенный метод линейных измерений (расстояние определялось по длине караванного пути, измеренное в египетских стадиях (1 стадия может быть приравнена к 157,5 м) привели к приближенным результатам. Однако значение выполненных работ заключается в том, что Эратосфен впервые применил геодезический метод определения размеров Земли и получил довольно удовлетворительные для того времени результаты. Высокая точность измерения значительных по протяженности расстояний обеспечивается методом триангуляции, который был разработан в 1615 г. голландским ученым В. Снеллиусом. Триангуляция (от лат. triangulum – треугольник) – способ определения положения опорных геодезических пунктов А, В, С,… на местности путем построения сети примыкающих друг к другу треугольников, в которых измеряются все углы, а с помощью базиса аb определяется длина выходной стороны АВ в их ряду, длины же других сторон вычисляют по координатам этих пунктов (рис. 2.3).
Рис. 2.3
Триангуляция являлась основным способом создания опорной геодезической сети и градусных измерений до развития и становления космического метода. Триангуляционные работы по определению длины дуг меридианов и параллелей проводились учеными разных стран (см. п. 1.2 и 2.1). Геофизический (гравиметрический) метод. Геофизика – это наука, изучающая физические свойства Земли в целом и процессы, происходящие в ее геосферах. Этот метод основан на измерении величин, характеризующих земное поле силы тяжести, и их распределение на поверхности Земли. Измерения потенциала силы тяжести, выполняемые на поверхности Земли, позволяют вычислять сжатие Земли с большей точностью, чем астрономо-геодезическим методом. Преимуществом этого метода является то, что его можно использовать на акваториях морей и океанов, где возможности астрономо-геодезического метода ограничены. С именем французского ученого А. Клеро (1713–1765) связано применение гравиметрического метода. В 1743 г. предполагая, что Земля состоит из сфероидальных слоев с общим центром, плотность которых возрастает к центру, он получил формулу для вычисления ускорения силы тяжести в любой точке Земли:
где gφ; gэ; gn – ускорение силы тяжести, соответственно, на определяемой широте φ, на экваторе и на полюсе. Если в имеющуюся формулу подставить числовые значения gэ и gn, полученные путем измерений, то формула примет вид: g φ = 978, 030 (1+ 0,005302 sin2 φ). Развитие космического метода относится к периоду освоения космического пространства с помощью ИСЗ. Этот метод основан на наблюдениях за ИСЗ и определении координат в заданный момент времени. Выявление отклонений реальных орбит ИСЗ от предвычисленных, вызванных неравномерным распределением масс в земной коре, позволяет уточнить представление о гравитационном поле Земли, а, следовательно, о ее форме и размерах (см. п. 7.5). Принимаемые за плоскость
Определим разность между длиной касательной S и длиной дуги S1. Выразим угол a в радианах, тогда согласно рис. 2.7 получим, что S = R × tga, а S1 = R×a. Откуда следует, что D S = R(tga -a). (2.1) Центральный угол a по своей величине незначителен. Поэтому при разложении tga в убывающий ряд можно ограничиться вторым членом ряда и пренебречь последующими из-за их незначительности. Тогда
Из формулы S1=R×a получим, что
Из рис. 2.7 видно, что точка D находится на уровенной поверхности и ее высота равна нулю. Определим величину отрезка, характеризующего отклонение точки Q от уровенной поверхности. Для этого рассмотрим прямоугольный треугольник OCQ, откуда (R + D h) ² = S ² + R ². Упростив данное равенство, имеем
Сравнивая формулы 2.3 и 2.4 видно, что значение D h существенно больше D S. Если условно принять радиус Земли постоянным, то можно вычислить расхождения D S между длинами дуг на уровенной поверхности и их проекциями на плоскость, а также отклонения высот точек D h от их положения на поверхности сферы из-за кривизны Земли (табл. 2.2). Таблица 2.2
Значение величины D S возрастает незначительно. При дуге 11 км D S составляет лишь 1:1 000 000 ее длины. Относительная погрешность измерения расстояний современными приборами составляет порядка 1:1 000 000. Поэтому принято считать, что участок радиусом 11 км можно принимать за плоскость, а при определении превышений между точками местности необходимо вводить поправку D h.
2.5. Cистемы координат, применяемые в топографии
Координаты – это величины, определяющие положение любой точки на поверхности или в пространстве в принятой системе координат. Система координат устанавливает начальные (исходные) точки, линии или плоскости для отсчета необходимых величин – начало отсчета координат и единицы их исчисления. В топографии и геодезии наибольшее применение получили системы географических, прямоугольных, полярных и биполярных координат.
Географические координаты – это угловые величины: долгота l и широта j. Географической долготой l называется двугранный угол, заключенный между плоскостью данного меридиана (проходящего через точку В) и плоскостью начального меридиана. За начальный (нулевой) меридиан принят меридиан, проходящий через центр главного зала Гринвичской обсерватории в пределах г. Лондона. Для точки В долгота определяется углом l = WCD. Счет долгот ведут от начального меридиана в обе стороны – на восток и на запад. В связи с этим различают западные и восточные долготы, которые изменяются от 0° до 180°. Географической широтой j называется угол, составленный плоскостью экватора и отвесной линией, проходящей через данную точку. Если Землю принимать за шар, то для точки В (рис. 2.8) широта j определяется углом DCB. Широты, отсчитываемые от экватора к северу, называются северными, а к югу – южными, они изменяются от 0° на экваторе до 90° на полюсах. Географические координаты могут быть получены на основании астрономических наблюдений или геодезических измерений. В первом случае их называют астрономическими, а во втором – геодезическими (L – долгота, B – широта). При астрономических наблюдениях проецирование точек на поверхность относимости осуществляется отвесными линиями, при геодезических измерениях – нормалями. Поэтому величины астрономических и геодезических координат отличаются на величину уклонения отвесной линии. Использование разными государствами различных референц-эллипсоидов приводит к различиям координат одних и тех же пунктов, вычисленных относительно разных исходных поверхностей. Практически это выражается в общем смещении картографического изображения относительно меридианов и параллелей на картах крупного и среднего масштабов.
называются линейные величины – абсцисса и ордината, определяющие положение точки на плоскости относительно исходных направлений.
Прямая ХХ (ось абсцисс) совмещается с направлением меридиана, проходящего через начало координат, или с направлением, параллельным некоторому меридиану. Прямая YY (ось ординат) проходит через точку О перпендикулярную оси абсцисс. В такой системе положение точки на плоскости определяется кратчайшим расстоянием до нее от осей координат. Положение точки А определяется длиной перпендикуляров Xа и Yа. Отрезок Xа называется абсциссой точки А, а Yа – ординатой этой точки. Прямоугольные координаты обычно выражаются в метрах. Осями абсцисс и ординат участок местности в точке О делится на четыре четверти (рис. 2.9). Название четвертей определяется принятыми обозначениями стран света. Четверти нумеруются по направлению хода часовой стрелки: I – СВ; II – ЮВ; III – ЮЗ; IV – СЗ. В табл. 2.3 показаны знаки абсцисс Х и ординат Y для точек, находящихся в разных четвертях и даны их названия. Таблица 2.3
Абсциссы точек, расположенные вверх от начала координат считаются положительными, а вниз от нее – отрицательными, ординаты точек, расположенные вправо – положительными, влево – отрицательными. Система плоских прямоугольных координат применяется на ограниченных участках земной поверхности, которые могут быть приняты за плоские.
Система биполярных координат (рис. 2.11) представляет собой два выбранных неподвижных полюса О1 и О2, соединенные прямой – полярной осью. Данная система координат позволяет определить положение точки М относительно полярной оси на плоскости при помощи двух углов b1 и b2, двух радиусов-векторов r 1 и r 2 или их комбинаций. Если известны прямоугольные координаты точек О1 и О2, то положение точки М можно вычислить аналитическим способом (см. 7.4).
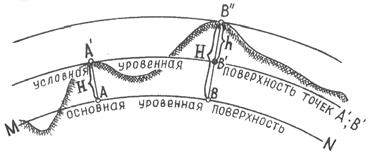
. Высоты точек земной поверхности. Для определения положения точек физической поверхности Земли недостаточно знать только плановые координаты X, Y или l, j, необходима третья координата – высота точки Н. Высотой точки Н (рис. 2.12) называется расстояние по отвесному направлению от данной точки (А ´; В ´´) до принятой основной уровенной поверхности MN. Числовое значение высоты точки называется отметкой. Высоты, отсчитываемые от основной уровенной поверхности MN, называют абсолютными высотами (АА ´; ВВ´´), а определяемые относительно произвольно выбранной уровенной поверхности – условными высотами (В´В´´). Разность высот двух точек или расстояние по отвесному направлению между уровенными поверхностями, проходящими через две любые точки Земли называется относительной высотой (В´В´´) или превышением этих точек h. В России, Украине, Беларуссии принята Балтийская система высот 1977 г. Счет высот ведется от уровенной поверхности, совпадающей со средним уровнем воды в Финском заливе, от нуля Кронштадского футштока.
2.6. Ориентирование направлений в топографии
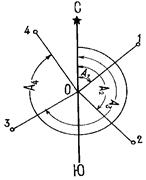
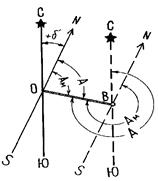
Ориентировать линию местности – значит определить ее направление относительно другого направления принятого за исходное. В топографии и геодезии исходными направлениями для ориентирования приняты географический меридиан, магнитный меридиан и осевой меридиан геодезической зоны, которые на топографических картах соответственно обозначаются: – линией со звездочкой (ê); – линией со стрелкой () и линией с угольником на конце (U). Направление географического меридиана получают из астрономических наблюдений, а направление магнитного меридиана определяет свободно подвешенная и уравновешенная магнитная стрелка. Магнитная ось стрелки в каждой точке земной поверхности совпадает с направлением магнитного меридиана этой точки. Географическим азимутом А направления, называется горизонтальный угол А, измеренный по ходу часовой стрелки от северного направления географического меридиана, проходящего через данную точку до ориентируемой линии (рис. 2.13). По абсолютному значению азимуты изменяются от 0 до 360°. На рисунке горизонтальные углы А 1, А 2, А 3, А 4 будут географическими азимутами ориентируемых направлений О1; О2; О3; О4. Точка О – начало ориентируемых направлений; а линия СЮ – географический меридиан точки О.
Магнитным азимутом направления называется горизонтальный угол А м между северным направлением магнитного меридиана и направлением данной линии, отсчитываемый по ходу часовой стрелки (рис. 2.14). Вследствие не совпадения географических и магнитных полюсов магнитный и географический меридианы в данной точке земной поверхности образуют между собой угол d, называемый склонением магнитной стрелки (рис. 2.14). Магнитное склонение может быть восточным – положительным, если северное направление магнитного меридиана находится к востоку от географического и западным – отрицательным, если северное направление магнитного меридиана проходит к западу от географического. Зависимость между географическим и магнитным азимутами выражается формулой А = А м + d. Склонение магнитной стрелки изменяется в зависимости от места и времени. Различают: суточные, годовые и вековые изменения склонения. Кроме того, величина склонения изменяется под влиянием магнитных бурь, связанных с полярным сиянием, солнечной активности, землетрясений, в районах магнитных аномалий и т. д. Суточные колебания склонения магнитной стрелки не превышают 5–15¢. Вследствие этого, ориентирование по магнитному азимуту проводится лишь в тех случаях, когда не требуется большая точность. В топографии и геодезии применяется также ориентирование направлений относительно северного направления оси абсцисс в системе прямоугольных координат. Угол, отсчитываемый от северного направления оси абсцисс или линии параллельной ему до данного направления, по ходу часовой стрелки называется дирекционным углом a (рис. 2.15). Дирекционный угол изменяется от 00 до 3600.
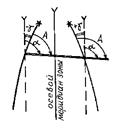
Угол между географическим меридианом данной точки и северным направлением оси абсцисс (вертикальной линией координатной сетки) называется сближением меридианов g (рис. 2.15). Сближение меридианов бывает восточным со знаком плюс и западным со знаком минус. При восточном сближении меридианов, линии параллельные осевому меридиану отклоняются к востоку от географического меридиана, проходящего через эту точку, а при западном – к западу. Зависимость между географическим азимутом и дирекционным углом выражается формулой А = a + g. Для того чтобы перейти от дирекционного угла к магнитному азимуту необходимо знать две величины – склонение магнитной стрелки и сближение меридианов. Данные об этих величинах в виде графика и текста помещаются под южной рамкой топографической карты. Магнитный азимут равен разности дирекционного угла и поправки направления А м = a – П. Поправка направления П – это угол между магнитным меридианом и северным направлением оси абсцисс. Поправка вычисляется по формуле Иногда ориентирование линии выражается острыми углами – румбами r. Румбом называют острый угол, отсчитываемый от ближайшего направления меридиана (северного или южного) до данной линии (рис. 2.16). Румбы имеют значения от 0° до 90° и сопровождаются названием четверти в которой проходит линия. Румбы переводят в азимуты и дирекционные углы и наоборот (табл. 2.4). Таблица 2.4
Зависимость между азимутами или дирекционными углами и румбами линий, расположенных в разных четвертях, устанавливают по формулам.
Системами координат
В геодезии угловые измерения выполняются в полярной системе координат, а нанесение на карту пунктов и объектов местности более точно производится по их прямоугольным координатам. Перевычисление полярных координат к прямоугольным и наоборот производится по формулам прямой и обратной геодезических задач(рис. 2.17). Прямая геодезическая задачасостоит в том, что по известным координатам точки А (ХА; YА), горизонтальному проложению S линии АВ и дирекционному углу a, вычисляют приращения координат D х; D у и координаты точки В (ХВ; YВ). Приращениями координат D х и D у называются разности координат конечной В и начальной А точек линии АВ. Значения приращений определяются из прямоугольного треугольника АВС по заданным S и a: D х = S cos a; D у = S sin a. В зависимости от названия четверти прямоугольной системы координат приращения D х и D у имеют определенные знаки (см. табл. 2.3). Координаты конечной точки В вычисляются по формулам: ХВ = ХА + D х; YB = YA + D у.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1674; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.035 с.) |


 , которая совпадает с осью вращения Земли; большой полуосью (экваториальный радиус)
, которая совпадает с осью вращения Земли; большой полуосью (экваториальный радиус)  , которая перпендикулярна оси вращения Земли и полярным сжатием
, которая перпендикулярна оси вращения Земли и полярным сжатием 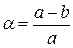 .
. Элементы земного эллипсоида, рассчитан–ные Деламбром (1800), Бесселем (1841), Хейфордом (1909) и другими учеными неоди–наковы, так как вычислены по геодезическим измерениям разных по протяженности дуг ме–ридианов и параллелей.
Элементы земного эллипсоида, рассчитан–ные Деламбром (1800), Бесселем (1841), Хейфордом (1909) и другими учеными неоди–наковы, так как вычислены по геодезическим измерениям разных по протяженности дуг ме–ридианов и параллелей. Земной эллипсоид, принятый для обработки геодезических измерений и установления единой государственной системы координат называется референц-эллипсоидом.
Земной эллипсоид, принятый для обработки геодезических измерений и установления единой государственной системы координат называется референц-эллипсоидом.
 ,
,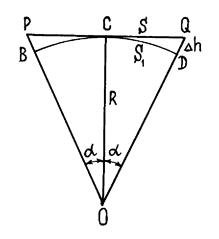 Рассмотрим, для каких по размерам участков местности можно применять ортогональное проецирование, т. е. при которых кривизна Земли может не учитываться в процессе создания карты или плана. На рис. 2.7 изображена часть поверхности Земли в виде дуги BCD радиуса R и ее проекция PQ на плоскость PCQ, где PC = CQ.
Рассмотрим, для каких по размерам участков местности можно применять ортогональное проецирование, т. е. при которых кривизна Земли может не учитываться в процессе создания карты или плана. На рис. 2.7 изображена часть поверхности Земли в виде дуги BCD радиуса R и ее проекция PQ на плоскость PCQ, где PC = CQ. . Подставим это значение в формулу 2.1. В результате получим, что
. Подставим это значение в формулу 2.1. В результате получим, что . (2.2)
. (2.2)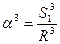 и заменим a в формуле 2.2. Окончательно найдем, что
и заменим a в формуле 2.2. Окончательно найдем, что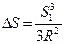 . (2.3)
. (2.3)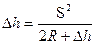 . Ввиду малого значения D h в сравнении с 2R окончательно получим, что
. Ввиду малого значения D h в сравнении с 2R окончательно получим, что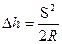 . (2.4)
. (2.4) Географические координаты (рис.
Географические координаты (рис. 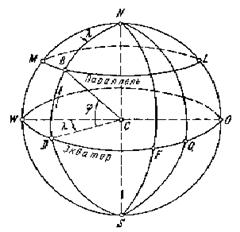 2.8) применяются для определения положения точек поверхности Земли на эллипсоиде (шаре). В этой системе координат исходными являются плоскость начального меридиана и плоскость экватора. Меридианом называют линию сечения эллипсоида плоскостью, проходящей через данную точку и ось вращения Земли. Параллелью называют линию сечения эллипсоида плоскостью, проходящей через данную точку и перпендикулярную земной оси. Параллель, плоскость которой проходит через центр эллипсоида, называется экватором. Через каждую точку, лежащую на поверхности земного шара, можно провести только один меридиан и только одну параллель.
2.8) применяются для определения положения точек поверхности Земли на эллипсоиде (шаре). В этой системе координат исходными являются плоскость начального меридиана и плоскость экватора. Меридианом называют линию сечения эллипсоида плоскостью, проходящей через данную точку и ось вращения Земли. Параллелью называют линию сечения эллипсоида плоскостью, проходящей через данную точку и перпендикулярную земной оси. Параллель, плоскость которой проходит через центр эллипсоида, называется экватором. Через каждую точку, лежащую на поверхности земного шара, можно провести только один меридиан и только одну параллель. Прямоугольными координатами (рис. 2.9)
Прямоугольными координатами (рис. 2.9) В геодезии и топографии принята правая система прямоугольных координат. Это отличает ее от левой системы координат, используемой в математике. Исходными направлениями служат две взаимно перпендикулярные линии с началом отсчета в точке их пересечения О.
В геодезии и топографии принята правая система прямоугольных координат. Это отличает ее от левой системы координат, используемой в математике. Исходными направлениями служат две взаимно перпендикулярные линии с началом отсчета в точке их пересечения О.
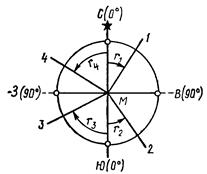
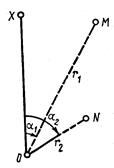 Координаты, началом отсчета которых является какая-либо точка местности, называются полярными. В данной системе координат производится измерение углов ориентирования. На горизонтальной плоскости (рис. 2.10) через произвольно выбранную точку О, называемую полюсом, проводят прямую ОХ – полярную ось. Тогда положение любой точки, например, М будет определяться радиусом – вектором r 1 и углом направления a1, а точки N – соответственно r 2 и a2. Углы a1 и a2 измеряют от полярной оси по ходу часовой стрелки до радиуса-вектора. Полярная ось может располагаться произвольно или совмещаться с направлением какого-либо меридиана, проходящего через полюс О.
Координаты, началом отсчета которых является какая-либо точка местности, называются полярными. В данной системе координат производится измерение углов ориентирования. На горизонтальной плоскости (рис. 2.10) через произвольно выбранную точку О, называемую полюсом, проводят прямую ОХ – полярную ось. Тогда положение любой точки, например, М будет определяться радиусом – вектором r 1 и углом направления a1, а точки N – соответственно r 2 и a2. Углы a1 и a2 измеряют от полярной оси по ходу часовой стрелки до радиуса-вектора. Полярная ось может располагаться произвольно или совмещаться с направлением какого-либо меридиана, проходящего через полюс О.
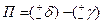 .
. Обратная геодезическая задачазаключается в том, что по известным координатам начальной точки А (ХА; YА) и конечной точки В (ХВ и YВ) определяют горизонтальное проложение S и дирекционный угол a линии АВ (рис. 2.17).
Обратная геодезическая задачазаключается в том, что по известным координатам начальной точки А (ХА; YА) и конечной точки В (ХВ и YВ) определяют горизонтальное проложение S и дирекционный угол a линии АВ (рис. 2.17). Вначале
Вначале 


