Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Внемасштабными условными знакамиСодержание книги Поиск на нашем сайте
Линейные условные знакиизображают линейно вытянутые объекты. Причем длина объектов выражается в масштабе карты, а ширина может быть преувеличена. Положение таких объектов на местности определяется направлением осевой линии. Примером являются: шоссейные и железные дороги, линии электропередач, трубопроводы и др. Примеры определения местоположения объектов, изображенных внемасштабными условными знаками, а так же, что именно принимается за центр внемасштабного условного знака представлены в табл. 3.2. Всего для крупномасштабных карт применяется около 350 графических условных знаков и более 400 сокращенных пояснительных подписей. Однако для работы с картами на конкретной территории достаточно знать несколько десятков знаков. Условные знаки для топокарт издаются в виде сводных таблиц, которые содержат знаки и пояснения к ним, раскрывающие их значения. Для удобства пользования все знаки в таблицах распределены на группы по родственным признакам.
Рельеф земной поверхности и его изображение На топографических картах
Рельеф – это совокупность всех неровностей земной поверхности, различных по своей форме и размерам. Рельеф является основным компонентом ландшафта и оказывает непосредственное влияние на климат, почвообразовательные процессы, распространение флоры и фауны, характер подземных и поверхностных вод и др. Рельеф классифицируют по размерам форми отношению форм рельефа к горизонтальной поверхности. По размерам различают следующие формы рельефа: макро-, мезо-, микро- и нанорельеф. Макрорельеф – крупные формы рельефа с колебаниями высот до нескольких сотен и тысяч метров (горные хребты, горные впадины, вулканические конусы и т. д.). Мезорельеф – средние формы рельефа с амплитудами высот до нескольких десятков метров (холмы, балки, лощины). Микрорельеф – малые формы рельефа, колебания высот не превышают нескольких метров (прирусловые валы, степные блюдца, небольшие котловины и т. д.). Нанорельеф – мелкие формы рельефа, амплитуды высот не превышают нескольких десятков сантиметров. Это – борозды, промоины, незначительные бугры и западины, кочки, мочажины и т. п. По отношению к горизонтальной поверхности формы рельефа подразделяются на положительные, имеющие выпуклую поверхность и возвышающиеся над окружающей местностью, и отрицательные с вогнутой поверхностью, образующие понижения местности. Основные положительные формы рельефа. Холм – отдельная небольшая возвышенность до 200 м высотой над окружающей местностью со сравнительно пологими склонами и слабо выраженным подножием. Увал – пологая и вытянутая возвышенность с относительной высотой до 200 м, с плоской или слегка выпуклой вершинной поверхностью и неясно выраженным подножием. Гора – возвышенность с высотой более 200 м с ясно выраженными крутыми склонами, где отчетливо различается вершина, склоны и подошва. Острая вершина называется пиком. Хребет – горная возвышенность большого протяжения, с крутыми склонами в обе стороны. Седловина – понижение между двумя соседними горными вершинами или возвышенностями. Плато – плоская возвышенность, ограниченная отчетливыми крутыми склонами – уступами. Основные отрицательные формы рельефа. Долина – вытянутая в длину вогнутая форма рельефа с ясно выраженными склонами, имеющая уклон в одном направлении. Различают дно (ложе) и склоны долины. Площадки, вытянутые вдоль долины по склонам и разделенные уступами, называются террасами. Овраг – резко выраженное углубление на равнине с крутыми или обрывистыми склонами и временно действующими водотоками. Овраги имеют уклон в одном направлении и не пересекаются между собой. Балка (лог) – линейно-вытянутое углубление длиной до нескольких десятков километров, имеющее пологие, часто задернованные склоны и плоское дно. Балка представляет позднюю стадию развития оврагов. Лощина – небольшое углубление с пологими слабовыраженными склонами, постепенно переходящими в равнину и имеющую уклон в одном направлении. Котловина – замкнутое со всех сторон, вогнутое понижение местности, различных форм и размеров. Небольшие котловины с незначительной глубиной и плоским дном называются блюдцами или западинами. Формы рельефа характеризуются основными орографическими линиями, которые дают представление о степени его расчлененности и составляющие структуру неровностей местности, так называемые – скелетные линии рельефа. К ним относятся:водораздел, тальвег, бровка, подошва. Водораздел – линия или полоса местности, разделяющая поверхностный сток противоположных склонов возвышенности. Тальвег – линия, соединяющая наиболее низкие точки дна долины. Бровка – линия перегиба склона, ниже которой он становится более крутым. Подошва – линия перегиба склона, ниже которой он становится более пологим. Подошвой называют также подножия гор, холмов, обрывов. Изображение рельефа на топокартах должно быть наглядным, отражать количественные характеристики неровностей местности (абсолютные высоты, превышения точек, крутизну склонов и др.). Рельеф на топокартах изображается горизонталями в сочетании с отметками высот и условными обозначениями форм, которые нельзя изобразить горизонталями. Способ изображения рельефа горизонталями позволяет геометрически наиболее точно передать форму рельефа и отразить его особенности. Горизонтали – это кривые линии, соединяющие на карте точки с одинаковыми высотами. Горизонтали представляют проекции сечения местности уровенными поверхностями через определенные высоты (рис. 3.9).
Рис. 3.9. Заданное расстояние между соседними секущими уровенными поверхностями называется высотой сечения рельефа h0 . Расстояние на карте между смежными горизонталями называется заложением s. Высота сечения рельефа зависит от масштаба карты и характера рельефа местности. Нормальной высотой сечения принято считать высоту, равную 0,02 см в масштабе карты. В зависимости от условий рельефа местности для различных масштабов карт установлены стандартные нормальные высоты сечения рельефа. Так, в пределах равнинных территорий для топокарт масштаба 1:10 000 – 2,5 м; 1:25 000 – 5 м; 1:50 000 – 10 м; 1:100 000 – 20 м. Для высокогорных территорийвысота сечения рельефа берется в 2 раза больше нормальной, адля плоскоравнинных – в 2 раза меньше. Горизонтали нормального сечения проводят сплошными линиями коричневого цвета толщиной 0,12–0,15 мм и называют основными или сплошными горизонталями. Для улучшения читаемости рельефа каждая пятая горизонталь (для масштаба 1:10 000 – каждая десятая), вычерчивается утолщенной линией 0,2 – 0,25 мм. Такие горизонтали называются утолщенными. Для отражения форм рельефа, не выражающихся основными горизонталями применяются дополнительные и вспомогательные горизонтали. Дополнительные, или полугоризонтали проводятся в половине основного сечения прерывистыми линиями длиной штрихов 5 мм, а вспомогательные или четвертьгоризонтали – в ¼ высоты сечения длиной штрихов – 2 мм. Формы рельефа, не выражающиеся горизонталями, изображаются специальными условными знаками. Это – обрывы, оползни, осыпи, овраги, промоины, воронки, курганы и др. Изображение элементов местности горизонталями представлено на рис. 3.10.
Горизонтали имеют следующие свойства: 1. Все точки, лежащие на одной горизонтали, имеют одинаковые отметки высот, кратные принятой высоте сечения рельефа. 2. Горизонтали – непрерывные замкнутые линии. Если горизонталь не замыкается внутри карты, то может обрываться только у рамки карты. 3. Горизонтали никогда не пересекаются, т. к. относятся к разным по высоте плоскостям. 4. Горизонтали одного и того же склона имеют внешнее сходство в рисунке. 5. Расстояние между горизонталями характеризует крутизну склона (ската). Для улучшения читаемости рельефа, на карте подписываются абсолютные отметки вершин, седловин, тальвегов, перегибов склонов, а также относительные высоты обрывов, курганов, уступов террас, которые отсчитываются от подошв и бровок.
Рис. 3.10
Рис. 3.11 высот помещается в разрывах линий горизонталей, причем верх цифр всегда направлен в сторону повышения склона (рис. 3.11). Направление ската на топографических картах определяется указателями – бергштрихами, а также отметками горизонталей, отметками высот, расположением водоемов. Бергштрихи – это короткие штрихи (черточки) длиной около 0,8 мм перпендикулярные к горизонталям и направлены всегда свободным концом в сторону понижения склона (см. рис. 3.11). Бергштрихи помещаются на сгибах горизонталей, у вершин, седловин, на склонах, на дне котловин, т. е. в местах затруднительных для чтения. Основными элементами, характеризующими склон, являются: крутизна, которая определяется углом наклона линии к горизонтальной плоскости; направление, соответствующее кратчайшему и наиболее крутому скату; высота – превышение вершины над подошвой; заложение – расстояние на карте между двумя горизонталями.
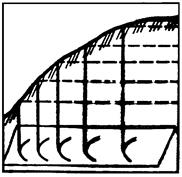
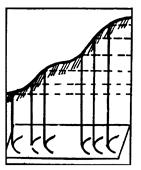
Уклон – безразмерная величина (отношение). На практике уклон выражают в натуральных значениях отношения i = h/s, в промиллях или в процентах. Например: і %о = 0,045, это означает, что на 1 м длины приходится превышение равное 45 мм, или 4,5 %. По взаимному расположению горизонталей на склоне можно определить его крутизну и форму (рис. 3.13). Чем круче склон, тем меньше расстояния между горизонталями и наоборот. Если склон ровный, то горизонтали располагаются на равном расстоянии друг от друга; при вогнутом склоне (рис. 3.13 а) – учащаются к вершине, при выгнутом (рис. 3.13 б) – учащаются к подошве, а при волнистом (рис. 3.13 в) – учащаются или разреживаются в зависимости от количества перегибов склона.
Рис. 3.13 а – вогнутый; б – выпуклый; в – волнистый
В зависимости от крутизны склоны подразделяют на пологие (ν < 5°); покатые (ν от 5 до 20°); крутые (ν от 20 до 45°) и обрывистые (ν > 45°). Крутизна склона на карте определяется по масштабу (графику) заложений, помещенному под южной стороной рамки карты, который строится по формуле: s = h0 сtg ν / М, где s – расстояние между горизонталями; h0 – высота сечения рельефа; М – знаменатель масштаба карты. По карте с горизонталями решают следующие задачи. 1. Определить высоту сечения рельефа, если известны: отметка точки, высота горизонтали и количество промежутков между горизонталями. Для решения задачи (см. рис. 3.14) необходимо определить разность между отметкой точки и значением высоты подписанной горизонтали и разделить на количество промежутков между горизонталями: 2. Определить высоту горизонтали на карте. Данную задачуможно решить двумя способами. Первый способ – находят ближайшую подпись горизонтали, подсчитывают количество промежутков между горизонталями и по высоте сечения рельефа и направлению склона определяют высоту искомой горизонтали. Второй способ – по ближайшей к горизонтали отметке точки, подписанной на карте. При этом высота горизонтали – это ближайшее число в сторону увеличения или уменьшения относительно этой отметки и кратное высоте сечения рельефа. 3. Определить абсолютную отметку точки местности, если: 1) точка местности находится на горизонтали; 2) точка находится в промежутке между горизонталями. В первом случае, когда точка местности находится на горизонтали, то ее абсолютная высота равна отметке этой горизонтали (см. первое свойство горизонталей). Во втором случае, если точка находится в промежутке между горизонталями, то необходимо узнать высоту ближайшей к ней низшей горизонтали Нн.г . и прибавить превышение ∆h данной точки над горизонталью, т. е. H=Нн.г.+ ∆h.
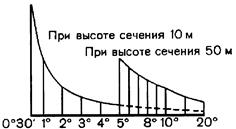
Превышение точки над горизонталью (рис. 3.15) определяется отношением расстояния от низшей горизонтали 210 м (точка А) до определяемой высоты точки С (АС=∆h) к расстоянию между горизонталями АВ, умноженным на высоту сечения hо = 5 м. Из пропорции Превышение точки можно определить на глаз. Для этого устанавливают, какую долю составляет отрезок от горизонтали до точки, от всего расстояния между горизонталями и к высоте горизонтали, в зависимости от направления склона прибавляют или вычисляют превышение точки над горизонталью. 4. Определить превышение (относительную высоту) между пунктами. Для решения этой задачи необходимо определить абсолютные высоты пунктов и вычислить их разность. 5. Определить крутизну на участке между двумя соседними горизонталями. Решение данной задачи можно выполнить двумя способами: по масштабу (графику) заложений и по приближенной формуле. При первом способе в раствор циркуля-измерителя берется расстояние между двумя смежными горизонталями по линии наибольшей крутизны, т. е. по кратчайшему расстоянию между ними и, приложив иглы циркуля к графику заложений, определить угол наклона. График заложений (рис. 3.16) помещается под южной стороной рамки листа топографической карты. В случае очень близкого расположения горизонталей друг к другу, когда затруднительно взять расстояние между ними, крутизну склона определяют между утолщенными горизонталями, пользуясь при этом графиком заложений между утолщенными горизонталями (правый график заложений). Приближенная формула для определения величина угла ν, характеризующего крутизну склона, следующая: 6. Построить профиль местности по направлению, заданному на топографической карте. Горизонтальный масштаб профиля обычно выбирается равным масштабу карты, а вертикальный, для наглядности отображения рельефа – в 5-10 раз крупнее горизонтального. Для построения профиля местности на топографической карте вдоль заданного направления прикладывают полоску бумаги на которой отмечают все пересечения горизонталей и гидрографических объектов местности с линией профиля (рис. 3.17).
Рис. 3.17
У всех точек пересечения подписывают высоты, определенные с топографической карты. Построение профиля выполняют на миллиметровой бумаге. Для этого прочерчивают прямую горизонтальную линию – основание профиля. Линию основания профиля АВ принимают за условный горизонт, таким образом, чтобы она располагалась на 2–3 см ниже минимальной высоты профиля. Затем с полоски бумаги на основание профиля переносят все отмеченные точки. В полученных точках восстанавливают перпендикуляры, на которых откладывают высоты горизонталей, согласно выбранному вертикальному масштабу. При этом следует учитывать, что от всех значений высот точек профиля необходимо вычитать отметку условного горизонта. Отложенные, таким образом, высоты соединяют плавной кривой линией, получая в результате линию профиля местности.
3.8. Определение плановых координат
Для определения плановых координат точек прямоугольных Х,У и географических (геодезических) B, L на топографических картах строят километровую и градусную сетки. В системе географических координат внутренние рамки топографических карт представляют собой отрезки дуг меридианов и параллелей. В вершинах, образуемых ими трапеций, подписаны координаты B и L. Параллельно внутренней рамке построена минутная рамка в виде чередующихся черных и белых полос. Минутные отрезки разделены на 6 частей, т. е. их угловая величина составляет 10΄΄(рис. 3.18). Для нахождения географических координат, необходимо выделить на карте одноминутную трапецию, последовательно соединив для этого, одноименные значения минутных интервалов северной и южной, западной и восточной рамок карты. Таким образом, согласно рис. 3.18 получим одноминутную трапецию с географическими координатами рамок по широте ВС = 54°42¢; ВЮ = 54°41¢ и по долготе L3 = 18°05¢; LВ = 18°06¢. Тогда географические координаты точки 3 определяются путем измерения расстояний S D B ; S D L ; и SB; SL B3 =54°41¢+D B ¢¢; L3 =18°05¢+D L¢¢; Следовательно, географические координаты точки 3 будут иметь значения В3 = 54°41¢18¢¢ и L3 = 18°05¢24¢¢.
Масштаб 1: 10 000
Рис. 3.18
Географические координаты точек можно получить без построения минутных рамок с помощью прямоугольного треугольника путем проецирования, например, точки F (рис. 3.19). Для этого один из катетов прикладывают к минутной рамке так, чтобы второй катет треугольника находился на этой точке. Таким образом, точка F проецируется на соответствующие рамки широт и долгот. Географические координаты точки F будут иметь значения: ВF =54°41¢28¢¢ и LF = 18°05¢15¢¢ (рис. 3. 19).
Рис. 3.19
Аналогично проецирование точки на рамки трапеции можно выполнить путем измерения циркулем кратчайшего расстояния от точки до внутренней рамки карты. Затем этот отрезок переносится на соответствующие минутные рамки, где определяют широту и долготу точки. Для определения прямоугольных координат Х, У на все топографические карты наносят километровую сетку, параллельную осям зональной системы координат (абсцисс и ординат) через расстояния кратные целому числу километров. Полученную сеть квадратов называют километровой сеткой. Линии километровой сетки подписываются между внутренней и минутными рамками, т. е. указаны абсциссы и условные ординаты линий сетки. Километровые линии, ближние к углам внутренней рамки подписываются полностью (первые две цифры – меньшего размера), а остальные сокращенно – только двумя последними цифрами 6065; 6068; 4311; 4314 и 66; 67; 12; 13 (рис. 3.18). Прямоугольные координаты для точки 4находят определением в метрах по поперечному масштабу значений D х и D у, которые прибавляют соответственно к значению абсцисс и ординат, выраженных в километрах. Тогда, согласно рис. 3.18, D х = 454 м, D у = 412 м, а координаты точки 4 будут равны: Х4 = 6 065 000 + 454 = 6 065 454 м; У4 = 4 013 000 + 412 = 4 013 412 м. Измерение на топографических картах ориентирующих углов. Дирекционные углы и географические азимуты на топографических картах измеряются геодезическим транспортиром или при помощи тахеометрического круга. Для измерения углов ориентирования прямого отрезка 5–6 (рис. 3.18) продлим его до пересечения с внутренней (минутной) рамкой карты. С помощью транспортира, центр которого совмещен с точкой пересечения, а нулевой диаметр транспортира – с внутренней рамкой отсчитаем географический азимут А 5-6. При измерении дирекционного угла α5-6 нулевой диаметр транспортира совмещают с вертикальной линией километровой сетки в точке 5΄ или в точке 5 (рис. 3.18). Величину географического А и магнитного Ам азимутов можно определить по измеренному значению дирекционного угла α, пользуясь схемой расположения меридианов. Дирекционный угол α также можно определить по прямоугольным координатам объектов путем решения обратной геодезической задачи. Величина ориентирующих направлений измеряется с точностью до 10-15΄. Однако необходимо отметить, что в связи с неизбежными погрешностями прочерчивания географического меридиана и определяемого направления уменьшается точность измерения углов направления.
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1028; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.57 (0.012 с.) |


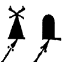



 Для определения абсолютных высот местности некоторые горизонтали имеют подписи высот. Подпись
Для определения абсолютных высот местности некоторые горизонтали имеют подписи высот. Подпись
 Крутизна склона определяется углом наклона n или уклоном i. Уклоном прямой АВ называется отношение высоты сечения hо к заложению s (рис. 3.12), т. е. уклон – это тангенс угла наклона n и определяется по формуле
Крутизна склона определяется углом наклона n или уклоном i. Уклоном прямой АВ называется отношение высоты сечения hо к заложению s (рис. 3.12), т. е. уклон – это тангенс угла наклона n и определяется по формуле  .
. а
а
 б
б
 в
в
 . Зная стандартные высоты сечения рельефа, находим, что в нашем примере высота сечения рельефа для данной карты равняется 5 м.
. Зная стандартные высоты сечения рельефа, находим, что в нашем примере высота сечения рельефа для данной карты равняется 5 м.


 следует, что
следует, что 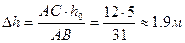 , тогда НС = 210 + 1,9 = 211,9 м.
, тогда НС = 210 + 1,9 = 211,9 м.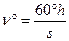 ; где h – превышение (высота сечения рельефа); s – заложение в метрах на местности. Эту формулу можно использовать для определения среднего угла наклона для двух точек, лежащих на одном склоне.
; где h – превышение (высота сечения рельефа); s – заложение в метрах на местности. Эту формулу можно использовать для определения среднего угла наклона для двух точек, лежащих на одном склоне.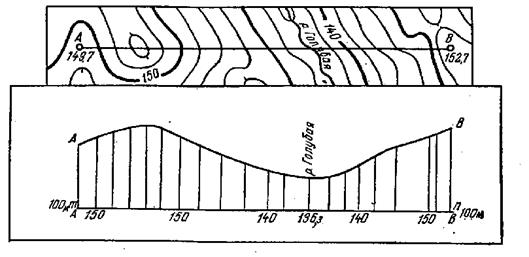
 c помощью измерителя и масштабной линейки.
c помощью измерителя и масштабной линейки.