Векторное поле. Дивергенция.
Похожие статьи вашей тематики
Если каждой точке точке М области простр-ва соответствует нек. вектор  , то говорят, что задано векторное поле. Векторная линия – линия, касательная к которой в кажд. ее точке М имеет напр. соответствующего ей вектора , то говорят, что задано векторное поле. Векторная линия – линия, касательная к которой в кажд. ее точке М имеет напр. соответствующего ей вектора  . Векторная трубка – совокупность всех вект. линий поля, проходящих через нек. замкнутую кривую. Изучение вект. поля обычно начинают с изучения расположения его вект. линий. Векторные линии поля . Векторная трубка – совокупность всех вект. линий поля, проходящих через нек. замкнутую кривую. Изучение вект. поля обычно начинают с изучения расположения его вект. линий. Векторные линии поля  описываются сист. дифф. ур-ний вида описываются сист. дифф. ур-ний вида  . Действительно, пусть PQ – векторная линия поля, . Действительно, пусть PQ – векторная линия поля,  – ее радиус-вектор. Тогда вектор – ее радиус-вектор. Тогда вектор  направлен по касательной к линии PQ в точке М. В силу коллинеарности векторов направлен по касательной к линии PQ в точке М. В силу коллинеарности векторов  и и  следует пропорциональность их проекций, т.е.: следует пропорциональность их проекций, т.е.:  . .
Дивергенция (расходимость) – характеристика вект-го поля, определяющая распределение и интенсивность источников и стоков поля: дивергенцией  в точке М наз-ся скаляр вида в точке М наз-ся скаляр вида  и обозначается: и обозначается: 
Св-ва дивергенции: 1. если  - пост. вектор, то - пост. вектор, то  . .
2.  , где с=const. , где с=const.
3.  , т.е. дивергенция суммы 2-х векторных ф-ций равна сумме дивергенции слангаемых. , т.е. дивергенция суммы 2-х векторных ф-ций равна сумме дивергенции слангаемых.
4. если U – скал. ф-ция,  - вектор, то - вектор, то  . .
 (1). Дивергенцией векторного поля в точке М наз-ся предел отношения потока поля через (замкнутую) пов-ть S, окружающую точку М, к объему тела, ограниченного этой пов-тью, при условии, что вся пов-ть стягивается в точку М ( (1). Дивергенцией векторного поля в точке М наз-ся предел отношения потока поля через (замкнутую) пов-ть S, окружающую точку М, к объему тела, ограниченного этой пов-тью, при условии, что вся пов-ть стягивается в точку М ( ). Это определение эквивав. ). Это определение эквивав.  . Исходя из физ. смысла потока, можно сказать, что . Исходя из физ. смысла потока, можно сказать, что  точка М представ-т собой источник, откуда жидкость вытекает; при точка М представ-т собой источник, откуда жидкость вытекает; при  точка М есть сток, поглощающий жидкость. Как следует из (1) точка М есть сток, поглощающий жидкость. Как следует из (1)  хар-ет мощность источника или стока в т.М. Это и есть физ. смысл дивергенции. Ясно, что если в объеме V, ограниченном замкн. пов-тью S, нет ни источников, ни стоков, то хар-ет мощность источника или стока в т.М. Это и есть физ. смысл дивергенции. Ясно, что если в объеме V, ограниченном замкн. пов-тью S, нет ни источников, ни стоков, то  Векторное поле, в кажд. т. кот. див. поля =0, Векторное поле, в кажд. т. кот. див. поля =0,  , наз-ся соленоидальным (трубчатым). , наз-ся соленоидальным (трубчатым).
Пример: найти див. поля лин. скоростей v жидкости, вращ-ся как ТВ. тело вокруг неподв. оси с пост. углов. скор.  . Решение: примем ось вр. жидк. за ось Oz. Тогда, как, . Решение: примем ось вр. жидк. за ось Oz. Тогда, как,  . Имеем: . Имеем:  . Поле . Поле  - соленоидальное. - соленоидальное.
Поток векторного поля.
Пусть вект. поле образовано вектором  . Представим, что нек. пов-ть S нах-ся в потоке и пропускает жикость. Подсчитаем кол-во жидк., кот. протекает через пов-ть S. . Представим, что нек. пов-ть S нах-ся в потоке и пропускает жикость. Подсчитаем кол-во жидк., кот. протекает через пов-ть S.
Выберем опред сторону пов-ти S. пусть  - единичный вектор нормали к рассматриваемой стороне пов-ти S. Разобьем пов-ть на эл-ные площ-ки - единичный вектор нормали к рассматриваемой стороне пов-ти S. Разобьем пов-ть на эл-ные площ-ки  . Выберем в кажд. площ-ке т. . Выберем в кажд. площ-ке т.  и вычислим зн-ния вектора скор. и вычислим зн-ния вектора скор.  в кажд. точке. Будем приближенно считать кажд. площ-ку плоской, а в кажд. точке. Будем приближенно считать кажд. площ-ку плоской, а  пост. по модулю и одинаково направленным в кажд. т-ке площ-ки. Тогда за ед. вр. через пост. по модулю и одинаково направленным в кажд. т-ке площ-ки. Тогда за ед. вр. через  протекает кол-во жидк., протекает кол-во жидк.,  , где , где  - площ. i-ой площ-ки, - площ. i-ой площ-ки,  - высота i-ого цилиндра с образующей - высота i-ого цилиндра с образующей  . Но . Но  явл-ся проекцией явл-ся проекцией  на нормаль на нормаль  : :  = =  , ,  - единичный вектор нормали к пов-ти в т. - единичный вектор нормали к пов-ти в т.  . След-но, общее кол-во жидк., протекающее через всю пов-ть S за ед. вр., найдем вычислив сумму . След-но, общее кол-во жидк., протекающее через всю пов-ть S за ед. вр., найдем вычислив сумму  . .
Независимо от физ. смысла поля  полученный инт-л наз-ют потоком вект. поля. полученный инт-л наз-ют потоком вект. поля.
Потоком вект. поля  через пов-ть S – инт-л по пов-ти от скал. произв. вектора поля на ед. вектор нормали к поверхности, т.е.: через пов-ть S – инт-л по пов-ти от скал. произв. вектора поля на ед. вектор нормали к поверхности, т.е.:  . .
Т.к.  , где , где  - проекции вектора - проекции вектора  на соответств. коорд. оси, то поток вектора: на соответств. коорд. оси, то поток вектора: 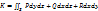 . Поток К вектора . Поток К вектора  есть скал. вел-на. Вел-на К = объему жидк., кот. протекает через пов-ть S за ед. вр. В этом состоит физ.смысл потока. есть скал. вел-на. Вел-на К = объему жидк., кот. протекает через пов-ть S за ед. вр. В этом состоит физ.смысл потока.
 Случай, когда пов-ть замкн. и огран-ет нек. объем V. Тогда поток вектора запис-ся: Случай, когда пов-ть замкн. и огран-ет нек. объем V. Тогда поток вектора запис-ся:  . В эт. случае за напр. вектора . В эт. случае за напр. вектора  обычно берут напр. внешней нормали и говорят о потоке изнутри пов-ти S. Если вект. поле обычно берут напр. внешней нормали и говорят о потоке изнутри пов-ти S. Если вект. поле  есть поле скоростей текущей жидкости, то величина потока К через замкн. пов-ть дает разность между кол-ом жидк-ти, вытек-щей из обл. V и втекающей в нее в ед. вр. (в точках пов-ти S, где вект. линии выходят из объема V, внешняя нормаль образует с вект-ом есть поле скоростей текущей жидкости, то величина потока К через замкн. пов-ть дает разность между кол-ом жидк-ти, вытек-щей из обл. V и втекающей в нее в ед. вр. (в точках пов-ти S, где вект. линии выходят из объема V, внешняя нормаль образует с вект-ом  острый угол и острый угол и  ; в точках, где вект. линии входят в объем, ; в точках, где вект. линии входят в объем,  ). ).
При этом если K>0, то из обл-ти V вытекает больше жидкости, чем в нее втекает. Это озн-ет, что внутри обл. имеются доп. ист-ки. Если К<0, то внутри обл. V есть стоки, поглощающие избыток жидкости. Если К=0, то из обл. V вытекает столько же жидк., сколько в нее втекает в ед. вр.; внутри обл. либо нет ни ист-ов, ни ст-ов, либо они таковы, что их действие взаимно компенсируется.
Пример: найти поток вект-ра  через верхнюю сторону треугольника, полученного при перес-нии плоскости 3x+6y-2z-6=0 с коорд. плоскостями. Решение: через верхнюю сторону треугольника, полученного при перес-нии плоскости 3x+6y-2z-6=0 с коорд. плоскостями. Решение:  . Нормаль к верхней стороне треуг. образует с осью Ox тупой угол, Oy – тупой, Oz – острый. . Нормаль к верхней стороне треуг. образует с осью Ox тупой угол, Oy – тупой, Oz – острый.  , на верхней стороне , на верхней стороне  , поэтому надо выбрать знак -; получим: , поэтому надо выбрать знак -; получим:  . Итак, . Итак, 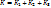 . Находим их: . Находим их:  . .  . . 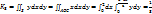 . .  . .
43. Формула Остроградского.
Используя понятия потока и дивергенции вект. поля, запишем ф-лу Остроградского-Гаусса: 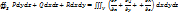 . Рассматривая обл. V, ограниченную замкн. пов-тью S, в вект. поле . Рассматривая обл. V, ограниченную замкн. пов-тью S, в вект. поле  , можно утв-ть, что левая часть ф-лы Остроградского есть поток вектора , можно утв-ть, что левая часть ф-лы Остроградского есть поток вектора  через пов-ть S; подынтегр. ф-ция правой чати ф-лы есть дивергенция вектора через пов-ть S; подынтегр. ф-ция правой чати ф-лы есть дивергенция вектора  . След-но ф-ла Остроградского может выглядеть так: . След-но ф-ла Остроградского может выглядеть так:  (встречается чаще всего). Ф-ла Остроградского-Гаусса означает, что поток вект. поля через замкн. пов-ть S (в напр. внешней нормали, т.е. изнутри) равен 3-ому инт-лу от див. этого поля по объему V, ограниченному данной пов-тью. Используя ф-лу (встречается чаще всего). Ф-ла Остроградского-Гаусса означает, что поток вект. поля через замкн. пов-ть S (в напр. внешней нормали, т.е. изнутри) равен 3-ому инт-лу от див. этого поля по объему V, ограниченному данной пов-тью. Используя ф-лу  , можно дать другое определение дивергенции вект. поля , можно дать другое определение дивергенции вект. поля  в точке М. в точке М.
По теореме о среднем для 3-ного инт-ла имеем:  , ,  – нек. (средняя) точка области V. Тогда ф-лу можно переписать: – нек. (средняя) точка области V. Тогда ф-лу можно переписать:  . Тогда: . Тогда:  . Пусть пов-ть S стягивается в точку. Тогда . Пусть пов-ть S стягивается в точку. Тогда  и мы получим выр-ние для и мы получим выр-ние для  в точке М: в точке М:  . .
 44. Формула Стокса. 44. Формула Стокса.
Пусть  - граница этой пов-ти (нарисуй!!!). Пусть всякая прямая || оси Oz пересекает пов-ть в одной точке. Пусть в кажд. точке пов-ти определен единичный вектор нормали: - граница этой пов-ти (нарисуй!!!). Пусть всякая прямая || оси Oz пересекает пов-ть в одной точке. Пусть в кажд. точке пов-ти определен единичный вектор нормали: 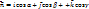 . В кажд. точке пов-ти определен вектор . В кажд. точке пов-ти определен вектор  . При указанных условиях имеет место так называемая ф-ла Стокса: . При указанных условиях имеет место так называемая ф-ла Стокса:  . .  . Этот инт-л наз-ся циркуляцией вект-ра . Этот инт-л наз-ся циркуляцией вект-ра  по этому контуру. Итак циркуляция вект. по этому контуру. Итак циркуляция вект.  по границе λ пространственной обл. σ равна потоку вихря векторя по границе λ пространственной обл. σ равна потоку вихря векторя  по самой пов-ти σ, причем направление обхода контура должно быть согласовано с ориентацией пов-ти. по самой пов-ти σ, причем направление обхода контура должно быть согласовано с ориентацией пов-ти. 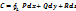 -еще один способ выч-ния циркуляции вектора -еще один способ выч-ния циркуляции вектора  по нек. контуру. по нек. контуру.
Оператор Гамильтона.
Действия взятия градиента, дивергенции и ротора наз-ся векторными операциями 1-го порядка (в них уч. 1-ые произв). Их удобно записывать с пом. оператора Гамельтона:  . Применяя опретор Гамильтона, получим дифф. операции 1-го порядка: . Применяя опретор Гамильтона, получим дифф. операции 1-го порядка:
1.  . .
2.  . .
3.  . .
Оператор Лапласа.
Оператор Лпласа – дифф. оператор, действующий в лин. простр-ве гладких ф-ций и обозначаемый символом  . Ф-ции F он ставит в соответствие ф-цию: . Ф-ции F он ставит в соответствие ф-цию:  . Оператор Лапласа . Оператор Лапласа  послед-ному взятию градиента и дивергенции послед-ному взятию градиента и дивергенции  , т.о. значение оператора Лапласа в точке может быть истолковано как плотность источников (стоков) потенциального , т.о. значение оператора Лапласа в точке может быть истолковано как плотность источников (стоков) потенциального 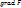 в этой точке. В декартовой системе координат оператор Лапласа часто обозначается следующим образом в этой точке. В декартовой системе координат оператор Лапласа часто обозначается следующим образом  , то есть в виде скалярного произведения оператора набла на себя. , то есть в виде скалярного произведения оператора набла на себя.
|



 , то говорят, что задано векторное поле. Векторная линия – линия, касательная к которой в кажд. ее точке М имеет напр. соответствующего ей вектора
, то говорят, что задано векторное поле. Векторная линия – линия, касательная к которой в кажд. ее точке М имеет напр. соответствующего ей вектора  . Векторная трубка – совокупность всех вект. линий поля, проходящих через нек. замкнутую кривую. Изучение вект. поля обычно начинают с изучения расположения его вект. линий. Векторные линии поля
. Векторная трубка – совокупность всех вект. линий поля, проходящих через нек. замкнутую кривую. Изучение вект. поля обычно начинают с изучения расположения его вект. линий. Векторные линии поля  описываются сист. дифф. ур-ний вида
описываются сист. дифф. ур-ний вида  . Действительно, пусть PQ – векторная линия поля,
. Действительно, пусть PQ – векторная линия поля,  – ее радиус-вектор. Тогда вектор
– ее радиус-вектор. Тогда вектор  направлен по касательной к линии PQ в точке М. В силу коллинеарности векторов
направлен по касательной к линии PQ в точке М. В силу коллинеарности векторов  и
и  следует пропорциональность их проекций, т.е.:
следует пропорциональность их проекций, т.е.:  .
. в точке М наз-ся скаляр вида
в точке М наз-ся скаляр вида  и обозначается:
и обозначается: 
 .
. , где с=const.
, где с=const. , т.е. дивергенция суммы 2-х векторных ф-ций равна сумме дивергенции слангаемых.
, т.е. дивергенция суммы 2-х векторных ф-ций равна сумме дивергенции слангаемых. .
. (1). Дивергенцией векторного поля в точке М наз-ся предел отношения потока поля через (замкнутую) пов-ть S, окружающую точку М, к объему тела, ограниченного этой пов-тью, при условии, что вся пов-ть стягивается в точку М (
(1). Дивергенцией векторного поля в точке М наз-ся предел отношения потока поля через (замкнутую) пов-ть S, окружающую точку М, к объему тела, ограниченного этой пов-тью, при условии, что вся пов-ть стягивается в точку М ( ). Это определение эквивав.
). Это определение эквивав.  . Исходя из физ. смысла потока, можно сказать, что
. Исходя из физ. смысла потока, можно сказать, что  точка М представ-т собой источник, откуда жидкость вытекает; при
точка М представ-т собой источник, откуда жидкость вытекает; при  точка М есть сток, поглощающий жидкость. Как следует из (1)
точка М есть сток, поглощающий жидкость. Как следует из (1)  хар-ет мощность источника или стока в т.М. Это и есть физ. смысл дивергенции. Ясно, что если в объеме V, ограниченном замкн. пов-тью S, нет ни источников, ни стоков, то
хар-ет мощность источника или стока в т.М. Это и есть физ. смысл дивергенции. Ясно, что если в объеме V, ограниченном замкн. пов-тью S, нет ни источников, ни стоков, то  Векторное поле, в кажд. т. кот. див. поля =0,
Векторное поле, в кажд. т. кот. див. поля =0,  , наз-ся соленоидальным (трубчатым).
, наз-ся соленоидальным (трубчатым). . Решение: примем ось вр. жидк. за ось Oz. Тогда, как,
. Решение: примем ось вр. жидк. за ось Oz. Тогда, как,  . Имеем:
. Имеем:  . Поле
. Поле  - соленоидальное.
- соленоидальное. - единичный вектор нормали к рассматриваемой стороне пов-ти S. Разобьем пов-ть на эл-ные площ-ки
- единичный вектор нормали к рассматриваемой стороне пов-ти S. Разобьем пов-ть на эл-ные площ-ки  . Выберем в кажд. площ-ке т.
. Выберем в кажд. площ-ке т.  и вычислим зн-ния вектора скор.
и вычислим зн-ния вектора скор.  в кажд. точке. Будем приближенно считать кажд. площ-ку плоской, а
в кажд. точке. Будем приближенно считать кажд. площ-ку плоской, а  , где
, где  - площ. i-ой площ-ки,
- площ. i-ой площ-ки,  - высота i-ого цилиндра с образующей
- высота i-ого цилиндра с образующей  . Но
. Но  :
:  =
=  ,
,  .
. .
. , где
, где  - проекции вектора
- проекции вектора 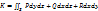 . Поток К вектора
. Поток К вектора  Случай, когда пов-ть замкн. и огран-ет нек. объем V. Тогда поток вектора запис-ся:
Случай, когда пов-ть замкн. и огран-ет нек. объем V. Тогда поток вектора запис-ся:  . В эт. случае за напр. вектора
. В эт. случае за напр. вектора  обычно берут напр. внешней нормали и говорят о потоке изнутри пов-ти S. Если вект. поле
обычно берут напр. внешней нормали и говорят о потоке изнутри пов-ти S. Если вект. поле  есть поле скоростей текущей жидкости, то величина потока К через замкн. пов-ть дает разность между кол-ом жидк-ти, вытек-щей из обл. V и втекающей в нее в ед. вр. (в точках пов-ти S, где вект. линии выходят из объема V, внешняя нормаль образует с вект-ом
есть поле скоростей текущей жидкости, то величина потока К через замкн. пов-ть дает разность между кол-ом жидк-ти, вытек-щей из обл. V и втекающей в нее в ед. вр. (в точках пов-ти S, где вект. линии выходят из объема V, внешняя нормаль образует с вект-ом  ; в точках, где вект. линии входят в объем,
; в точках, где вект. линии входят в объем,  ).
). через верхнюю сторону треугольника, полученного при перес-нии плоскости 3x+6y-2z-6=0 с коорд. плоскостями. Решение:
через верхнюю сторону треугольника, полученного при перес-нии плоскости 3x+6y-2z-6=0 с коорд. плоскостями. Решение:  . Нормаль к верхней стороне треуг. образует с осью Ox тупой угол, Oy – тупой, Oz – острый.
. Нормаль к верхней стороне треуг. образует с осью Ox тупой угол, Oy – тупой, Oz – острый.  , на верхней стороне
, на верхней стороне  , поэтому надо выбрать знак -; получим:
, поэтому надо выбрать знак -; получим:  . Итак,
. Итак, 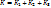 . Находим их:
. Находим их:  .
.  .
. 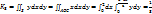 .
.  .
.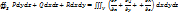 . Рассматривая обл. V, ограниченную замкн. пов-тью S, в вект. поле
. Рассматривая обл. V, ограниченную замкн. пов-тью S, в вект. поле  (встречается чаще всего). Ф-ла Остроградского-Гаусса означает, что поток вект. поля через замкн. пов-ть S (в напр. внешней нормали, т.е. изнутри) равен 3-ому инт-лу от див. этого поля по объему V, ограниченному данной пов-тью. Используя ф-лу
(встречается чаще всего). Ф-ла Остроградского-Гаусса означает, что поток вект. поля через замкн. пов-ть S (в напр. внешней нормали, т.е. изнутри) равен 3-ому инт-лу от див. этого поля по объему V, ограниченному данной пов-тью. Используя ф-лу  ,
,  – нек. (средняя) точка области V. Тогда ф-лу можно переписать:
– нек. (средняя) точка области V. Тогда ф-лу можно переписать:  . Тогда:
. Тогда:  . Пусть пов-ть S стягивается в точку. Тогда
. Пусть пов-ть S стягивается в точку. Тогда  и мы получим выр-ние для
и мы получим выр-ние для  .
. 44. Формула Стокса.
44. Формула Стокса. - граница этой пов-ти (нарисуй!!!). Пусть всякая прямая || оси Oz пересекает пов-ть в одной точке. Пусть в кажд. точке пов-ти определен единичный вектор нормали:
- граница этой пов-ти (нарисуй!!!). Пусть всякая прямая || оси Oz пересекает пов-ть в одной точке. Пусть в кажд. точке пов-ти определен единичный вектор нормали: 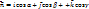 . В кажд. точке пов-ти определен вектор
. В кажд. точке пов-ти определен вектор  . При указанных условиях имеет место так называемая ф-ла Стокса:
. При указанных условиях имеет место так называемая ф-ла Стокса:  .
.  . Этот инт-л наз-ся циркуляцией вект-ра
. Этот инт-л наз-ся циркуляцией вект-ра  по этому контуру. Итак циркуляция вект.
по этому контуру. Итак циркуляция вект.  по границе λ пространственной обл. σ равна потоку вихря векторя
по границе λ пространственной обл. σ равна потоку вихря векторя 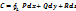 -еще один способ выч-ния циркуляции вектора
-еще один способ выч-ния циркуляции вектора  . Применяя опретор Гамильтона, получим дифф. операции 1-го порядка:
. Применяя опретор Гамильтона, получим дифф. операции 1-го порядка: .
. .
. .
. . Ф-ции F он ставит в соответствие ф-цию:
. Ф-ции F он ставит в соответствие ф-цию:  . Оператор Лапласа
. Оператор Лапласа  послед-ному взятию градиента и дивергенции
послед-ному взятию градиента и дивергенции  , т.о. значение оператора Лапласа в точке может быть истолковано как плотность источников (стоков) потенциального
, т.о. значение оператора Лапласа в точке может быть истолковано как плотность источников (стоков) потенциального 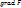 в этой точке. В декартовой системе координат оператор Лапласа часто обозначается следующим образом
в этой точке. В декартовой системе координат оператор Лапласа часто обозначается следующим образом  , то есть в виде скалярного произведения оператора набла на себя.
, то есть в виде скалярного произведения оператора набла на себя.


