
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вираження векторного добутку через координати.Содержание книги
Поиск на нашем сайте
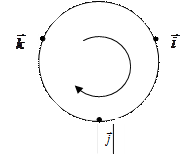
Ми будемо використовувати таблицю векторного добутку векторів
Щоб не помилитися з знаками користуйтеся схемою:
якщо напрямок найкоротшого шляху від першого вектора до другого збігається з напрямком стрілки, то добуток дорівнює третьому векторові, якщо не збігається — третій вектор береться зі знаком «мінус». Нехай задані два вектори
тобто
Отриману формулу можна записати ще коротше:
тому що права частина рівності (3.1) відповідає розкладанню визначника третього порядку по елементах першого рядка. Рівність (3.2) легко запам'ятовується. Деякі застосування векторного добутку. Встановлення колінеарності векторів Якщо
Знаходження площі паралелограма і трикутника Відповідно до означення векторного добутку векторів Визначення моменту сили відносно точки Нехай у точці О — деяка точка простору (див. рис. 19).
рис. 19. З фізики відомо, що моментом сили перпендикулярний площині, що проходить через точки 2) чисельно дорівнює добуткові сили на плече
3) утворює праву трійку з векторами Отже Знаходження лінійної швидкості обертання Швидкість з кутовою швидкістю О — деяка нерухома точка осі (див. рис. 20).
рис. 20. Тема 2.4. Мішаний добуток і його властивості. Визначення мішаного добутку, його геометричний зміст. Розглянемо добуток векторів З'ясуємо геометричний зміст виразу
рис. 21. Маємо: Таким чином, мішаний добуток трьох векторів дорівнює об'єму паралелепіпеда, побудованого на цих векторах, узятому зі знаком «плюс», якщо ці вектори утворюють праву трійку, і зі знаком «мінус», якщо вони утворюють ліву трійку. Властивості мішаного добутку. 1. Мішаний добуток не змінюється при циклічній перестановці його співмножників, тобто Дійсно, у цьому випадку не змінюється ні об'єм паралелепіпеда, ні орієнтація його ребер. 2. Мішаний добуток не міняється при зміні місцями знаків векторного і скалярного множення, тобто Дійсно, 3. Мішаний добуток змінює свій знак при зміні місць будь-яких двох векторів-співмножників, тобто Дійсно, така перестановка рівносильна перестановці співмножників у векторному добутку, що змінює в добутку знак. 4. Мішаний добуток ненульових векторів □ Якщо Допустимо, що це не так. Можна було б побудувати паралелепіпед з обсягом Назад, нехай вектори Вираження мішаного добутку через координати. Нехай задані вектори
Отриману формулу можна записати коротше:
тому що права частина рівності (4.1) являє собою розкладання визначника третього порядку по елементах третього рядка. Отже, мішаний добуток векторів дорівнює визначникові третього порядку, складеному з координат векторів, що перемножуються.
|
|||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 471; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.32.252 (0.006 с.) |

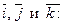
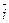
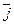
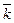

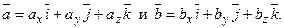 Знайдемо векторний добуток цих векторів, перемножуючи їх як багаточлени (згідно властивостей векторного добутку):
Знайдемо векторний добуток цих векторів, перемножуючи їх як багаточлени (згідно властивостей векторного добутку):
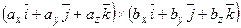



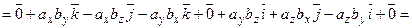
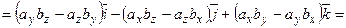
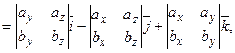
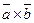
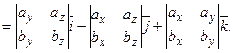 (3.1)
(3.1)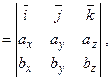 (3.2)
(3.2) ║
║  , то
, то  (і навпаки), тобто
(і навпаки), тобто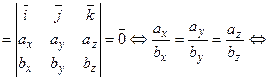
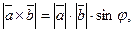 тобто
тобто 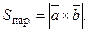 а тому
а тому 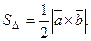
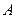 прикладена сила
прикладена сила 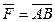 і нехай
і нехай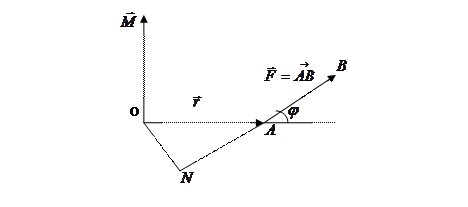
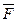 відносно точки
відносно точки 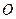 називається вектор
називається вектор 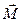 , що проходить через точку О і:
, що проходить через точку О і: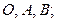

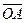 і
і 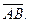

 точки М твердого тіла, що обертається
точки М твердого тіла, що обертається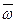 навколо нерухомої осі, визначається формулою Ейлера
навколо нерухомої осі, визначається формулою Ейлера 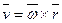 ; де
; де 
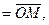 де
де
 і
і 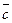 , складений в такий спосіб:
, складений в такий спосіб: 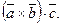 Тут перші два вектори перемножуються векторно, а їхній результат скалярно на третій вектор. Такий добуток називається векторно-скалярним, або мішаним, добутком трьох векторів. Мішаний добуток являє собою деяке число.
Тут перші два вектори перемножуються векторно, а їхній результат скалярно на третій вектор. Такий добуток називається векторно-скалярним, або мішаним, добутком трьох векторів. Мішаний добуток являє собою деяке число. (див. рис. 21.).
(див. рис. 21.).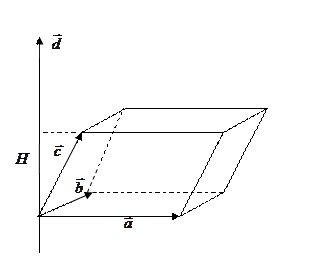

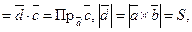 де
де 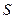 - площа паралелограма, побудованого на векторах
- площа паралелограма, побудованого на векторах 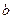 ,
, 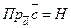 для правої трійки векторів і
для правої трійки векторів і 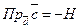 для лівої, де
для лівої, де 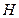 - висота паралелепіпеда. Одержуємо:
- висота паралелепіпеда. Одержуємо: 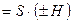 , тобто
, тобто 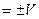 , де V – об'єм паралелепіпеда, утвореного векторами
, де V – об'єм паралелепіпеда, утвореного векторами 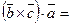
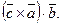
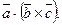
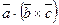
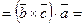
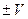 . Знак у правій частині цих рівностей беремо той самий, тому що трійки векторів
. Знак у правій частині цих рівностей беремо той самий, тому що трійки векторів  - однієї орієнтації. Отже,
- однієї орієнтації. Отже, 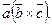 Це дозволяє записувати мішаний добуток векторів
Це дозволяє записувати мішаний добуток векторів  у виді
у виді  без знаків векторного, скалярного множення.
без знаків векторного, скалярного множення.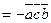 ,
, 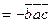 ,
, 
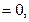 то
то 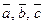 - компланарні.
- компланарні.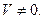 Але тому що
Але тому що 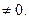 Це суперечить умові:
Це суперечить умові: 
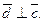 Тому
Тому  тобто
тобто 
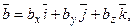
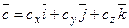 . Знайдемо їхній мішаний добуток, використовуючи вираження в координатах для векторного і скалярного добутку:
. Знайдемо їхній мішаний добуток, використовуючи вираження в координатах для векторного і скалярного добутку: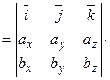
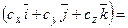
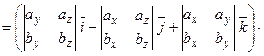
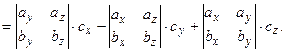 (4.1)
(4.1)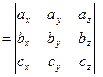 (4.2)
(4.2)


