
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Властивості скалярного добутку.Содержание книги Поиск на нашем сайте
1. Скалярний добуток володіє переставною властивістю: □ 2. Скалярний добуток має сполучну властивість щодо скалярного множина: □ 3. Скалярний добуток має розподільну властивість: □ 4. Скалярний квадрат вектора дорівнює квадратові його довжини: □ Зокрема: Якщо вектор Приклад 2.1. Знайти довжину вектора ○ 5. Якщо вектори □ Тому що Зокрема: Вираження скалярного добутку через координати. Нехай задані два вектори
Знайдемо скалярний добуток векторів, перемножуючи їх як многочлени (що законно в силу властивостей лінійності скалярного добутку) і користуючись таблицею скалярного добутку векторів
тобто
Отже, скалярний добуток векторів дорівнює сумі добутків їхніх однойменних координат. Приклад 2.2. Довести, що діагоналі чотирикутника, заданого координатами вершин ○ Знайдемо вектори
Звідси випливає, що Деякі застосування скалярного добутку. Кут між векторами Знаходження кута
Звідси випливає умова перпендикулярності ненульових векторів
Проекція вектора на заданий напрямок Знаходження проекції вектора
Робота постійної сили Нехай матеріальна точка переміщається прямолінійно з положення З фізики відомо, що робота сили
рис. 14. Таким чином, робота постійної сили при прямолінійному переміщенні її точки прикладання дорівнює скалярному добуткові вектора сили на вектор переміщення.
Приклад 2.3. Обчислити роботу, зроблену силою ○ Знаходимо
Кут
Тема 2.3. Векторний добуток вектора і його властивості. Означення векторного добутку. Три не компланарних вектори
рис.15. Ø Векторним добутком вектора 1) перпендикулярний векторам 2) має довжину, чисельно рівну площі паралелограма, побудованого на векторах
3) вектори
       
рис. 16. рис.17. Векторний добуток позначається
Властивості векторного добутку. 1. При перестановці співмножників векторний добуток змінює знак, тобто □ Вектори 2. Векторний добуток має сполучну властивість щодо скалярного множника, тобто
рис.18. □ Нехай
і
Тому 3. Два ненульових вектори □ Якщо Якщо ж v Зокрема, 4. Векторний добуток має розподільну властивість:
Приймемо без доведення.
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 633; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.16.208 (0.01 с.) |



 , а
, а 
 . І тому що
. І тому що  як добуток чисел і
як добуток чисел і 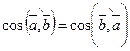 , то
, то 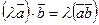 .
. .■
.■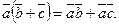
 .■
.■
 ■
■ .
. піднести скалярно в квадрат і потім добути корінь, то одержимо не первісний вектор, а його модуль
піднести скалярно в квадрат і потім добути корінь, то одержимо не первісний вектор, а його модуль  , тобто
, тобто  .
. якщо
якщо 


 .●
.● (ненульові) взаємно перпендикулярні, то їхній скалярний добуток дорівнює нулеві, тобто якщо
(ненульові) взаємно перпендикулярні, то їхній скалярний добуток дорівнює нулеві, тобто якщо  , то
, то 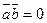 . Справедливо і обернене твердження: якщо
. Справедливо і обернене твердження: якщо 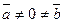 ,то
,то 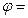
 то
то  Отже
Отже  Якщо ж
Якщо ж 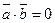 і
і  то
то 
 Звідси
Звідси  тобто
тобто 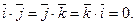
 і
і 
 :
: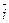
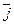


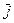
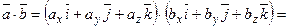





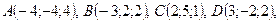 взаємно перпендикулярні.
взаємно перпендикулярні. і
і  , що лежать на діагоналях даного трикутника. Маємо:
, що лежать на діагоналях даного трикутника. Маємо:  і
і  Знайдемо скалярний добуток цих векторів:
Знайдемо скалярний добуток цих векторів: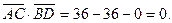
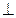
 взаємно перпендикулярні.●
взаємно перпендикулярні.● між ненульовими векторами
між ненульовими векторами  і
і 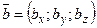 :
: тобто
тобто 


 може здійснюватися по формулі
може здійснюватися по формулі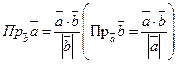 , тобто
, тобто 
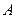 в положення
в положення  під дією постійної сили
під дією постійної сили 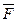 , що утворює кут
, що утворює кут  (див. рис. 14).
(див. рис. 14). дорівнює
дорівнює

 якщо точка її прикладання переміщається прямолінійно з положення
якщо точка її прикладання переміщається прямолінійно з положення  в положення
в положення 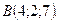 Під яким кутом до
Під яким кутом до  спрямована сила
спрямована сила  Стало бути,
Стало бути,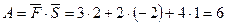 (од. роботи).
(од. роботи). тобто
тобто
 ●
● і
і 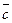 , узятих в зазначеному порядку, утворять праву трійку, якщо з кінця третього вектора
, узятих в зазначеному порядку, утворять праву трійку, якщо з кінця третього вектора 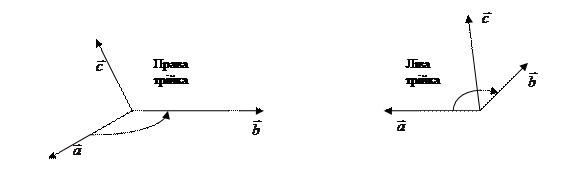








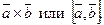 З означення векторного добутку безпосередньо випливають наступні співвідношення між ортами
З означення векторного добутку безпосередньо випливають наступні співвідношення між ортами 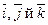 (див. рис.17):
(див. рис.17):
 (див. рис. 18).
(див. рис. 18).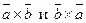 колінеарні, мають однакові модулі (площа паралелограма залишається незмінної), але протилежно спрямовані (трійки
колінеарні, мають однакові модулі (площа паралелограма залишається незмінної), але протилежно спрямовані (трійки  протилежної орієнтації). Стало бути,
протилежної орієнтації). Стало бути, 

 . Вектор
. Вектор  перпендикулярний векторам
перпендикулярний векторам  Вектор
Вектор  також перпендикулярний векторам
також перпендикулярний векторам  лежать в одній площині). Виходить вектори
лежать в одній площині). Виходить вектори  колінеарні. Очевидно, що і напрямку їх збігаються. Мають однакову довжину:
колінеарні. Очевидно, що і напрямку їх збігаються. Мають однакову довжину:
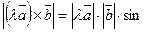
 =
= 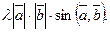
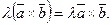 Аналогічно доводиться при
Аналогічно доводиться при  ■
■
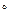 або 180
або 180 

 , то
, то  Але тоді
Але тоді  або
або  , тобто
, тобто 




