Замена переменной и интегрирование по частям под знаком неопределённого интеграла.
Первообразная и неопределённый интеграл. Таблица основных неопределённых интегралов.
Функция F(x) наз. первообразной для функции f(x) на интервале (a,b), если F(x) дифференцируема на [a,b] и  . Множество всех первообразных для данной ф-ции наз. неопределенным интегралом (НИ): . Множество всех первообразных для данной ф-ции наз. неопределенным интегралом (НИ):  . Свойства НИ: . Свойства НИ:  , , 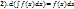 , , 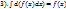
Таблица интегралов: 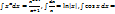
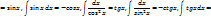
 , ,  , ,  , , 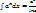 , ,  , ,  , ,  , ,  , ,  . Доп. св-ва НИ: . Доп. св-ва НИ:  , , 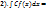
 . .  , , 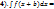
 , , 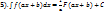 . .
Замена переменной и интегрирование по частям под знаком неопределённого интеграла.
 , ,  , t – новый аргумент; имеет обратную: t=ψ(x), , t – новый аргумент; имеет обратную: t=ψ(x),  . .
 , f(x)- произвольная ф-ция , f(x)- произвольная ф-ция  . .
Интегрирование по частям:  . Отметим, что метод применим к интегралам: . Отметим, что метод применим к интегралам:  и к инт-ам, содержащим обратные триг. ф-ции. Если подинт. выражение содержит многочлен, то этот многочлен берется за u, все ост. – dv. Если подинт. выражние содержит arcsin, arccos, т.е. трансценд. ф-ции, то эта ф-ция выбирается в кач. u, то же самое относится и к степеням трансц. ф-ции. Если встречается многочлен и тр. ф-ция, то u=многочлен. и к инт-ам, содержащим обратные триг. ф-ции. Если подинт. выражение содержит многочлен, то этот многочлен берется за u, все ост. – dv. Если подинт. выражние содержит arcsin, arccos, т.е. трансценд. ф-ции, то эта ф-ция выбирается в кач. u, то же самое относится и к степеням трансц. ф-ции. Если встречается многочлен и тр. ф-ция, то u=многочлен.
3). Интегрирование дробей вида: 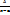 ; ;  ; ;  ; ;  , где , где  . .
1).  , 2). , 2).  , 3). , 3).  . .
4).  , последний инт-л по рекуррентной ф-ле приведется к интегралу , последний инт-л по рекуррентной ф-ле приведется к интегралу  : :  . .
4). Интегралы вида:  и и  . .
 этот инт-л можно привести к инт-лу от рациональной ф-ции, введя замену: этот инт-л можно привести к инт-лу от рациональной ф-ции, введя замену:  , q – наименьший общий знаменатель дробей: , q – наименьший общий знаменатель дробей:  . .
 инт-л приводится к инт-лу от рац. ф-ции подстановкой: инт-л приводится к инт-лу от рац. ф-ции подстановкой:  , s-наименьший общий знаменатель дробей: , s-наименьший общий знаменатель дробей:  . .
5). Интегралы вида:  , ,  . .
 . .
 . Последний инт-л был уже рассмотрен. . Последний инт-л был уже рассмотрен.
6). Интегралы вида:  , ,  . .
Выделяем полный квадрат в подкоренном выражении, чтобы привести инт-л к табличному:  . .
Пример:  . .
7). Интегралы вида:  . .
Тригонометрические подстановки при нахождении неопределённых интегралов.
I). 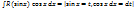
II). 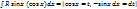
III).  , т.о. придем к инт-лу рац. ф-ции. , т.о. придем к инт-лу рац. ф-ции.
IV). Если подинт. ф-ция зависит только от tgx (или ее можно привести к такому виду), то: tgx=t.
V). Если sin и cos в четных степенях, то tgx=t,  , ,  . .
VI).  . .
 . .
 . Для нахождения каждого из интегралов с такими ф-лами используются эти преобразованиями. . Для нахождения каждого из интегралов с такими ф-лами используются эти преобразованиями.
VII).  . .
VIII). 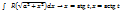
IX).  . .
Интегрирование дифференциальных биномов.
 рац. числа. П.А. Чебышев показал, что этот инт-л может быть выражен в простых ф-циях в 3-х случаях: рац. числа. П.А. Чебышев показал, что этот инт-л может быть выражен в простых ф-циях в 3-х случаях:
1.p-целое число -> x=  , s-общий знам. m и n. , s-общий знам. m и n.
2.  – целое число: – целое число:  , q – знаменатель др. p. , q – знаменатель др. p.
3.  – целое число: – целое число:  , q – знаменатель др. p. , q – знаменатель др. p.
 10). Понятие определённого интеграла, основные свойства определённого интеграла, его вычисление. 10). Понятие определённого интеграла, основные свойства определённого интеграла, его вычисление.
Криволинейная трапеция – фигура, ограниченная линиями. y=f(x), x=0, x=a, x=b. Подсчитаем S криволин. трап. хотя бы прближенно: 1). отрезок [a,b] разобьем точками деления  =b. =b. 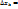
  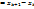 . 2). внутри кажд. отрезка . 2). внутри кажд. отрезка  произвольным образом выберем т-ку произвольным образом выберем т-ку  и проведем к ней ┴ до пересечения с дугой AB. и проведем к ней ┴ до пересечения с дугой AB.  - интегральная сумма. Тогда площ. всей криволинейной трапеции: - интегральная сумма. Тогда площ. всей криволинейной трапеции: 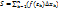 , , 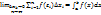 если этот предел сущ-т и не зависит от способа разбиения отрезка [a,b] на части, ни от выбора точек если этот предел сущ-т и не зависит от способа разбиения отрезка [a,b] на части, ни от выбора точек  в кажд. части, то он наз-ся определенным интегралом от ф-ции f(x)dx на отрезке [a,b]. Т.о. с геометрич. точки зрения введенный интеграл, представляет собой S криволин. трапеции: в кажд. части, то он наз-ся определенным интегралом от ф-ции f(x)dx на отрезке [a,b]. Т.о. с геометрич. точки зрения введенный интеграл, представляет собой S криволин. трапеции:  . Теорема 1. Если ф-ция f(x) непрерывна на [a,b], то она интегрируема на нем. По определению: . Теорема 1. Если ф-ция f(x) непрерывна на [a,b], то она интегрируема на нем. По определению:  . Основные св-ва ОИ (опред. инт-л): 1. . Основные св-ва ОИ (опред. инт-л): 1.  , 2. , 2. 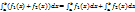 , 3. если на [a,b] 2 непрерывных ф-ции f(x) и , 3. если на [a,b] 2 непрерывных ф-ции f(x) и  удовлетворяют удовлетворяют  , то , то  , 4. если m и M есть соответственно наименьшее и наибольшее значения ф-ции f(x) на [a,b], M(b-a) , 4. если m и M есть соответственно наименьшее и наибольшее значения ф-ции f(x) на [a,b], M(b-a)  , 5. ТЕОРЕМА О СРЕДНЕМ: если f(x) интегрируема на [a,b], то внутри этого отрезка, то внутри [a,b] есть точка , 5. ТЕОРЕМА О СРЕДНЕМ: если f(x) интегрируема на [a,b], то внутри этого отрезка, то внутри [a,b] есть точка  : :  , ,  – среднее значение ф-ции f(x) на [a,b]. – среднее значение ф-ции f(x) на [a,b].  – S прямоуг. тр., основание кот. явл-ся ab, а высотой – S прямоуг. тр., основание кот. явл-ся ab, а высотой  . .
6. для любых точек a,b,c имеет место быть равенство:  .рис-> .рис->
7.если f(x) –четная ф-ция, то  . .
8.если f(x) – нечетная ф-ция, то  . .
Вычисление ОИ. Ф-ла Ньютога-Лейбница. Интеграл с переменным верхним пределом:  . Теорема: производная от инт-ла с переменным верхним пределом = подинт. ф-ции, в кот. вместо переменной интегрирования подставлено значения верхнего предела. На основании этой теоремы получили ф-лу, дающую возможность вычислить ОИ (эта ф-ла устанавливает связь между НИ и ОИ). Пусть есть . Теорема: производная от инт-ла с переменным верхним пределом = подинт. ф-ции, в кот. вместо переменной интегрирования подставлено значения верхнего предела. На основании этой теоремы получили ф-лу, дающую возможность вычислить ОИ (эта ф-ла устанавливает связь между НИ и ОИ). Пусть есть  – ф-ла Ньютона-Лейбница. – ф-ла Ньютона-Лейбница.  , ,  . .
Частные производные функции двух аргументов, их геометрический смысл.
Если ф-ция z=f(x,y) определена в нек. области D, тогда частное приращение  . Частная производная (1-го порядка) называется предел отношения частного приращения к приращению аргумента: . Частная производная (1-го порядка) называется предел отношения частного приращения к приращению аргумента:  . .
Геометрический смысл производных: частная производная ф-ции z=f(x,y) по х в т.( ) равна тангенсу угла с осью ОХ касательной к кривой, получаемой при пересечении с повехностью ) равна тангенсу угла с осью ОХ касательной к кривой, получаемой при пересечении с повехностью 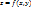 плоскости плоскости  , ,  , аналогично , аналогично  . .
Формула Грина.
Связь между 2-м инт-ом по обл. D и КРИ по границе L этой обл. уст-т ф-ла Остроградского-Грина. Пусть на плоскости Oxy задана область D, ограниченная кривой, пересекающейся с прямыми, || корд. осям не более чем в 2-х точках, т.е. область D – правильная.
Теорема: если P(x,y) и Q(x,y) непрерывны вместе со своими частными производными  и и  в обл. D, то имеет место ф-ла: в обл. D, то имеет место ф-ла:  , L – граница обл. D и интегр-ние кривой L производится в положит. напр. Эта ф-ла наз-ся Остроградского-Грина. , L – граница обл. D и интегр-ние кривой L производится в положит. напр. Эта ф-ла наз-ся Остроградского-Грина.
Замечание: ф-ла Грина справедлива и для произв. области, кот. можно разбить на конечное число правильных областей.
 Теорема: пусть Теорема: пусть  - ур. дуги AnB, а - ур. дуги AnB, а  – ур. дуги AmB. Найдем сначала – ур. дуги AmB. Найдем сначала  . По правилу вычисления 2-го инт-ла, имеем: . По правилу вычисления 2-го инт-ла, имеем:  . Аналогично док-ся, что . Аналогично док-ся, что  . Отсюда можно вывести ф-лу Грина. . Отсюда можно вывести ф-лу Грина.
Градиент.
Вектор, указывающий направление  , в кот. производная , в кот. производная  имеет наибольшее значение, наз-ся градиентом. Вектор, координатами кот. явл. значения частных производных ф-ции U(x,y,z) в точке M(x,y,z), наз-ют градиентом ф-ции и обозначают grad U, т.е. имеет наибольшее значение, наз-ся градиентом. Вектор, координатами кот. явл. значения частных производных ф-ции U(x,y,z) в точке M(x,y,z), наз-ют градиентом ф-ции и обозначают grad U, т.е. 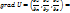
 . Отметим, что grad U есть вект. величина. Говорят: скал. поле U продолжает вект. поле градиента U. Теперь равенство . Отметим, что grad U есть вект. величина. Говорят: скал. поле U продолжает вект. поле градиента U. Теперь равенство  можно записать в виде: можно записать в виде:  , ,  , ,  - угол между вектором grad U и направлением - угол между вектором grad U и направлением  . Из последней ф-лы следует, что произв. по напр. достигает наиб. значения, когда . Из последней ф-лы следует, что произв. по напр. достигает наиб. значения, когда  , т.е. , т.е.  . Т.о., направление град. совпадает с напр. . Т.о., направление град. совпадает с напр.  , вдоль которого ф-ция (поле) меняется быстрее всего, т.е. градиент ф-ции указывает направление наибыстрейшего возрастаня ф-ции. Наибольшая скор. изменения ф-ции U в точке М равна: , вдоль которого ф-ция (поле) меняется быстрее всего, т.е. градиент ф-ции указывает направление наибыстрейшего возрастаня ф-ции. Наибольшая скор. изменения ф-ции U в точке М равна: 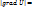
 . В этом сосотоит физ. смысл градиента. . В этом сосотоит физ. смысл градиента.
Св-ва градиента ф-ции: 1. град. направлен по нормали к пов-ти кровня, проходящей через данную точку. 2. grad(U+V)=gradU+gradV. 3. grad(cU)=cgradU, c=const. 4. grad(UV)=UgradV+VgradU. 5. grad  . 6. . 6.  . .
Замечание: эти св-ва градиента ф-ции справедливы и для плоского поля.
Поток векторного поля.
Пусть вект. поле образовано вектором  . Представим, что нек. пов-ть S нах-ся в потоке и пропускает жикость. Подсчитаем кол-во жидк., кот. протекает через пов-ть S. . Представим, что нек. пов-ть S нах-ся в потоке и пропускает жикость. Подсчитаем кол-во жидк., кот. протекает через пов-ть S.
Выберем опред сторону пов-ти S. пусть  - единичный вектор нормали к рассматриваемой стороне пов-ти S. Разобьем пов-ть на эл-ные площ-ки - единичный вектор нормали к рассматриваемой стороне пов-ти S. Разобьем пов-ть на эл-ные площ-ки  . Выберем в кажд. площ-ке т. . Выберем в кажд. площ-ке т.  и вычислим зн-ния вектора скор. и вычислим зн-ния вектора скор.  в кажд. точке. Будем приближенно считать кажд. площ-ку плоской, а в кажд. точке. Будем приближенно считать кажд. площ-ку плоской, а  пост. по модулю и одинаково направленным в кажд. т-ке площ-ки. Тогда за ед. вр. через пост. по модулю и одинаково направленным в кажд. т-ке площ-ки. Тогда за ед. вр. через  протекает кол-во жидк., протекает кол-во жидк.,  , где , где  - площ. i-ой площ-ки, - площ. i-ой площ-ки,  - высота i-ого цилиндра с образующей - высота i-ого цилиндра с образующей  . Но . Но  явл-ся проекцией явл-ся проекцией  на нормаль на нормаль  : :  = =  , ,  - единичный вектор нормали к пов-ти в т. - единичный вектор нормали к пов-ти в т.  . След-но, общее кол-во жидк., протекающее через всю пов-ть S за ед. вр., найдем вычислив сумму . След-но, общее кол-во жидк., протекающее через всю пов-ть S за ед. вр., найдем вычислив сумму  . .
Независимо от физ. смысла поля  полученный инт-л наз-ют потоком вект. поля. полученный инт-л наз-ют потоком вект. поля.
Потоком вект. поля  через пов-ть S – инт-л по пов-ти от скал. произв. вектора поля на ед. вектор нормали к поверхности, т.е.: через пов-ть S – инт-л по пов-ти от скал. произв. вектора поля на ед. вектор нормали к поверхности, т.е.:  . .
Т.к.  , где , где  - проекции вектора - проекции вектора  на соответств. коорд. оси, то поток вектора: на соответств. коорд. оси, то поток вектора: 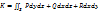 . Поток К вектора . Поток К вектора  есть скал. вел-на. Вел-на К = объему жидк., кот. протекает через пов-ть S за ед. вр. В этом состоит физ.смысл потока. есть скал. вел-на. Вел-на К = объему жидк., кот. протекает через пов-ть S за ед. вр. В этом состоит физ.смысл потока.
 Случай, когда пов-ть замкн. и огран-ет нек. объем V. Тогда поток вектора запис-ся: Случай, когда пов-ть замкн. и огран-ет нек. объем V. Тогда поток вектора запис-ся:  . В эт. случае за напр. вектора . В эт. случае за напр. вектора  обычно берут напр. внешней нормали и говорят о потоке изнутри пов-ти S. Если вект. поле обычно берут напр. внешней нормали и говорят о потоке изнутри пов-ти S. Если вект. поле  есть поле скоростей текущей жидкости, то величина потока К через замкн. пов-ть дает разность между кол-ом жидк-ти, вытек-щей из обл. V и втекающей в нее в ед. вр. (в точках пов-ти S, где вект. линии выходят из объема V, внешняя нормаль образует с вект-ом есть поле скоростей текущей жидкости, то величина потока К через замкн. пов-ть дает разность между кол-ом жидк-ти, вытек-щей из обл. V и втекающей в нее в ед. вр. (в точках пов-ти S, где вект. линии выходят из объема V, внешняя нормаль образует с вект-ом  острый угол и острый угол и  ; в точках, где вект. линии входят в объем, ; в точках, где вект. линии входят в объем,  ). ).
При этом если K>0, то из обл-ти V вытекает больше жидкости, чем в нее втекает. Это озн-ет, что внутри обл. имеются доп. ист-ки. Если К<0, то внутри обл. V есть стоки, поглощающие избыток жидкости. Если К=0, то из обл. V вытекает столько же жидк., сколько в нее втекает в ед. вр.; внутри обл. либо нет ни ист-ов, ни ст-ов, либо они таковы, что их действие взаимно компенсируется.
Пример: найти поток вект-ра  через верхнюю сторону треугольника, полученного при перес-нии плоскости 3x+6y-2z-6=0 с коорд. плоскостями. Решение: через верхнюю сторону треугольника, полученного при перес-нии плоскости 3x+6y-2z-6=0 с коорд. плоскостями. Решение:  . Нормаль к верхней стороне треуг. образует с осью Ox тупой угол, Oy – тупой, Oz – острый. . Нормаль к верхней стороне треуг. образует с осью Ox тупой угол, Oy – тупой, Oz – острый.  , на верхней стороне , на верхней стороне  , поэтому надо выбрать знак -; получим: , поэтому надо выбрать знак -; получим:  . Итак, . Итак, 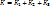 . Находим их: . Находим их:  . .  . . 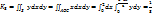 . .  . .
43. Формула Остроградского.
Используя понятия потока и дивергенции вект. поля, запишем ф-лу Остроградского-Гаусса: 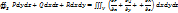 . Рассматривая обл. V, ограниченную замкн. пов-тью S, в вект. поле . Рассматривая обл. V, ограниченную замкн. пов-тью S, в вект. поле  , можно утв-ть, что левая часть ф-лы Остроградского есть поток вектора , можно утв-ть, что левая часть ф-лы Остроградского есть поток вектора  через пов-ть S; подынтегр. ф-ция правой чати ф-лы есть дивергенция вектора через пов-ть S; подынтегр. ф-ция правой чати ф-лы есть дивергенция вектора  . След-но ф-ла Остроградского может выглядеть так: . След-но ф-ла Остроградского может выглядеть так:  (встречается чаще всего). Ф-ла Остроградского-Гаусса означает, что поток вект. поля через замкн. пов-ть S (в напр. внешней нормали, т.е. изнутри) равен 3-ому инт-лу от див. этого поля по объему V, ограниченному данной пов-тью. Используя ф-лу (встречается чаще всего). Ф-ла Остроградского-Гаусса означает, что поток вект. поля через замкн. пов-ть S (в напр. внешней нормали, т.е. изнутри) равен 3-ому инт-лу от див. этого поля по объему V, ограниченному данной пов-тью. Используя ф-лу  , можно дать другое определение дивергенции вект. поля , можно дать другое определение дивергенции вект. поля  в точке М. в точке М.
По теореме о среднем для 3-ного инт-ла имеем:  , ,  – нек. (средняя) точка области V. Тогда ф-лу можно переписать: – нек. (средняя) точка области V. Тогда ф-лу можно переписать:  . Тогда: . Тогда:  . Пусть пов-ть S стягивается в точку. Тогда . Пусть пов-ть S стягивается в точку. Тогда  и мы получим выр-ние для и мы получим выр-ние для  в точке М: в точке М:  . .
 44. Формула Стокса. 44. Формула Стокса.
Пусть  - граница этой пов-ти (нарисуй!!!). Пусть всякая прямая || оси Oz пересекает пов-ть в одной точке. Пусть в кажд. точке пов-ти определен единичный вектор нормали: - граница этой пов-ти (нарисуй!!!). Пусть всякая прямая || оси Oz пересекает пов-ть в одной точке. Пусть в кажд. точке пов-ти определен единичный вектор нормали: 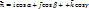 . В кажд. точке пов-ти определен вектор . В кажд. точке пов-ти определен вектор  . При указанных условиях имеет место так называемая ф-ла Стокса: . При указанных условиях имеет место так называемая ф-ла Стокса:  . .  . Этот инт-л наз-ся циркуляцией вект-ра . Этот инт-л наз-ся циркуляцией вект-ра  по этому контуру. Итак циркуляция вект. по этому контуру. Итак циркуляция вект.  по границе λ пространственной обл. σ равна потоку вихря векторя по границе λ пространственной обл. σ равна потоку вихря векторя  по самой пов-ти σ, причем направление обхода контура должно быть согласовано с ориентацией пов-ти. по самой пов-ти σ, причем направление обхода контура должно быть согласовано с ориентацией пов-ти. 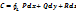 -еще один способ выч-ния циркуляции вектора -еще один способ выч-ния циркуляции вектора  по нек. контуру. по нек. контуру.
Оператор Гамильтона.
Действия взятия градиента, дивергенции и ротора наз-ся векторными операциями 1-го порядка (в них уч. 1-ые произв). Их удобно записывать с пом. оператора Гамельтона:  . Применяя опретор Гамильтона, получим дифф. операции 1-го порядка: . Применяя опретор Гамильтона, получим дифф. операции 1-го порядка:
1.  . .
2.  . .
3.  . .
Оператор Лапласа.
Оператор Лпласа – дифф. оператор, действующий в лин. простр-ве гладких ф-ций и обозначаемый символом  . Ф-ции F он ставит в соответствие ф-цию: . Ф-ции F он ставит в соответствие ф-цию:  . Оператор Лапласа . Оператор Лапласа  послед-ному взятию градиента и дивергенции послед-ному взятию градиента и дивергенции  , т.о. значение оператора Лапласа в точке может быть истолковано как плотность источников (стоков) потенциального , т.о. значение оператора Лапласа в точке может быть истолковано как плотность источников (стоков) потенциального 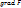 в этой точке. В декартовой системе координат оператор Лапласа часто обозначается следующим образом в этой точке. В декартовой системе координат оператор Лапласа часто обозначается следующим образом  , то есть в виде скалярного произведения оператора набла на себя. , то есть в виде скалярного произведения оператора набла на себя.
Первообразная и неопределённый интеграл. Таблица основных неопределённых интегралов.
Функция F(x) наз. первообразной для функции f(x) на интервале (a,b), если F(x) дифференцируема на [a,b] и  . Множество всех первообразных для данной ф-ции наз. неопределенным интегралом (НИ): . Множество всех первообразных для данной ф-ции наз. неопределенным интегралом (НИ):  . Свойства НИ: . Свойства НИ:  , , 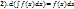 , , 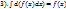
Таблица интегралов: 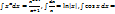
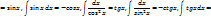
 , ,  , ,  , , 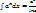 , ,  , ,  , ,  , ,  , ,  . Доп. св-ва НИ: . Доп. св-ва НИ:  , , 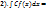
 . .  , , 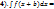
 , , 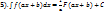 . .
Замена переменной и интегрирование по частям под знаком неопределённого интеграла.
 , ,  , t – новый аргумент; имеет обратную: t=ψ(x), , t – новый аргумент; имеет обратную: t=ψ(x),  . .
 , f(x)- произвольная ф-ция , f(x)- произвольная ф-ция  . .
Интегрирование по частям:  . Отметим, что метод применим к интегралам: . Отметим, что метод применим к интегралам:  и к инт-ам, содержащим обратные триг. ф-ции. Если подинт. выражение содержит многочлен, то этот многочлен берется за u, все ост. – dv. Если подинт. выражние содержит arcsin, arccos, т.е. трансценд. ф-ции, то эта ф-ция выбирается в кач. u, то же самое относится и к степеням трансц. ф-ции. Если встречается многочлен и тр. ф-ция, то u=многочлен. и к инт-ам, содержащим обратные триг. ф-ции. Если подинт. выражение содержит многочлен, то этот многочлен берется за u, все ост. – dv. Если подинт. выражние содержит arcsin, arccos, т.е. трансценд. ф-ции, то эта ф-ция выбирается в кач. u, то же самое относится и к степеням трансц. ф-ции. Если встречается многочлен и тр. ф-ция, то u=многочлен.
3). Интегрирование дробей вида: 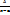 ; ;  ; ;  ; ;  , где , где  . .
1).  , 2). , 2).  , 3). , 3).  . .
4).  , последний инт-л по рекуррентной ф-ле приведется к интегралу , последний инт-л по рекуррентной ф-ле приведется к интегралу  : :  . .
4). Интегралы вида:  и и  . .
 этот инт-л можно привести к инт-лу от рациональной ф-ции, введя замену: этот инт-л можно привести к инт-лу от рациональной ф-ции, введя замену:  , q – наименьший общий знаменатель дробей: , q – наименьший общий знаменатель дробей:  . .
 инт-л приводится к инт-лу от рац. ф-ции подстановкой: инт-л приводится к инт-лу от рац. ф-ции подстановкой:  , s-наименьший общий знаменатель дробей: , s-наименьший общий знаменатель дробей:  . .
5). Интегралы вида:  , ,  . .
 . .
 . Последний инт-л был уже рассмотрен. . Последний инт-л был уже рассмотрен.
6). Интегралы вида:  , ,  . .
Выделяем полный квадрат в подкоренном выражении, чтобы привести инт-л к табличному:  . .
Пример:  . .
7). Интегралы вида:  . .
|



 . Множество всех первообразных для данной ф-ции наз. неопределенным интегралом (НИ):
. Множество всех первообразных для данной ф-ции наз. неопределенным интегралом (НИ):  . Свойства НИ:
. Свойства НИ:  ,
, 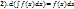 ,
, 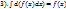
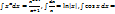
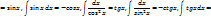
 ,
,  ,
,  ,
, 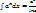 ,
,  ,
,  ,
,  ,
,  ,
,  . Доп. св-ва НИ:
. Доп. св-ва НИ:  ,
, 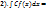
 .
.  ,
, 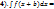
 ,
, 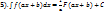 .
. ,
,  , t – новый аргумент; имеет обратную: t=ψ(x),
, t – новый аргумент; имеет обратную: t=ψ(x),  .
. , f(x)- произвольная ф-ция
, f(x)- произвольная ф-ция  .
. . Отметим, что метод применим к интегралам:
. Отметим, что метод применим к интегралам:  и к инт-ам, содержащим обратные триг. ф-ции. Если подинт. выражение содержит многочлен, то этот многочлен берется за u, все ост. – dv. Если подинт. выражние содержит arcsin, arccos, т.е. трансценд. ф-ции, то эта ф-ция выбирается в кач. u, то же самое относится и к степеням трансц. ф-ции. Если встречается многочлен и тр. ф-ция, то u=многочлен.
и к инт-ам, содержащим обратные триг. ф-ции. Если подинт. выражение содержит многочлен, то этот многочлен берется за u, все ост. – dv. Если подинт. выражние содержит arcsin, arccos, т.е. трансценд. ф-ции, то эта ф-ция выбирается в кач. u, то же самое относится и к степеням трансц. ф-ции. Если встречается многочлен и тр. ф-ция, то u=многочлен.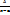 ;
;  ;
;  ;
;  , где
, где  .
. , 2).
, 2).  , 3).
, 3).  .
. , последний инт-л по рекуррентной ф-ле приведется к интегралу
, последний инт-л по рекуррентной ф-ле приведется к интегралу  :
:  .
. и
и  .
. этот инт-л можно привести к инт-лу от рациональной ф-ции, введя замену:
этот инт-л можно привести к инт-лу от рациональной ф-ции, введя замену:  , q – наименьший общий знаменатель дробей:
, q – наименьший общий знаменатель дробей:  .
. инт-л приводится к инт-лу от рац. ф-ции подстановкой:
инт-л приводится к инт-лу от рац. ф-ции подстановкой:  , s-наименьший общий знаменатель дробей:
, s-наименьший общий знаменатель дробей:  .
. ,
,  .
. .
. . Последний инт-л был уже рассмотрен.
. Последний инт-л был уже рассмотрен. ,
,  .
. .
. .
. .
.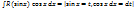
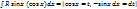
 , т.о. придем к инт-лу рац. ф-ции.
, т.о. придем к инт-лу рац. ф-ции. ,
,  .
. .
. .
. . Для нахождения каждого из интегралов с такими ф-лами используются эти преобразованиями.
. Для нахождения каждого из интегралов с такими ф-лами используются эти преобразованиями. .
.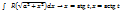
 .
. рац. числа. П.А. Чебышев показал, что этот инт-л может быть выражен в простых ф-циях в 3-х случаях:
рац. числа. П.А. Чебышев показал, что этот инт-л может быть выражен в простых ф-циях в 3-х случаях: , s-общий знам. m и n.
, s-общий знам. m и n. – целое число:
– целое число:  , q – знаменатель др. p.
, q – знаменатель др. p. – целое число:
– целое число:  , q – знаменатель др. p.
, q – знаменатель др. p. 10). Понятие определённого интеграла, основные свойства определённого интеграла, его вычисление.
10). Понятие определённого интеграла, основные свойства определённого интеграла, его вычисление. =b.
=b. 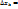


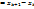 . 2). внутри кажд. отрезка
. 2). внутри кажд. отрезка  произвольным образом выберем т-ку
произвольным образом выберем т-ку  и проведем к ней ┴ до пересечения с дугой AB.
и проведем к ней ┴ до пересечения с дугой AB.  - интегральная сумма. Тогда площ. всей криволинейной трапеции:
- интегральная сумма. Тогда площ. всей криволинейной трапеции: 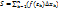 ,
, 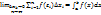 если этот предел сущ-т и не зависит от способа разбиения отрезка [a,b] на части, ни от выбора точек
если этот предел сущ-т и не зависит от способа разбиения отрезка [a,b] на части, ни от выбора точек  в кажд. части, то он наз-ся определенным интегралом от ф-ции f(x)dx на отрезке [a,b]. Т.о. с геометрич. точки зрения введенный интеграл, представляет собой S криволин. трапеции:
в кажд. части, то он наз-ся определенным интегралом от ф-ции f(x)dx на отрезке [a,b]. Т.о. с геометрич. точки зрения введенный интеграл, представляет собой S криволин. трапеции:  . Теорема 1. Если ф-ция f(x) непрерывна на [a,b], то она интегрируема на нем. По определению:
. Теорема 1. Если ф-ция f(x) непрерывна на [a,b], то она интегрируема на нем. По определению:  . Основные св-ва ОИ (опред. инт-л): 1.
. Основные св-ва ОИ (опред. инт-л): 1.  , 2.
, 2. 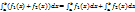 , 3. если на [a,b] 2 непрерывных ф-ции f(x) и
, 3. если на [a,b] 2 непрерывных ф-ции f(x) и  удовлетворяют
удовлетворяют  , то
, то  , 4. если m и M есть соответственно наименьшее и наибольшее значения ф-ции f(x) на [a,b], M(b-a)
, 4. если m и M есть соответственно наименьшее и наибольшее значения ф-ции f(x) на [a,b], M(b-a)  , 5. ТЕОРЕМА О СРЕДНЕМ: если f(x) интегрируема на [a,b], то внутри этого отрезка, то внутри [a,b] есть точка
, 5. ТЕОРЕМА О СРЕДНЕМ: если f(x) интегрируема на [a,b], то внутри этого отрезка, то внутри [a,b] есть точка  :
:  ,
,  – среднее значение ф-ции f(x) на [a,b].
– среднее значение ф-ции f(x) на [a,b].  – S прямоуг. тр., основание кот. явл-ся ab, а высотой
– S прямоуг. тр., основание кот. явл-ся ab, а высотой  .рис->
.рис-> .
. .
. . Теорема: производная от инт-ла с переменным верхним пределом = подинт. ф-ции, в кот. вместо переменной интегрирования подставлено значения верхнего предела. На основании этой теоремы получили ф-лу, дающую возможность вычислить ОИ (эта ф-ла устанавливает связь между НИ и ОИ). Пусть есть
. Теорема: производная от инт-ла с переменным верхним пределом = подинт. ф-ции, в кот. вместо переменной интегрирования подставлено значения верхнего предела. На основании этой теоремы получили ф-лу, дающую возможность вычислить ОИ (эта ф-ла устанавливает связь между НИ и ОИ). Пусть есть  – ф-ла Ньютона-Лейбница.
– ф-ла Ньютона-Лейбница.  ,
,  .
. . Частная производная (1-го порядка) называется предел отношения частного приращения к приращению аргумента:
. Частная производная (1-го порядка) называется предел отношения частного приращения к приращению аргумента:  .
. ) равна тангенсу угла с осью ОХ касательной к кривой, получаемой при пересечении с повехностью
) равна тангенсу угла с осью ОХ касательной к кривой, получаемой при пересечении с повехностью 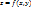 плоскости
плоскости  ,
,  , аналогично
, аналогично  .
. и
и  в обл. D, то имеет место ф-ла:
в обл. D, то имеет место ф-ла:  , L – граница обл. D и интегр-ние кривой L производится в положит. напр. Эта ф-ла наз-ся Остроградского-Грина.
, L – граница обл. D и интегр-ние кривой L производится в положит. напр. Эта ф-ла наз-ся Остроградского-Грина. Теорема: пусть
Теорема: пусть  - ур. дуги AnB, а
- ур. дуги AnB, а  – ур. дуги AmB. Найдем сначала
– ур. дуги AmB. Найдем сначала  . По правилу вычисления 2-го инт-ла, имеем:
. По правилу вычисления 2-го инт-ла, имеем:  . Аналогично док-ся, что
. Аналогично док-ся, что  . Отсюда можно вывести ф-лу Грина.
. Отсюда можно вывести ф-лу Грина. , в кот. производная
, в кот. производная  имеет наибольшее значение, наз-ся градиентом. Вектор, координатами кот. явл. значения частных производных ф-ции U(x,y,z) в точке M(x,y,z), наз-ют градиентом ф-ции и обозначают grad U, т.е.
имеет наибольшее значение, наз-ся градиентом. Вектор, координатами кот. явл. значения частных производных ф-ции U(x,y,z) в точке M(x,y,z), наз-ют градиентом ф-ции и обозначают grad U, т.е. 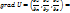
 . Отметим, что grad U есть вект. величина. Говорят: скал. поле U продолжает вект. поле градиента U. Теперь равенство
. Отметим, что grad U есть вект. величина. Говорят: скал. поле U продолжает вект. поле градиента U. Теперь равенство  можно записать в виде:
можно записать в виде:  ,
,  ,
,  - угол между вектором grad U и направлением
- угол между вектором grad U и направлением  , т.е.
, т.е.  . Т.о., направление град. совпадает с напр.
. Т.о., направление град. совпадает с напр. 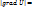
 . В этом сосотоит физ. смысл градиента.
. В этом сосотоит физ. смысл градиента. . 6.
. 6.  .
. . Представим, что нек. пов-ть S нах-ся в потоке и пропускает жикость. Подсчитаем кол-во жидк., кот. протекает через пов-ть S.
. Представим, что нек. пов-ть S нах-ся в потоке и пропускает жикость. Подсчитаем кол-во жидк., кот. протекает через пов-ть S. - единичный вектор нормали к рассматриваемой стороне пов-ти S. Разобьем пов-ть на эл-ные площ-ки
- единичный вектор нормали к рассматриваемой стороне пов-ти S. Разобьем пов-ть на эл-ные площ-ки  . Выберем в кажд. площ-ке т.
. Выберем в кажд. площ-ке т.  и вычислим зн-ния вектора скор.
и вычислим зн-ния вектора скор.  в кажд. точке. Будем приближенно считать кажд. площ-ку плоской, а
в кажд. точке. Будем приближенно считать кажд. площ-ку плоской, а  , где
, где  - площ. i-ой площ-ки,
- площ. i-ой площ-ки,  - высота i-ого цилиндра с образующей
- высота i-ого цилиндра с образующей  . Но
. Но  :
:  =
=  ,
,  .
. полученный инт-л наз-ют потоком вект. поля.
полученный инт-л наз-ют потоком вект. поля. .
. , где
, где  - проекции вектора
- проекции вектора 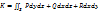 . Поток К вектора
. Поток К вектора  Случай, когда пов-ть замкн. и огран-ет нек. объем V. Тогда поток вектора запис-ся:
Случай, когда пов-ть замкн. и огран-ет нек. объем V. Тогда поток вектора запис-ся:  . В эт. случае за напр. вектора
. В эт. случае за напр. вектора  обычно берут напр. внешней нормали и говорят о потоке изнутри пов-ти S. Если вект. поле
обычно берут напр. внешней нормали и говорят о потоке изнутри пов-ти S. Если вект. поле  есть поле скоростей текущей жидкости, то величина потока К через замкн. пов-ть дает разность между кол-ом жидк-ти, вытек-щей из обл. V и втекающей в нее в ед. вр. (в точках пов-ти S, где вект. линии выходят из объема V, внешняя нормаль образует с вект-ом
есть поле скоростей текущей жидкости, то величина потока К через замкн. пов-ть дает разность между кол-ом жидк-ти, вытек-щей из обл. V и втекающей в нее в ед. вр. (в точках пов-ти S, где вект. линии выходят из объема V, внешняя нормаль образует с вект-ом  ; в точках, где вект. линии входят в объем,
; в точках, где вект. линии входят в объем,  ).
). через верхнюю сторону треугольника, полученного при перес-нии плоскости 3x+6y-2z-6=0 с коорд. плоскостями. Решение:
через верхнюю сторону треугольника, полученного при перес-нии плоскости 3x+6y-2z-6=0 с коорд. плоскостями. Решение:  . Нормаль к верхней стороне треуг. образует с осью Ox тупой угол, Oy – тупой, Oz – острый.
. Нормаль к верхней стороне треуг. образует с осью Ox тупой угол, Oy – тупой, Oz – острый.  , на верхней стороне
, на верхней стороне  , поэтому надо выбрать знак -; получим:
, поэтому надо выбрать знак -; получим:  . Итак,
. Итак, 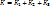 . Находим их:
. Находим их:  .
.  .
. 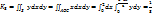 .
.  .
.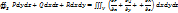 . Рассматривая обл. V, ограниченную замкн. пов-тью S, в вект. поле
. Рассматривая обл. V, ограниченную замкн. пов-тью S, в вект. поле  (встречается чаще всего). Ф-ла Остроградского-Гаусса означает, что поток вект. поля через замкн. пов-ть S (в напр. внешней нормали, т.е. изнутри) равен 3-ому инт-лу от див. этого поля по объему V, ограниченному данной пов-тью. Используя ф-лу
(встречается чаще всего). Ф-ла Остроградского-Гаусса означает, что поток вект. поля через замкн. пов-ть S (в напр. внешней нормали, т.е. изнутри) равен 3-ому инт-лу от див. этого поля по объему V, ограниченному данной пов-тью. Используя ф-лу  ,
,  – нек. (средняя) точка области V. Тогда ф-лу можно переписать:
– нек. (средняя) точка области V. Тогда ф-лу можно переписать:  . Тогда:
. Тогда:  . Пусть пов-ть S стягивается в точку. Тогда
. Пусть пов-ть S стягивается в точку. Тогда  и мы получим выр-ние для
и мы получим выр-ние для  в точке М:
в точке М:  .
. 44. Формула Стокса.
44. Формула Стокса. - граница этой пов-ти (нарисуй!!!). Пусть всякая прямая || оси Oz пересекает пов-ть в одной точке. Пусть в кажд. точке пов-ти определен единичный вектор нормали:
- граница этой пов-ти (нарисуй!!!). Пусть всякая прямая || оси Oz пересекает пов-ть в одной точке. Пусть в кажд. точке пов-ти определен единичный вектор нормали: 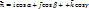 . В кажд. точке пов-ти определен вектор
. В кажд. точке пов-ти определен вектор  . При указанных условиях имеет место так называемая ф-ла Стокса:
. При указанных условиях имеет место так называемая ф-ла Стокса:  .
.  . Этот инт-л наз-ся циркуляцией вект-ра
. Этот инт-л наз-ся циркуляцией вект-ра  по этому контуру. Итак циркуляция вект.
по этому контуру. Итак циркуляция вект.  по границе λ пространственной обл. σ равна потоку вихря векторя
по границе λ пространственной обл. σ равна потоку вихря векторя 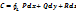 -еще один способ выч-ния циркуляции вектора
-еще один способ выч-ния циркуляции вектора  . Применяя опретор Гамильтона, получим дифф. операции 1-го порядка:
. Применяя опретор Гамильтона, получим дифф. операции 1-го порядка: .
. .
. .
. . Ф-ции F он ставит в соответствие ф-цию:
. Ф-ции F он ставит в соответствие ф-цию:  . Оператор Лапласа
. Оператор Лапласа  послед-ному взятию градиента и дивергенции
послед-ному взятию градиента и дивергенции  , т.о. значение оператора Лапласа в точке может быть истолковано как плотность источников (стоков) потенциального
, т.о. значение оператора Лапласа в точке может быть истолковано как плотность источников (стоков) потенциального 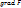 в этой точке. В декартовой системе координат оператор Лапласа часто обозначается следующим образом
в этой точке. В декартовой системе координат оператор Лапласа часто обозначается следующим образом  , то есть в виде скалярного произведения оператора набла на себя.
, то есть в виде скалярного произведения оператора набла на себя.


